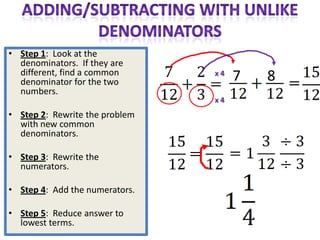
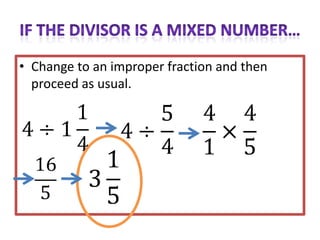
The document provides instructions and examples for performing various fraction operations, such as changing fractions to mixed numbers and improper fractions, reducing fractions, adding and subtracting fractions, multiplying and dividing fractions, and canceling common factors. Key steps are outlined for each type of fraction problem to demonstrate the procedure. Examples are included to illustrate how to apply the steps to calculate fraction problems.

1. • 1. GED Practice (Writing Decimals as
Fractions)
• 2. Basic Review of fractions
• 3. A/S/M/D Fractions

2. • At his job, Peter fills out a time sheet every Friday.
This week, Peter spent 27.5 hours out of 40 hours, or
0.6875 of his time, working on Project A.
• Which fraction is the best estimate of the time Peter
spent on Project A?
“seven tenths”
(1) 2/3
(2) 3/4
(3) 3/10
(4) 7/10
(5) 7/25

3. • Summary:
– Divide the denominator into the numerator
– Write the remainder as a fraction
•Example 1: Change to a mixed number.
4
•Step 1: Divide 3 into 14.
3) 14
- 12
2
•Step 2: Write the remainder (2) over the divisor
(3) to form the fraction part of the answer.

4. •Example 2: Change to a mixed number.
1
•Step 1: Divide 8 into 12.
8) 12
- 8
4
•Step 2: Write the remainder (4) over the divisor
(8) to form the fraction part of the answer.
•Step 3: Reduce the fraction

5. • Summary:
– Multiply the whole number by the denominator
– Add to the numerator
– Place over the current denominator
•Example 1: Change to an improper fraction.
•Step 1: Multiply the whole number by the
denominator .
•Step 2: Add the numerator to the product.
• Step 3: Write the answer over the denominator
to form the fraction part of the answer.

6. • Summary: Reducing changes the numbers in
a fraction, but it does not change the VALUE
of a fraction.
Example: Reduce
To reduce a fraction,
you divide both the •Step 1: Divide
numerator and both 14 and 16
denominator by a
by a number
number that goes
into them both that goes evenly
evenly. into both of
them.

7. • You will need to know how to set up fractions
and reduce them.
Example: John makes $800 a month. He pays $200 a
month to rent a room. What fraction of his income does
John pay for rent?
• Step 1: Find the whole.
Write it in the denominator.
• Step 2: Find the part. Write
it in the numerator.
• Step 3: Reduce.

8. • Summary: Reducing changes the numbers in
a fraction, but it does not change the VALUE
of a fraction.
•Step 1: Divide Example: Reduce
both 30 and 45
by a number
that goes evenly
into both of
them.

9. • Summary: Later when you add and subtract fractions,
you will often need to raise fractions to higher terms.
This is the opposite of reducing.
Example: Raise the fraction to higher terms by
finding the missing numerator.
•Step 1: Divide the 4
new numerator by the 6) 24
old denominator.
•Step 2: Multiply both
the old denominator
and numerator by 4.

10. • Summary: To compare fractions, you must have the
same denominators. Raise each fraction to higher
terms, then the new compare numerators.
Example: Which fraction is bigger,
•Step 1: Find a
common denominator ×7 21
for 5 and 7 and raise to 7
higher terms. ×7 5) 35
•Step 2: Look at the
numerators and
decide which one is
×5 25 5
×5 7) 35
bigger.

11. • Step 1: Look at the
denominators. If they are
different, find a common
denominator for the two
x4
7 8
numbers.
x4
• Step 2: Rewrite the problem
with new common
denominators.
• Step 3: Rewrite the
numerators.
• Step 4: Add the numerators.
• Step 5: Reduce answer to
lowest terms.

12. •Step 1: Find the Lowest ×3
Common Denominator 21
•Step 2: Add numerators ×3
×8 16
•Step 3: Change the
improper fraction to a
mixed number ×8
•Step 4: Add the whole
-24 13
number part of the
answer to the mixed number.

13. Step 1: Find a
common
denominator.
Step 2: Since you
×3 8 6 cannot take 7 from 6,
you must borrow
ONE from the whole
×3 number and add it to
the fraction.
Step 3: Subtract the
numerators, keep the
denominator.
Step 4: Subtract the
whole numbers.

14. • Step 1: Multiply the numerators together
• Step 2: Multiply the denominators together.
• Step 3: Reduce the answer if possible.
21

80

15. • To cancel, find a number that divides evenly
into the numerator of one fraction and the
denominator of the other.
1 2 •Step 1: Divide 3 and 15 by 3
2 •Step 2: Divide 4 and 8 by 4
•Step 3: Multiply the new
1 5
5 numerators and
denominators.

16. • A whole number can be written as a fraction
with a denominator of 1.
• Remember: a fraction of means to multiply.
Find ¾ of 24.
•Step 1: Write 24 as a fraction.
•Step 2: Divide 4 and 24 by 4.
•Step 3: Multiply across.
•Step 4: Change the improper
fraction to a whole number.

17. • Step 1: Change to an
improper
fraction.
• Step 2: Divide 4 and
6 by 2.
• Step 3: Multiply
across.
• Step 4: Change the
improper
fraction to a
mixed number.

18. • In division problems with fractions
or mixed numbers, you must invert
the divisor. The fraction ½ is the
reciprocal, or the inverse of the
improper fraction 2/1.

19. • Step 1: Write each number in fraction form.
• Step 2: Invert the divisor and change the
to a sign. (KSF!)
• Step 3: Follow the rules for multiplying
fractions.

20. • Change to an improper fraction and then
proceed as usual.