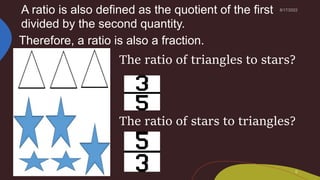
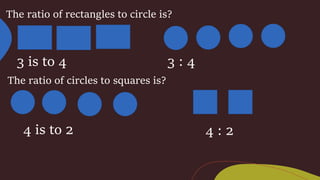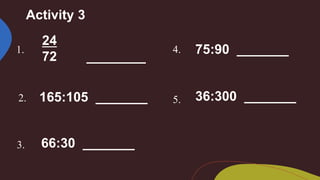
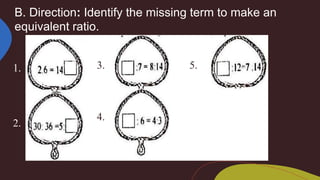
1. The document provides a lesson on ratios that teaches learners to visualize, identify, write, and simplify ratios. It includes examples of counting objects to write ratios and determining if ratios are equivalent. 2. Methods taught for finding equivalent ratios include cross multiplication and multiplying the means and extremes. Rules are given for simplifying ratios, including using the greatest common factor. 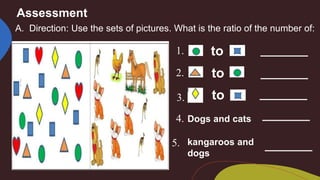3. The lesson emphasizes that ratios can be used in daily life, such as a cooking recipe, and provides an assessment with ratio questions and problems to simplify ratios.

1. Demostration
Lesson

2. Ratio the Easy Way
At the end of the lesson the learners should be able to:
1. Visualize the ratio of 2 given numbers (M5NS-Iih-122)
2. Identify and write equivalent ratios the ratio of 2 given
numbers (M5NS-Iih-124)
3. Express ratio in their simples form(M5NS-Iih-125)
4. Appreciate the importance of ratio number

3. Look at the picture below.
How many rectangles and
circles are there?
How many figures altogether?
3 rectangles
4 circles
7 figures all together

4. The ratio of rectangles to circle is?
3 is to 4 3 : 4
The ratio of circles to squares is?
4 is to 2 4 : 2

5. A ratio is a comparison of two different things or
numbers. We generally express the two numbers as a
ratio using colon (:)
3 : 4

6. The ratio of triangles to stars?
The ratio of stars to triangles?
A ratio is also defined as the quotient of the first
divided by the second quantity.
Therefore, a ratio is also a fraction.

7. Activity 1
Direction: Count the number of objects and write the ratio on the
blank provided.
1. 2.
3. 4.

8. 5.

9. Equivalent ratios (which are, in effect,
equivalent fractions) are two fractions that
express the same relationship between
numbers. We can create equivalent ratios by
multiplying or dividing both the numerator and
denominator of a given ratio by the same
number.

10. How to find an equivalent ratio?
To find an equivalent ratio, multiply or divide the numerator and
denominator of the given ratio by one counting number. It is the
same process as finding equivalent fractions.
By multiplying each ratio by the second number of the other
ratio you can determine if they are equivalent. Multiply both
numbers in the first ratio. For example, if the ratios are 3:5 and
9:15, multiply 3 by 15 and 5 by 15 to get 45:75.

11. Example 1
1.Determine whether the ratios 180 miles in 3 hours and 300 miles
in 5 hours are equivalent.
For 180, the GCF is 3.
3
For 300, the GCF is 5.
5
For 180 3 = 60
3 3 1
For 300 5 = 60
5 5 1
The simplest form of 180, is 60.
3 1
The simplest form of 300, is 60.
5 1
The ratios are equivalent since their simplest forms
are equal.

12. 2. Identify another ratio equal to the given ratios in Example 1, number 1.
To identify a ratio equal to a given ratio, simply multiply or divide the
numerator and denominator of the given ratio by one counting number.
*Note that counting numbers do not include zero.
a. 180 3 = 540
3 3 9
b. 300 2 = 600
5 2 10
c. 60 60 = 3600
1 60 60

13. Identifying equivalent ratio
A. Cross Multiplication Method
Example: Is 2:5 and 20:50 are equivalent ratios?
Express the ratios into fraction form.
2 20
5 50
2 X 50
100
20 X 5
100

14. B. Multiplication of Means and Extremes
Example : Are ratios 3:4 and 9:12
equivalent ratios?
3:4 = 9:12
3x12
36
9x4
36

15. Activity 2
1. 7:6 = (__):36
2. 5 40
6 (__)
3. (__) 1
35 7
4. 6:9 = 42:(__)
5. (__):8 = 14:28

16. Expresses ratios in their simplest form
To express ratios in its simplest form you can use the same method that is used
to simplify fractions. The two examples below show how to simplify ratios and
fractions by dividing the numbers by their greatest common factor (GCF).
Fraction Ratio
4
12
4:12
4 4
4= 1,2,4
12= 1,2,3,4,6,12
4
4
4:12
1
3
1
3

17. Let us learn some special rules to help us know how to simplify ratios.
Simplify 15:20
Ratio 15:20
What are the factors of 15? 1,3,5,15
What are the factors of 20? 1,2,4,5,10,20
What is the Greatest
Common Factor (G.C.F)?
5
Divide both terms by G.C.F 15 5 = 3
20 5 = 4
What is the simplest form of
the ratio?
3:4

18. Activity 3
1.
24
72 ________
2. 165:105 _______
3. 66:30 _______
4. 75:90 _______
5. 36:300 _______

19. What is a ratio?
What are the ways on how to find
the equivalent ratios?
What are the rules or step to help
us simplify ratio?

20. Ratio can not only be used in mathematics but
it can also be used in our daily lives like
cooking. Example when you make a pancake
for every cup of flour we need 2 cups of water.
This is easy to visualize as ratio of 1 cup of
flour to 2 cups of water.
Integration

21. Assessment
A. Direction: Use the sets of pictures. What is the ratio of the number of:
1. to ________
2. to
Dogs and cats
3.
________
________
4. ________
5. kangaroos and
dogs
________
to

22. B. Direction: Identify the missing term to make an
equivalent ratio.
1.
2.
3.
4.
5.

23. C. Read the questions carefully. Simplify your answer.
11. Daniel drew 9 triangles, 6 squares, and 12 stars. What is the ratio
of triangles to stars?
A. 9:12 B. 6:12 C. 3:4 D. 2:4
12. A group of grade 4 pupils has 8 boys and 24 girls. What is the
ratio of girls to all grade 4 pupils?
A. 4:8 B. 3:4 C. 8:24 D. 4:24
13. A group of kindergarten pupils has 15 boys and 12 girls. What is the
ratio of girls to boys?
A. 12:15 B. 4:5 C. 15:12 D. 5:4

24. 14.A drawing consists of 4 yellow mangoes to every 12 red apples.
What is the ratio of yellow mangoes to all fruits?
A. 4:12 B. 1:4 C. 12:4 D. 12:16
15. A Grade 5 EsP club has 21 members, of which 13 are males
and the rest are females. What is the ratio of females to all Grade 5
EsP club members?
A. 4:12 B. 8:21 C. 12:4 D. 12:16

25. D. Write the given ratios in simplest form:
16. 5 kilometers to 40 kilometers __________
17. 8 liters to 24 liters __________
18. 20 minutes to 50 minutes ________
19. 21 marbles to 35 marbles ________
20. 60 rubber bands to 90 rubber bands ________