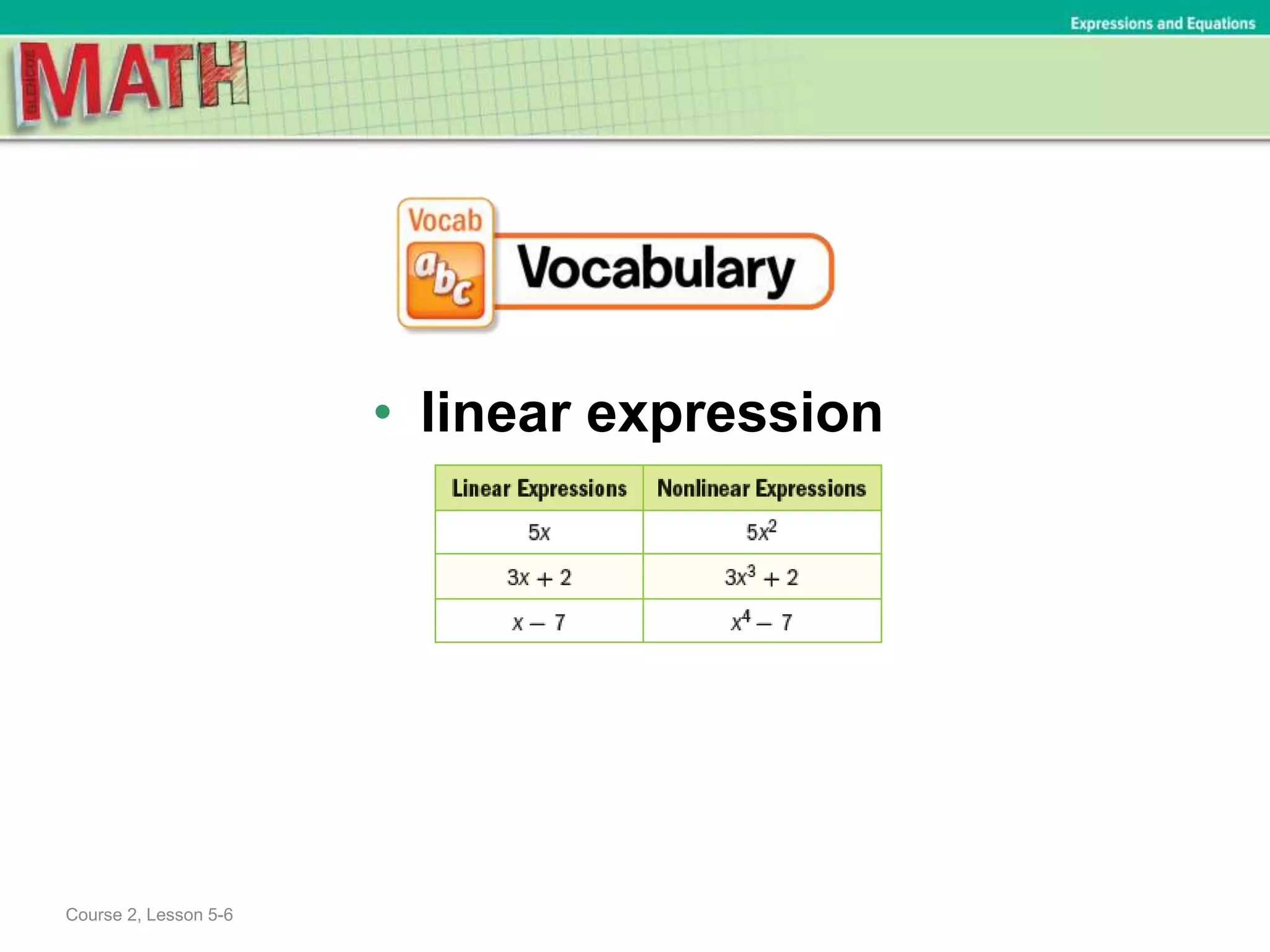
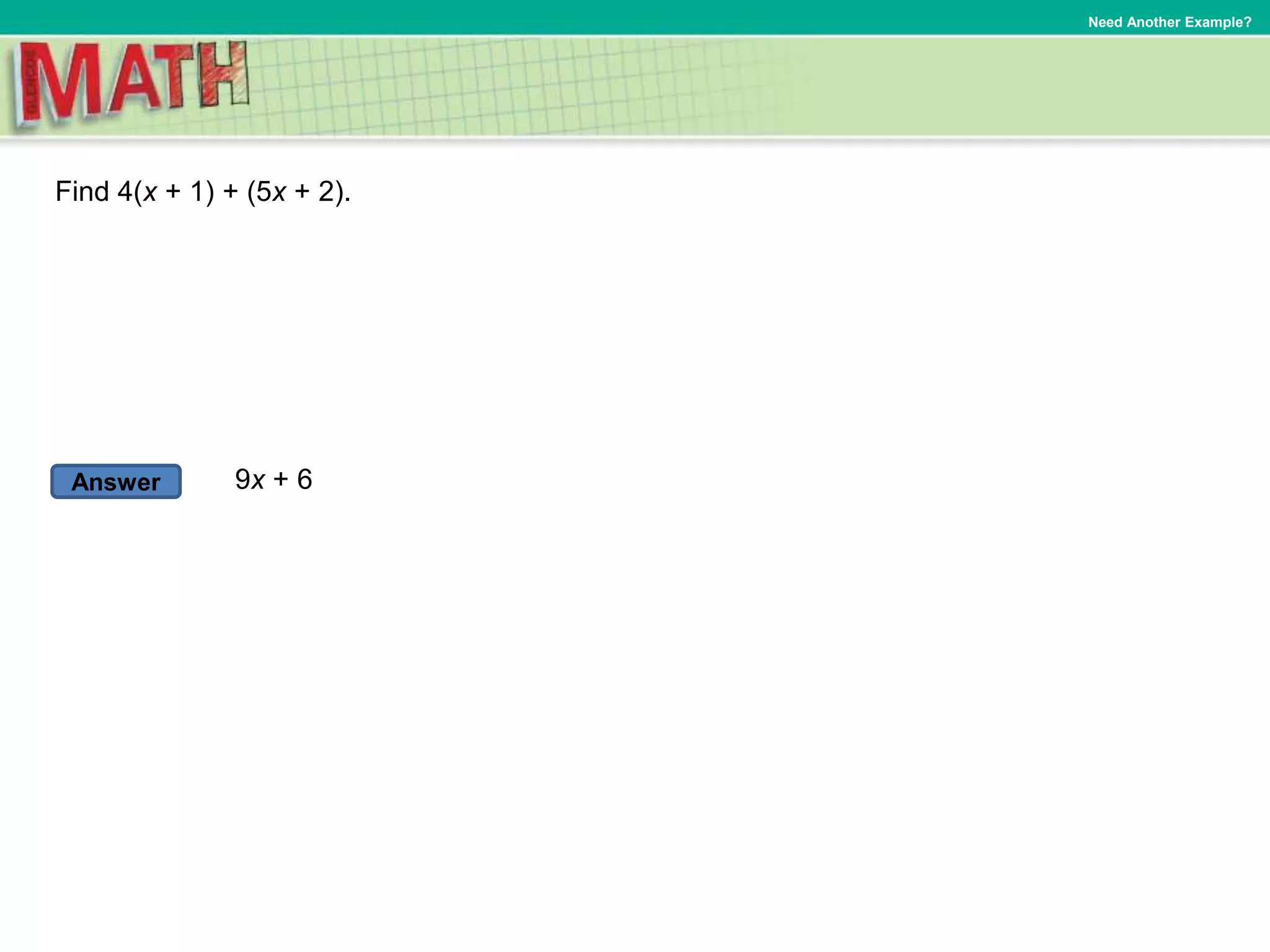
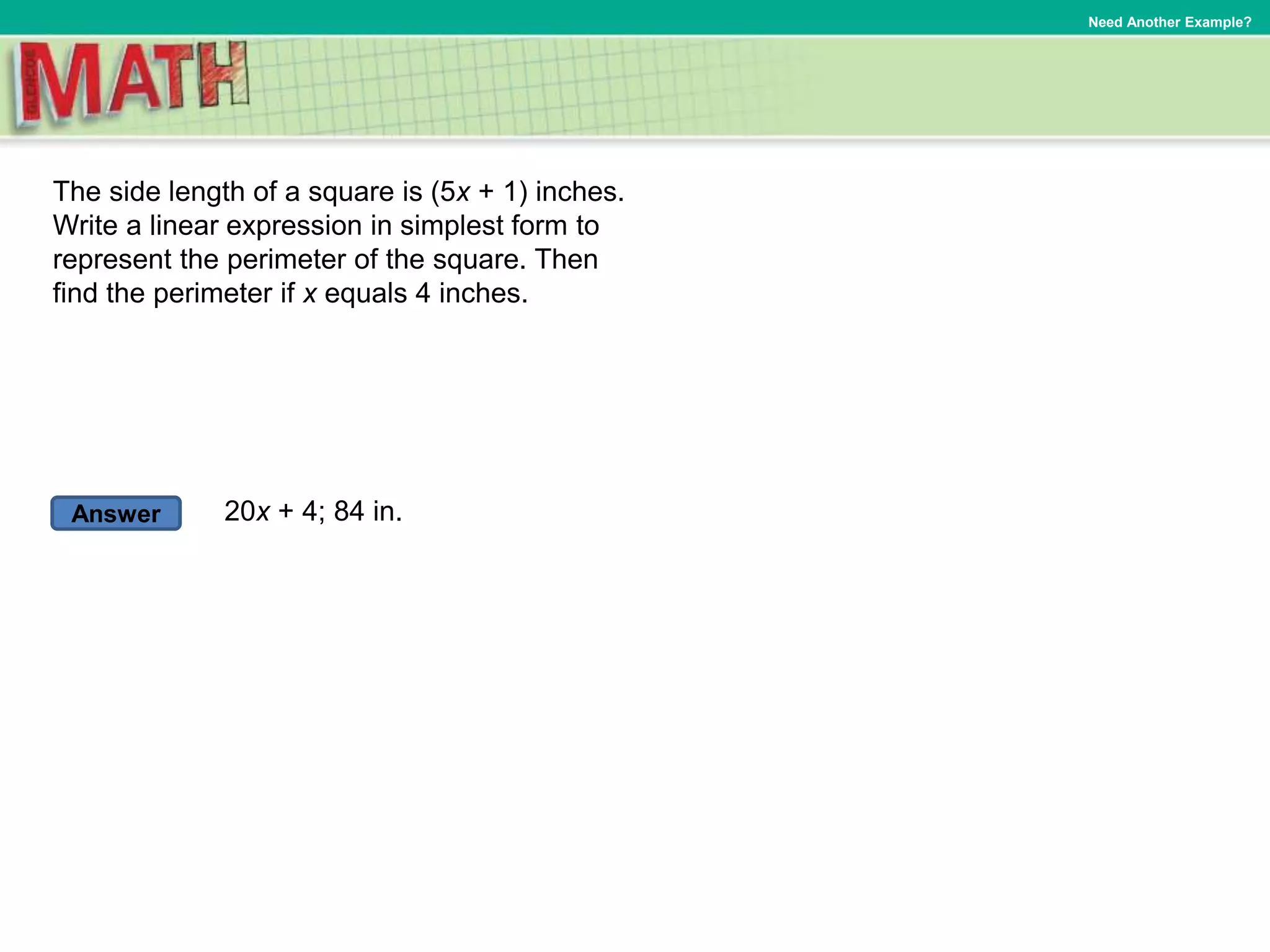
To add two linear expressions: 1. Arrange the terms of each expression in columns with like terms aligned. 2. Combine like terms by adding their coefficients. 3. Simplify the resulting expression by removing zero pairs and writing the expression in simplest form.

1. Identify the terms, like terms, coefficients, and constants in each
expression.
1. 8y – 3 + y 2. –22m – 2n + 1
Write each expression in simplest form.
3. 7k + 9k 4. 14h – 3 – 11h
5. Sara has x number of apples, 3 times as many oranges as apples,
and 2 peaches. Write an expression in simplest form that
represents the total number of pieces of fruit.
6. Write an expression to represent
the perimeter of the triangle.
Course 2, Lesson 5-6

2. Answers
1. terms: 8y, –3, y; like terms: 8y, y; coefficients: 8, 1;
constants: –3
2. terms: -22m, -2n, 1; no like terms; coefficients: -22, -2;
constants: 1
3. 16k
4. 3h – 3
5. 4x + 2
6. 5x + 1
Course 2, Lesson 5-6

3. HOW can you use numbers and
symbols to represent mathematical
ideas?
Expressions and Equations
Course 2, Lesson 5-6

4. • 7.EE.1
Apply properties of operations as strategies to add, subtract, factor,
and expand linear expressions with rational coefficients.
• 7.EE.2
Understand that rewriting an expression in different forms in a
problem context can shed light on the problem and how the quantities
in it are related.
Course 2, Lesson 5-6 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and
Council of Chief State School Officers. All rights reserved.
Expressions and Equations

5. Mathematical Practices
1 Make sense of problems and persevere in solving them.
2 Reason abstractly and quantitatively.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.
Course 2, Lesson 5-6 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and
Council of Chief State School Officers. All rights reserved.
Expressions and Equations

6. • To add linear expressions
Course 2, Lesson 5-6
Expressions and Equations

7. Course 2, Lesson 5-6
Expressions and Equations
• linear expression

8. 1
Need Another Example?
2
3
Step-by-Step Example
1. (2x + 3) + (x + 4)
Model each linear expression.
2x + 3
So, (2x + 3) + (x + 4) = 3x + 7.
x + 4
2x x 3 4+++
Combine like tiles and write a linear
expression for the combined tiles.

9. Answer
Need Another Example?
Find (6x + 2) + (x − 3).
7x – 1

10. 1
Need Another Example?
2
Step-by-Step Example
2. (2x – 1) + (x – 5)
Arrange like terms in columns.2x – 1
+ x – 5
So, (2x – 1) + (x – 5) = 3x – 6.
3x – 6 Add.

11. Answer
Need Another Example?
Find (4x – 2) + (x – 4).
5x – 6

12. 1
Need Another Example?
2
Step-by-Step Example
3. Find (2x – 3) + (–x + 4). Use models if needed.
Model each linear expression.
2x
So, (2x – 3) + (–x + 4) = x + 1.
x
Combine like tiles. Then remove all
zero pairs and write a linear
expression for the remaining tiles.
(–3) –x 4++
+ 1

13. Answer
Need Another Example?
Find (3x – 6) + (–2x + 7). Use models if needed.
x + 1

14. 1
Need Another Example?
2
3
4
Step-by-Step Example
4. Find 2(x + 3) + (3x + 1).
Use the Distributive Property.2(x + 3) + (3x +1)
So, 2(x + 3) + (3x + 1) = 5x + 7.
Arrange like terms
in columns.
= (2 • x + 2 • 3) + (3x + 1)
= (2x + 6) + (3x + 1) Simplify
2x + 6
+ 3x + 1
5x + 7 Add.

15. Answer
Need Another Example?
Find 4(x + 1) + (5x + 2).
9x + 6

16. 1
Need Another Example?
2
3
4
Step-by-Step Example
5. Find 5(x – 4) + (2x – 7).
Use the Distributive Property.5(x – 4) + (2x – 7)
So, 5(x – 4) + (2x – 7) = 7x – 27.
Arrange like terms
in columns.
= (5 • x – 5 • 4) + (2x – 7)
= (5x – 20) + (2x – 7) Simplify
5x – 20
+ 2x – 7
7x – 27 Add.

17. Answer
Need Another Example?
Find 3(x – 8) + (4x – 5).
7x – 29

18. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
6. Write a linear expression in simplest
form to represent the perimeter of the
triangle. Find the perimeter if the
value of x is 5 centimeters.
Write a linear expression for the perimeter of the triangle.
So, the perimeter of the triangle is 56 centimeters.
Replace x with 5. Simplify.
(3x – 3) + (2x + 9) + (5x) Write each expression.
Add.
(3x + 2x + 5x) + (–3 + 9) Rearrange to combine like terms.
10x + 6
Find the perimeter.
10x + 6 = 10(5) + 6 or 56

19. Answer
Need Another Example?
The side length of a square is (5x + 1) inches.
Write a linear expression in simplest form to
represent the perimeter of the square. Then
find the perimeter if x equals 4 inches.
20x + 4; 84 in.

20. How did what you learned
today help you answer the
HOW can you use numbers and symbols
to represent mathematical ideas?
Course 2, Lesson 5-6
Expressions and Equations

21. How did what you learned
today help you answer the
HOW can you use numbers and symbols
to represent mathematical ideas?
Course 2, Lesson 5-6
Expressions and Equations
Sample answers:
• By using algebra tiles to add linear expressions
• By combining like terms to add linear expressions
• By writing algebraic expressions in simplest form to
solve real-world problems

22. Write an explanation of
how to add two
linear expressions.
Ratios and Proportional RelationshipsExpressions and Equations
Course 2, Lesson 5-6