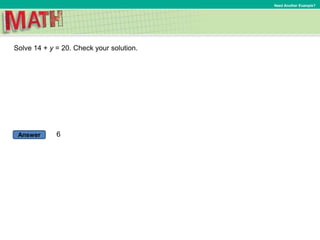
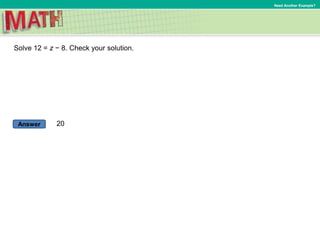
This document contains a mathematics lesson on solving equations using the subtraction and addition properties of equality. It includes examples of solving equations by applying these properties: subtracting or adding the same quantity to both sides of the equation to isolate the variable. The lesson defines key terms like equation, solution, and equivalent equations. It also includes examples of writing and solving equations to represent real-world problems involving quantities and their relationships.

1. Find the GCF of each pair of monomials.
1. 5x, 45
2. 18xy, 18
3. 72, 36g
4. 50ab, 200a
5. The perimeter of a square table is 12x + 4. What is
the length of one side of the table.
Course 2, Lesson 6-1

2. Answers
1. 5
2. 18
3. 36
4. 50a
5. 3x + 1
Course 2, Lesson 6-1

3. WHAT does it mean to say
two quantities are equal?
Expressions and Equations
Course 2, Lesson 6-1

4. • 7.EE.4
Use variables to represent quantities in a real-world or mathematical
problem, and construct simple equations and inequalities to solve
problems by reasoning about the quantities.
• 7.EE.4a
Solve real-world problems leading to equations of the form px + q = r
and p(x + q) = r, where p, q, and r are specific rational numbers. Solve
equations of these forms fluently. Compare an algebraic solution to an
arithmetic solution, identifying the sequence of operations used in each
approach.
Course 2, Lesson 6-1 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and
Council of Chief State School Officers. All rights reserved.
Expressions and Equations

5. Mathematical Practices
1 Make sense of problems and persevere in solving them.
2 Reason abstractly and quantitatively.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.
5 Use appropriate tools strategically.
Course 2, Lesson 6-1 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and
Council of Chief State School Officers. All rights reserved.
Expressions and Equations

6. How to solve equations using:
• The Subtraction Property of Equality
• The Addition Property of Equality
Course 2, Lesson 6-1
Expressions and Equations

7. Course 2, Lesson 6-1
Expressions and Equations
• equation
• solution
• equivalent equations
• Subtraction Property of Equality
• Addition Property of Equality

8. Course 2, Lesson 6-1
Expressions and Equations
Words The states that the two
sides of an equation remain equal when you subtract the
same number form each side.
Symbols If a = b, then a – c = b – c
Subtraction Property of Equality

9. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
1. Solve x + 6 = 4. Check your solution.
x + 6 = 4 Write the equation.
– 6 = –6 Subtraction Property of Equality
x = –2 Simplify.
Check x + 6 = 4
–2 + 6 = 4
4 = 4
Write the original equation.
Replace x with –2.
The sentence is true.
?
So, the solution is –2.

10. Answer
Need Another Example?
Solve 14 + y = 20. Check your solution.
6

11. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
2. Solve –5 = b + 8. Check your solution.
–5 = b + 8 Write the equation.
Subtraction Property of Equality
–13 = b Simplify.
Check –5 = b + 8
–5 = –13 + 8
–5 = –5
Write the original equation.
Replace x with –2.
The sentence is true.
?
So, the solution is –13.
–8 = –8

12. Answer
Need Another Example?
Solve –12 = 4 + c. Check your solution.
–16

13. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
3. An angelfish can grow to be 12 inches long. If an
angelfish is 8.5 inches longer than a clown fish,
how long is a clown fish?
12 = c + 8.5 Write the equation.
Subtraction Property of Equality
3.5 = c Simplify.
A clown fish is 3.5 inches long.
–8.5 = –8.5
Words
Variable
Equation
An angelfish is 8.5 inches longer than a clown fish.
Let c represent the length of the clown fish.
12 = c + 8.5

14. Answer
Need Another Example?
A grapefruit weighs 11 ounces, which is 6 ounces
more than an apple. Write and solve an equation
to find the weight of the apple.
a + 6 = 11; 5 ounces

15. Course 2, Lesson 6-1
Expressions and Equations
Addition Property of EqualityWords The states that the two
sides of an equation remain equal when you add the same
number to each side.
Symbols If a = b, then a + c = b + c.

16. 1
Need Another Example?
2
3
4
Step-by-Step Example
4. Solve x – 2 = 1. Check your solution.
x – 2 = 1 Write the equation.
Addition Property of Equality
x = 3 Simplify.
The solution is 3.
+ 2 = + 2
Check 3 – 2 = 1

17. Answer
Need Another Example?
Solve 12 = z − 8. Check your solution.
20

18. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
5. A pair of shoes costs $25. This is $14 less than the
cost of a pair of jeans. Find the cost of the jeans.
Shoes are $14 less than jeans. Let j represent the cost
of jeans.
Write the equation.
Addition Property of Equality
39 = j Simplify.
The jeans cost $39.
+ 14 = + 14
25 = j – 14

19. Answer
Need Another Example?
Vivian practiced the piano for 32 minutes. She
practiced 11 minutes less than her brother did.
Write and solve an equation to determine how
long her brother practiced the piano.
b − 11 = 32; 43 minutes

20. How did what you learned
today help you answer the
WHAT does it mean to say
two quantities are equal?
Course 2 Lesson 6-1
Expressions and Equations

21. How did what you learned
today help you answer the
WHAT does it mean to say
two quantities are equal?
Course 2 Lesson 6-1
Expressions and Equations
Sample answers:
• To solve equations using the Subtraction Property of
Equality
• To solve equations using the Addition Property of
Equality

22. Write the steps
you would use
to solve x – 3 = 19.
Course 2 Lesson 6-1
Ratios and Proportional RelationshipsExpressions and Equations