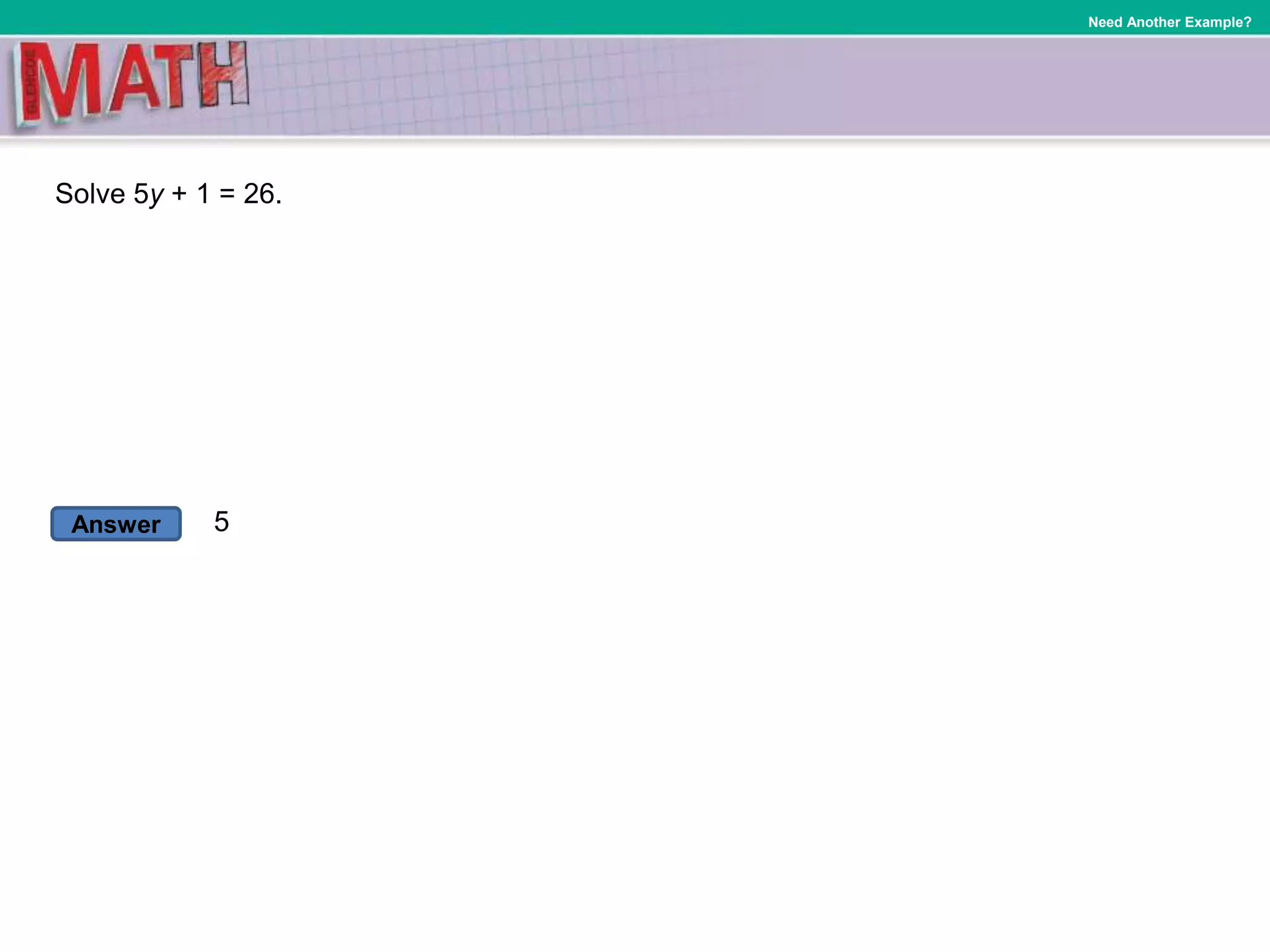
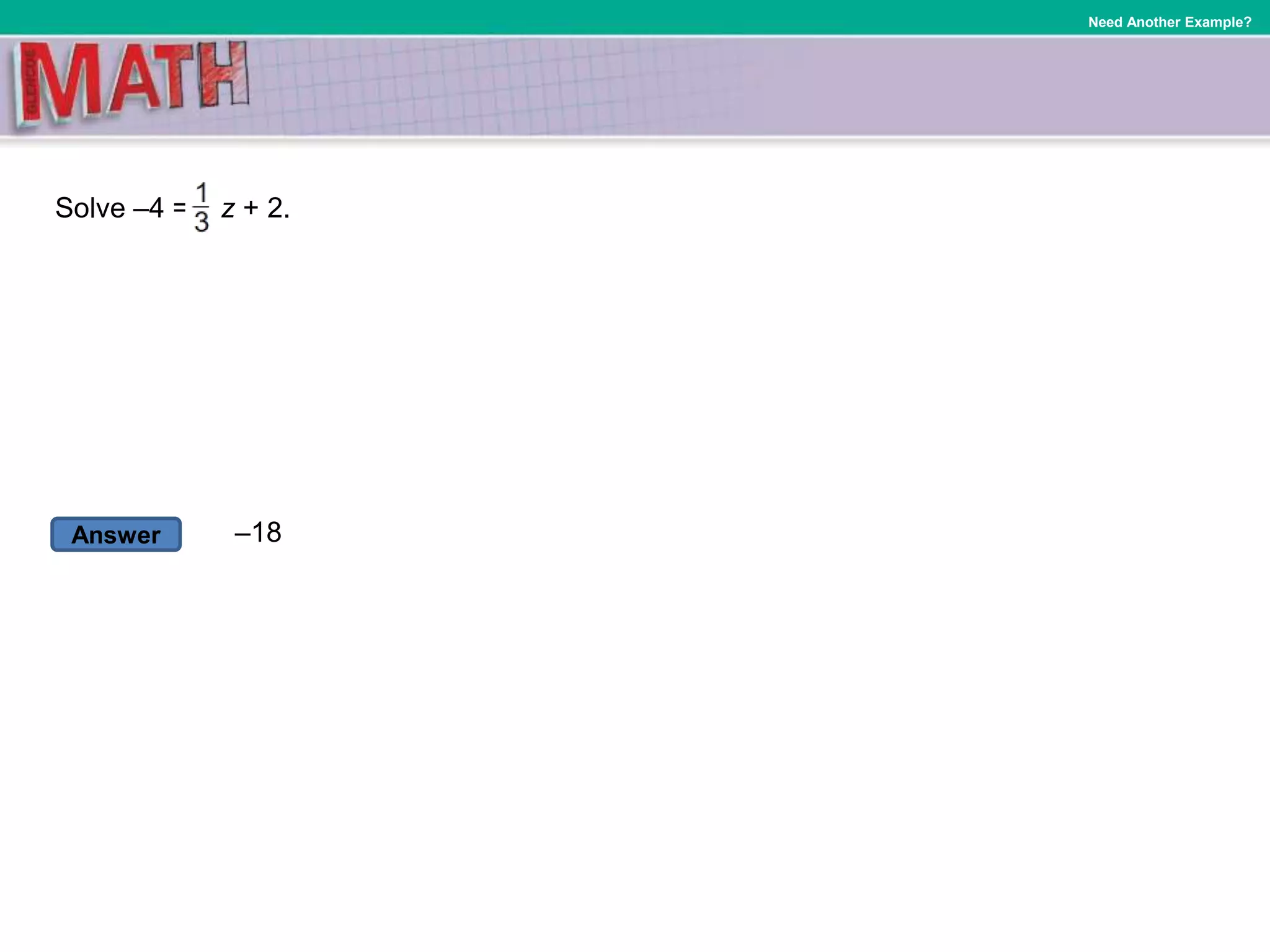
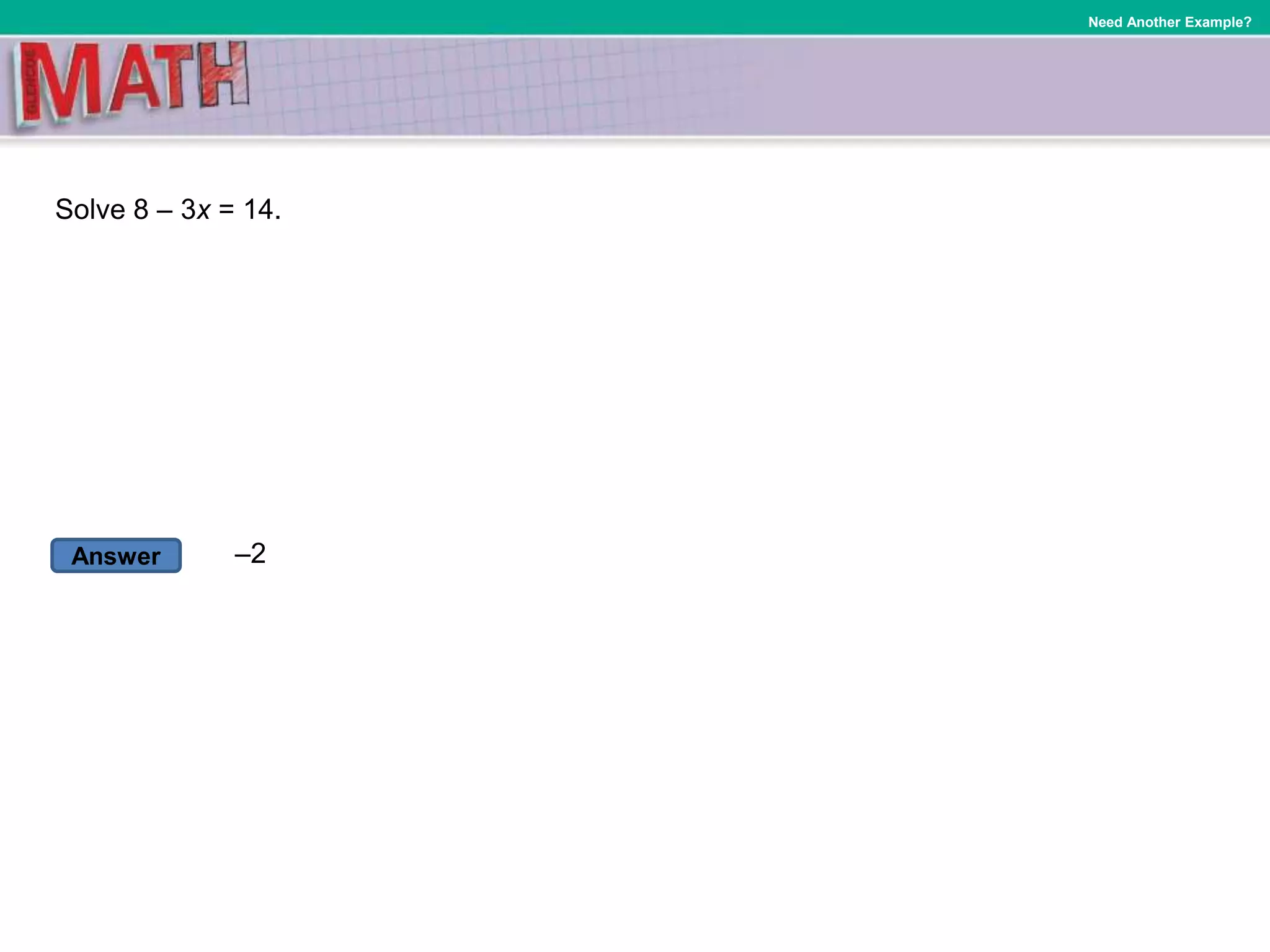
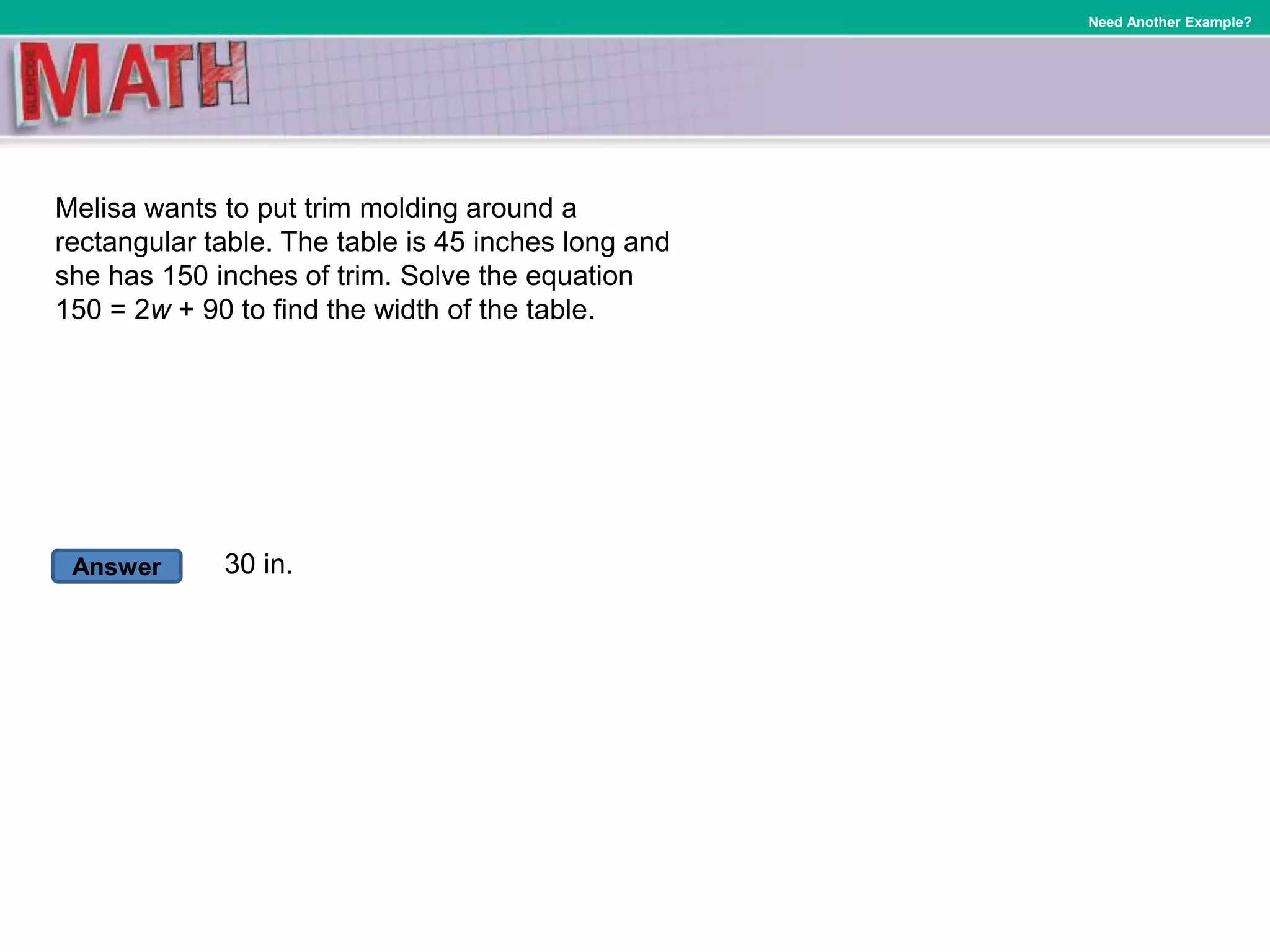
Here is a two-step equation example with steps to solve it: 2x + 3 = 11 Subtract 3 from both sides using the subtraction property of equality: 2x + 3 - 3 = 11 - 3 2x = 8 Divide both sides by 2 using the division property of equality: 2x/2 = 8/2 x = 4 To solve a two-step equation: 1) Use addition or subtraction to isolate the variable term on one side of the equation. 2) Use multiplication or division to solve for the variable. By applying the properties of equality, this allows you to transform the original equation into an equivalent equation where the variable term is alone

1. Course 3, Lesson 2-2
Solve each equation. Check your solution.
1. = 6
2. 0.6y = −12
3. =
4. 8.6n = −365.5
5. For art class, each student is going to make a piñata using
pound of paste. The art teacher bought 20 pounds of
paste. Write and solve an equation that can be used to
determine the number of students that can make a piñata.
4
5
3
4
n
1
2
2
x
1
22
2

2. Course 3, Lesson 2-2
Answers
1. 8
2. −20
3. 9
4. −42.5
5. ; n = 25
4
20
5
n 

3. WHAT is equivalence?
Expressions and Equations
Course 3, Lesson 2-2

4. • 8.EE.7
Solve linear equations in one variable.
• 8.EE.7a
Give examples of linear equations in one variable with one solution, infinitely
many solutions, or no solutions. Show which of these possibilities is the case
by successively transforming the given equation into simpler forms, until an
equivalent equation of the form x = a, a = a, or a = b results (where a and b
are different numbers).
• 8.EE.7b
Solve linear equations with rational number coefficients, including equations
whose solutions require expanding expressions using the distributive
property and collecting like terms.
Course 3, Lesson 2-2 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and Council of
Chief State School Officers. All rights reserved.
Expressions and Equations

5. Mathematical Practices
1 Make sense of problems and persevere in solving them.
2 Reason abstractly and quantitatively.
3 Construct viable arguments and critique the reasoning of others.
4 Model with mathematics.
Course 3, Lesson 2-2 Common Core State Standards © Copyright 2010. National Governors Association Center for Best Practices and Council of
Chief State School Officers. All rights reserved.
Expressions and Equations

6. To
• identify the Properties of Equality
• solve two-step equations
Course 3, Lesson 2-2
Expressions and Equations

7. • properties
• two-step equation
Course 3, Lesson 2-2
Expressions and Equations

8. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
1. Solve 2x + 3 = 7.
There are two 1-tiles in each group, so x = 2.
Write the equation.
Subtraction Property of Equality
Division Property of Equality
Remove three 1-tiles from each mat.
Separate the remaining tiles into 2 equal groups.
Using either method, the solution is 2.
7
Use a model.
2x + 3 – 3 = 7 – 3
2x = 4
Use symbols.
2x + 3 = 7
Simplify.x = 2.
–3 = –3
2x = 4

9. Answer
Need Another Example?
Solve 5y + 1 = 26.
5

10. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
2. Solve 25 = n – 3.
Write the equation.
Addition Property of Equality
Multiplication Property of Equality
25 = n – 3
28 = n
The solution is 112.
112 = n
Simplify.
+3 = +3

11. Answer
Need Another Example?
–18
Solve –4 = z + 2.

12. 1
Need Another Example?
2
3
4
5
6
Step-by-Step Example
3. Solve 6 – 3x = 21.
Write the equation.
Subtraction Property of Equality
Simplify.
–3x = 15
The solution is –5.
Simplify.
Rewrite the left side as addition.
6 – 3x = 21
6 + (–3x) = 21
x = –5
Division Property of Equality
Check 6 – 3x = 21 Write the equation.
Replace x with –5.
7
6 – 3(–5) = 21
?
6 – (–15) = 21
?
Multiply.
6 +15 = 21
?
To subtract a negative number, add its opposite.
21 = 21 The sentence is true.
–6 = –6

13. Answer
Need Another Example?
Solve 8 – 3x = 14.
–2

14. 1
Need Another Example?
2
3
4
5
Step-by-Step Example
4. Chicago’s lowest recorded temperature in degrees
Fahrenheit is –27°. Solve the equation –27 = 1.8C + 32 to
convert to degrees Celsius.
Write the equation.
Division Property of Equality
–32.8 ≈ C
Simplify.
Subtraction Property of Equality
–27 = 1.8C + 32
Simplify. Check the solution.
So, Chicago’s lowest recorded temperature is about
–32.8 degrees Celsius.
–32 = –32
–59 = 1.8C

15. Answer
Need Another Example?
Melisa wants to put trim molding around a
rectangular table. The table is 45 inches long and
she has 150 inches of trim. Solve the equation
150 = 2w + 90 to find the width of the table.
30 in.

16. How did what you learned
today help you answer the
WHAT is equivalence?
Course 3, Lesson 2-2
Expressions and Equations

17. How did what you learned
today help you answer the
WHAT is equivalence?
Course 3, Lesson 2-2
Expressions and Equations
Sample answers:
• In order to maintain the equality, when you perform an
operation on one side of an equation, you must
perform the same operation on the other side of the
equation.
• Equations are equivalent when they have the same
solution.

18. Write a two-step equation
and explain how to solve it.
Ratios and Proportional RelationshipsExpressions and Equations
Course 3, Lesson 2-2