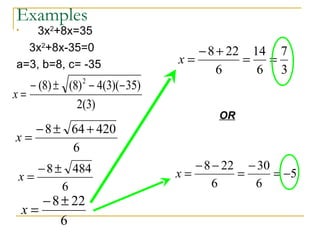
The document discusses the quadratic formula and discriminant. It states that the quadratic formula (ax^2 + bx + c = 0) should be used to solve a quadratic equation when it cannot be factored or when factoring is difficult. The discriminant (b^2 - 4ac) determines the number and type of solutions: a positive discriminant means there are 2 real solutions; a negative discriminant means there are 2 imaginary solutions; and a zero discriminant means there is 1 real solution. Examples are provided to demonstrate calculating the discriminant and classifying the solutions.

1. 5.6 Quadratic Formula & Discriminant

2. Quadratic Formula (Yes, it’s the one with the song!) If you take a quadratic equation in standard form (ax 2 +bx+c=0), and you complete the square, you will get the quadratic formula !

3. When to use the Quadratic Formula Use the quadratic formula when you can’t factor to solve a quadratic equation. (or when you’re stuck on how to factor the equation.)

4. Discriminant: b 2 -4ac The discriminant tells you how many solutions and what type you will have. If the discrim: Is positive : 2 real solutions Is negative : 2 imaginary solutions Is zero : 1 real solution

5. Examples Find the discriminant and give the number and type of solutions. 9x 2 +6x+1=0 a=9, b=6, c=1 b 2 -4ac=(6) 2 -4(9)(1) =36-36=0 1 real solution 9x 2 +6x-4=0 a=9, b=6, c=-4 b 2 -4ac=(6) 2 -4(9)(-4) =36+144=180 2 real solutions c. 9x 2 +6x+5=0 a=9, b=6, c=5 b 2 -4ac=(6) 2 -4(9)(5) =36-180=-144 2 imaginary solutions

6. Examples 3x 2 +8x=35 3x 2 +8x-35=0 a=3, b=8, c= -35 OR

7. -2x 2 =-2x+3 -2x 2 +2x-3=0 a=-2, b=2, c= -3