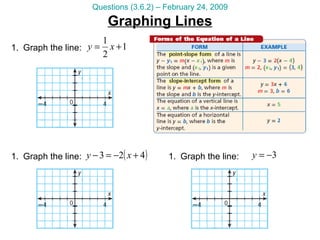
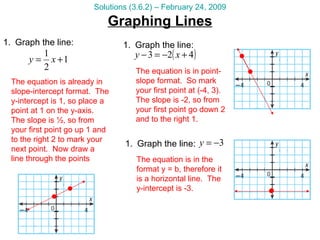
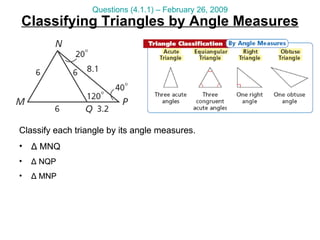
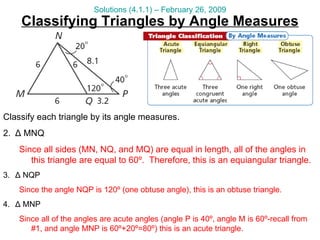
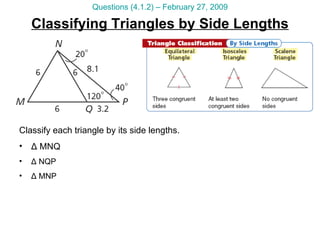
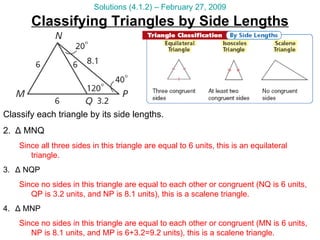
This document provides math tutorial questions and solutions for classifying triangles and writing equations of lines for the week of February 23-27. The questions cover writing equations of lines in point-slope and slope-intercept form, graphing lines, applying lines to word problems, and classifying triangles by angle and side length. The corresponding solutions provide step-by-step work and explanations for each question.

1. Math Tutorial Questions For the week of February 23 – February 27

2. Writing Equations of Lines Questions (3.6.1) – February 23, 2009 Write the equation of the line with slope 6 passing through (3, -4) in point-slope form. Write the equation of the line passing through (-1, 0) and (1, 2) in slope-intercept form. Write the equation of the line with x-intercept 3 and y-intercept -5 in point-slope form.

3. Writing Equations of Lines Solutions (3.6.1) – February 23, 2009 Write the equation of the line with slope 6 passing through (3, -4) in point-slope form. Point-slope form is y - y 1 = m(x - x 1 ) The slope is m = 6 The point is (x 1 , y 1 ) = (3, -4) So the point-slope form of the equation is y – (-4) = 6(x – 3) Write the equation of the line with x-intercept 3 and y-intercept -5 in point-slope form. Write the equation of the line passing through (-1, 0) and (1, 2) in slope-intercept form. y - y 1 = m(x - x 1 ) y – 0 = 1(x – (-1)) (Substitue values in for x 1 , y 1 , and m) y = 1(x + 1) (Cancel out – 0, - (-) turns into +) y = 1x + 1 (Distribute the 1 through the x + 1) y = x + 1 (The 1 in front of the x is understood to be there) First, the slope needs to be solved for: (x 1 , y 1 ) = (-1, 0) (x 2 , y 2 ) = (1, 2) Since the x-intercept is 3, this ordered pair would be (3, 0) = (x 1 , y 1 ) Since the y-intercept is -5, this ordered pair would be (0, -5) = (x 2 , y 2 ) The slope can now be solved for: y - y 1 = m(x - x 1 ) y – 0 = 5/3(x – 3) (Substitue values in for x 1 , y 1 , and m) y = 5/3(x – 3) (Cancel out – 0) y = 5/3x – 5 (Distribute the 5/3 through the x – 1)

4. Graphing Lines Questions (3.6.2) – February 24, 2009 Graph the line: Graph the line: Graph the line:

5. Graphing Lines Solutions (3.6.2) – February 24, 2009 Graph the line: Graph the line: Graph the line: The equation is already in slope-intercept format. The y-intercept is 1, so place a point at 1 on the y-axis. The slope is ½, so from your first point go up 1 and to the right 2 to mark your next point. Now draw a line through the points The equation is in point-slope format. So mark your first point at (-4, 3). The slope is -2, so from your first point go down 2 and to the right 1. The equation is in the format y = b, therefore it is a horizontal line. The y-intercept is -3.

6. Application of Lines in the Coordinate Plane Questions (3.6.4) – February 25, 2009 Erica is trying to decide between two car rental plans. For how many miles will the plans cost the same and what will that cost be? $0.50/mi $0.35/mi Mileage Fee $85 $100 Initial Fee Plan B Plan A Step 1: Understand the problem. Write down the information you are given and what you need to find. Step 2: Write and equation for each plan using slope-intercept form (y = mx +b). Step 3: Solve for x and y by one of two methods. a) By graphing both equations in your graphing calculator and find where they intersect. b) By substitution method, first solving for x, then y.

7. Step 3: y = 0.35x + 100 and y = 0.50x + 85 0.35x + 100 = 0.50x + 85 (since both equations equal y, set both equations equal to each other) 100 = 0.15x + 85 (subtract 0.35x from both sides) 15 = 0.15x (subtract 85 from both sides) 100 = x (divide both sides by 0.15) y = 0.35(100) + 100 (plug 100 in for x to either equation) y = 135 Application of Lines in the Coordinate Plane Solutions (3.6.4) – February 25, 2009 Erica is trying to decide between two car rental plans. For how many miles will the plans cost the same and what will that cost be? Step 2: Equation for Plan A: y = 0.35x + 100 Equation for Plan B: y = 0.50x + 85 Step 1: Plan A has an initial fee of $100 and charges $0.35 per mile. The number of miles will be represented by the variable x. Plan B has an initial fee of $85 and charges $0.50 per mile. The number of miles will be represented by the variable x. Therefore, after 100 miles, both plans will cost $135.

8. Classifying Triangles by Angle Measures Questions (4.1.1) – February 26, 2009 Classify each triangle by its angle measures. Δ MNQ Δ NQP Δ MNP Classify each triangle by its angle measures. Δ MNQ Δ NQP Δ MNP

9. Classify each triangle by its angle measures. Δ MNQ Since all sides (MN, NQ, and MQ) are equal in length, all of the angles in this triangle are equal to 60º. Therefore, this is an equiangular triangle. Δ NQP Since the angle NQP is 120º (one obtuse angle), this is an obtuse triangle. Δ MNP Since all of the angles are acute angles (angle P is 40º, angle M is 60º-recall from #1, and angle MNP is 60º+20º=80º) this is an acute triangle. Classifying Triangles by Angle Measures Solutions (4.1.1) – February 26, 2009

10. Classifying Triangles by Side Lengths Questions (4.1.2) – February 27, 2009 Classify each triangle by its side lengths. Δ MNQ Δ NQP Δ MNP

11. Classifying Triangles by Side Lengths Solutions (4.1.2) – February 27, 2009 Classify each triangle by its side lengths. Δ MNQ Since all three sides in this triangle are equal to 6 units, this is an equilateral triangle. Δ NQP Since no sides in this triangle are equal to each other or congruent (NQ is 6 units, QP is 3.2 units, and NP is 8.1 units), this is a scalene triangle. Δ MNP Since no sides in this triangle are equal to each other or congruent (MN is 6 units, NP is 8.1 units, and MP is 6+3.2=9.2 units), this is a scalene triangle.