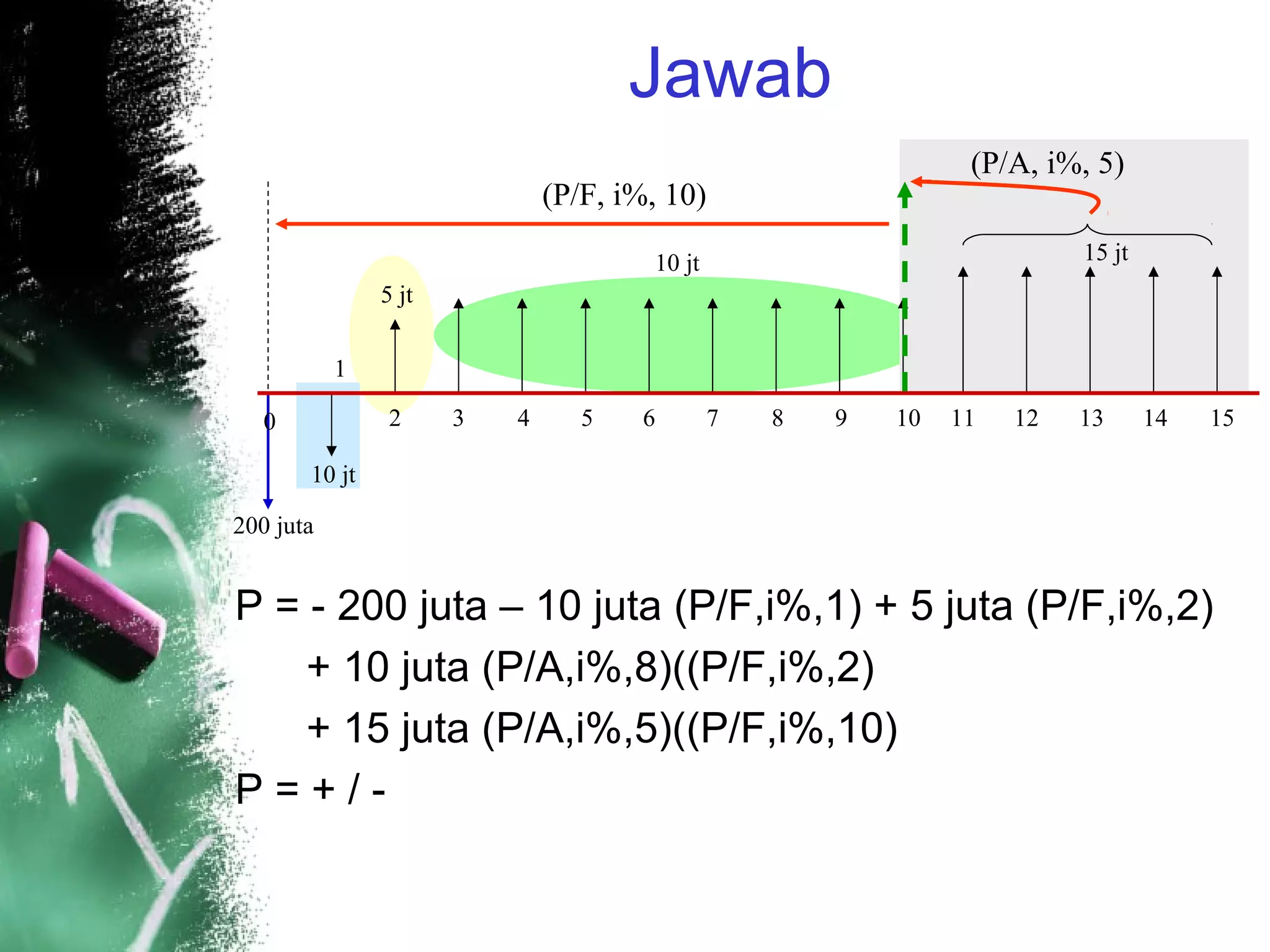
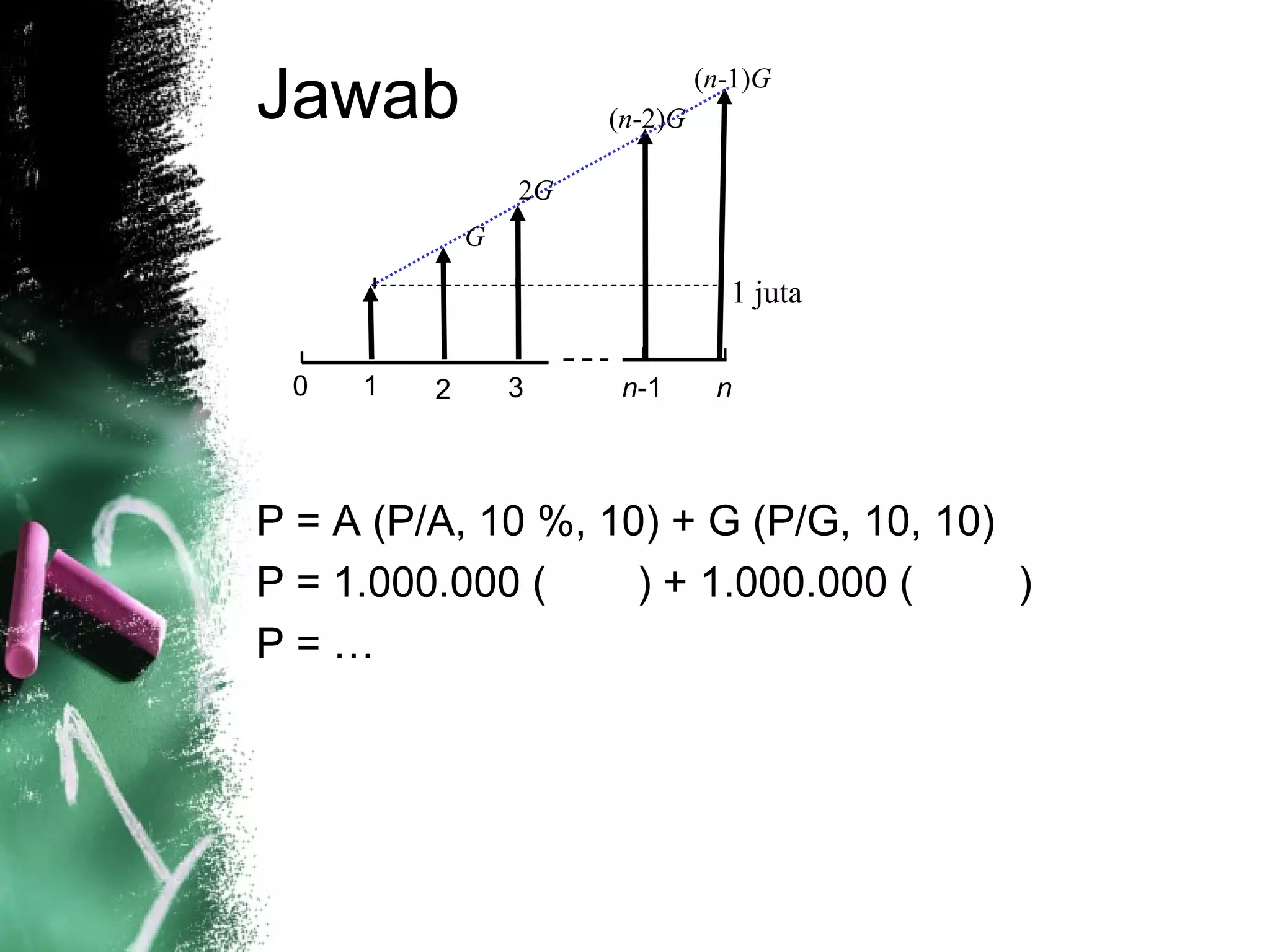
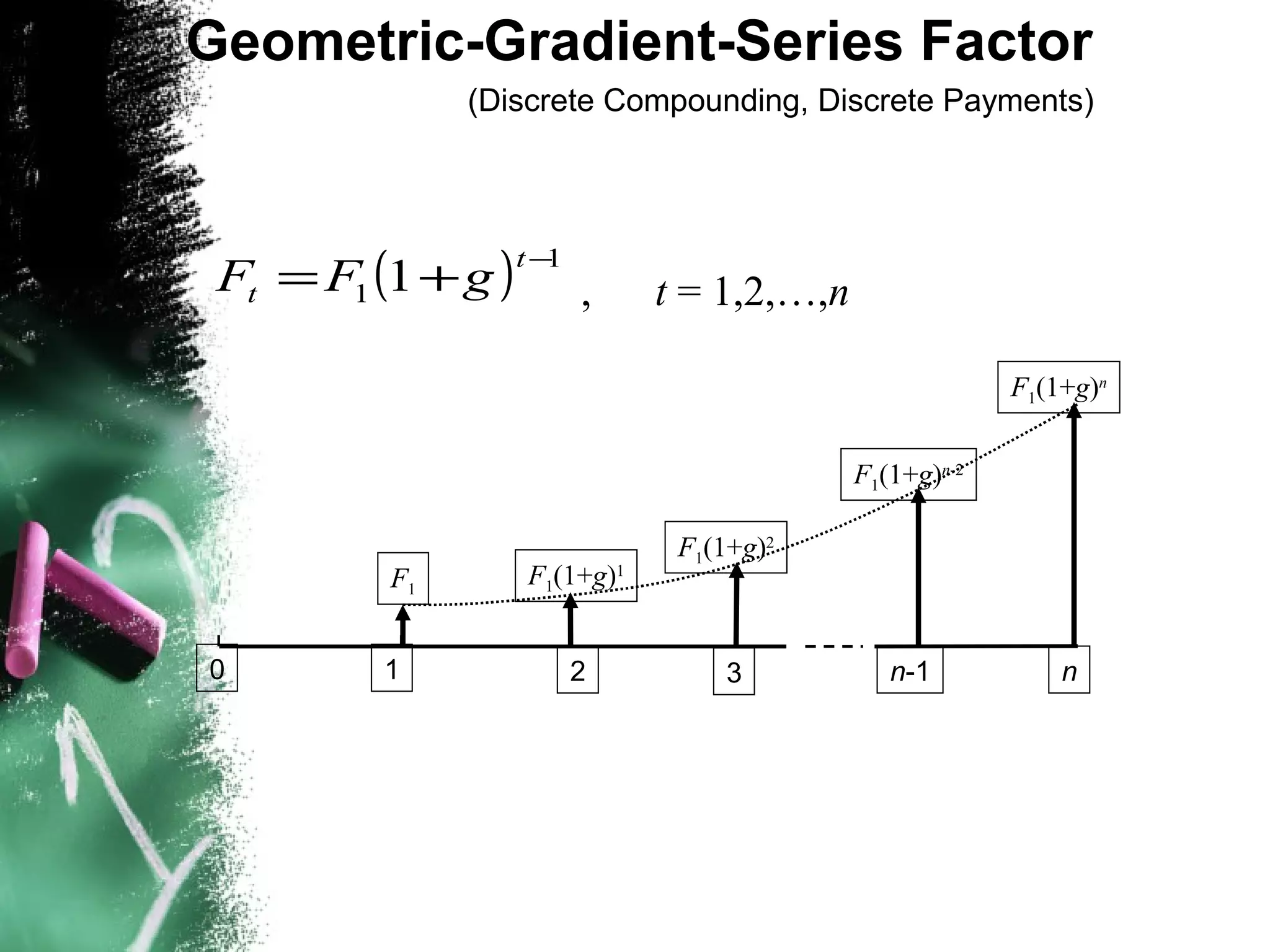
Dokumen ini menjelaskan konsep nilai uang berdasarkan waktu dengan berbagai contoh perhitungan cicilan, termasuk metode pembayaran kredit dan perbandingan investasi. Beberapa contoh praktis dihadirkan untuk menggambarkan penerapan rumus dalam situasi nyata, seperti pembelian mobil dan warisan. Selain itu, juga dibahas perhitungan arus kas tahunan untuk proyek investasi dengan mempertimbangkan modal kerja.