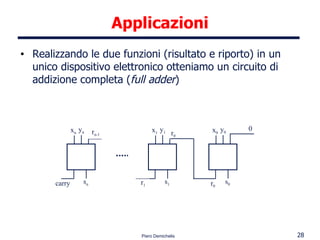
Il documento tratta dell'algebra booleana, sviluppata da George Boole nel XIX secolo, che si fonda sulla logica binaria con variabili che possono assumere solo i valori 0 e 1. Viene esplorata la definizione di funzioni booleane, la tavola della verità, gli operatori logici e le proprietà fondamentali che governano le operazioni su queste variabili. Infine, si menzionano le applicazioni dell'algebra booleana, inclusi circuiti elettrici e operazioni logiche, evidenziando la sua importanza in vari ambiti, dalla logica alla progettazione di dispositivi elettronici.

1. Algebra di Boole

2. La Logica Booleana Nel XIX secolo un matematico inglese, George Boole, si occupò della possibilità di ricondurre il ragionamento al rigore delle costruzioni matematiche, sviluppando l'algebra che ancor oggi porta il suo nome. Gli studi di Boole rimasero semplici esercizi teorici finché, all'inizio del ‘900, apparvero i primi dispositivi elettrici di commutazione (relays) e si rese necessario un supporto teorico per trattare questo tipo di circuiti.

3. La Logica Booleana Boole poneva alla base del ragionamento le asserzioni : queste possono essere solo vere o false , assumendo quindi due soli stati (0 e 1). Anche un circuito di commutazione può assumere solo due stati: chiuso (OFF) oppure aperto (ON). Da qui dunque l'analogia, e la possibilità di correlare situazioni apparentemente così differenti.

4. Variabili Booleane L'algebra booleana opera su variabili x 1 , x 2, …….., x n che possono assumere soltanto due valori: 0 e 1. Queste variabili prendono il nome di variabili logiche o booleane . Con esse si possono rappresentare eventi tipicamente binari: per esempio, un'affermazione può essere vera ( true = 1 ) oppure falsa ( false = 0) , un interruttore può essere aperto ( ON = 1) oppure chiuso ( OFF = 0) , ecc.

5. Funzioni Booleane Sulle variabili booleane può essere definita una funzione, detta funzione booleana , o funzione logica , F (x 1 , x 2, …….., x n ) , la quale, in corrispondenza di ogni n-pla x i , assume soltanto valori 0 e 1. Una particolare funzione booleana F è definita quando ad essa è assegnata la tavola della verità, tabella in cui è specificato il valore che assume F in corrispondenza di ogni combinazione delle variabili x 1 , x 2, …….., x n .

6. Tavola della Verità: esempio F V V V F V F V F F F F F( x 1 , x 2 ) x 2 x 1

7. Funzioni Booleane Il numero di combinazioni di n variabili è 2 n . Poiché per ogni combinazione delle n variabili una funzione può assumere 2 valori, 0 oppure 1, si possono avere 2 2 n funzioni diverse di n variabili. Ad esempio con 4 variabili si hanno 2 4 = 16 combinazioni e 2 16 = 65.536 possibili funzioni.

8. Esempio di Funzione Booleana In una stazione un treno parte se e solo se il semaforo è verde e il capotreno ha segnalato il via. Variabili logiche: T : vale 1 (vero) se il treno parte; S : vale 1 (vero) se il semaforo è verde; C : vale 1 (vero) se il capotreno ha dato il via . Tavola di verità: 1 1 1 0 0 1 0 1 0 0 0 0 T C S

9. Operatori Booleani Sulle variabili logiche agiscono gli operatori logici o booleani. Operatori fondamentali AND (  ) prodotto logico OR (  ) somma logica NOT (  ) negazione logica (complementazione) Gli operatori di somma e prodotto logico godono della proprietà associativa e distributiva come gli analoghi dell'algebra numerica.

10. Operatori Booleani Operatore AND Operatore OR Operatore NOT F V V F  A A V V V V F V V V F F F F A  B B A V V V F F V F V F F F F A  B B A

11. Precedenza degli Operatori Gerarchia degli operatori: NOT > AND > OR L’ordine può essere modificato tramite l’uso delle parentesi. Esempi: f = A  B  C  A  B f = A  B  ( C  A  B )

12. Espressioni Booleane Un insieme di variabili booleane, a cui siano applicati gli operatori logici AND, OR e NOT, prende il nome di espressione booleana o espressione logica T . Una espressione T corrisponde e può rappresentare quella funzione logica F che assume valore 1 in corrispondenza di quelle combinazioni di valori delle variabili per cui T = 1 e assume valore 0 in corrispondenza di quelle per cui T = 0 .

13. Notazione Per motivi pratici, la notazione viene così semplificata: AND • OR + NOT oppure ’ Esempio: A  (  B ) diventa: A + B oppure A + B’

14. Operatori Booleani non elementari NAND (NOT AND) NOR (NOT OR) • Falso se A e B sono veri Vero se A e B sono falsi F V V V F V V V F V F F A B B A F V V F F V F V F V F F A + B B A

15. Operatori Booleani non elementari EXOR (OR esclusivo) EXNOR (OR esclusivo negato) Vero se A diverso da B Vero se A uguale a B A A  B = A • B + A • B A  B = A • B + A • B F V V V F V V V F F F F A  B B A V V V F F V F V F V F F A  B B A

16. Espressione duale Una espressione T b è detta duale di una espressione T a se è ottenuta da quest'ultima sostituendo l'operatore AND con l'operatore OR, e viceversa, e la cifra 0 con la cifra 1, e viceversa. Esempio: T a = a • c + a • b + 0 T b = T ad = (a + c) • (a + b) • 1

17. Teoremi I teoremi dell’algebra logica possono essere utilizzati per dedurre espressioni che abbiano un minor numero di termini ( semplificazione delle espressioni logiche ). Al contrario dell'algebra ordinaria, dove non è possibile dimostrare i teoremi sostituendo alle variabili tutti i valori che possono assumere, nell'algebra booleana i teoremi sono dimostrabili per “induzione completa”, cioè verificandone la validità per tutte le combinazioni di valori (0 o 1) delle variabili. Per ogni teorema esiste il teorema duale , ottenuto applicando la regola di dualità. Si può dimostrare che, provata la validità di un teorema, risulta provata la validità anche del teorema duale.

18. Teoremi Proprietà commutativa A  B = B  A A + B = B + A Proprietà associativa A  B  C = (A  B)  C = A  (B  C) A + B + C = (A + B) + C = A + (B + C) Proprietà distributiva A  ( B + C ) = A  B + A  C A + ( B  C ) = ( A + B )  ( A + C )

19. Teoremi A  F = F A  V = A A + F = A A + V = V A  A = F A + A = V A = A A  A = A A  A = A A + A  B = A A  ( A + B ) = A A + A  B = A + B A  ( A + B ) = A  B

20. Teorema di De Morgan f ( a, b, ..., z; +,  ) = f ( a, b, ..., z;  , + ) Esempi: A + B = ( A  B ) ( A + B ) = A  B ( A  B ) = A  B

21. Espressione canonica Un problema logico viene espresso mediante frasi che esprimono le condizioni che devono essere soddisfatte affinché si verifichi qualche evento. Avendo enucleato le variabili booleane indipendenti, è possibile descrivere lo stesso problema per mezzo della tavola della verità della variabile indipendente (funzione booleana). Resta da fare un ultimo passo, ovvero il passaggio dalla tavola di verità all’espressione logica che la rappresenta.

22. Espressione canonica Per ottenere l’espressione logica dalla tavola di verità si può applicare la seguente regola pratica: l'espressione è formata da tanti termini, legati dall'operatore OR, quanti sono gli 1 della funzione; in ogni termine compaiono tutte le variabili indipendenti, legate dall'operatore AND, nella forma affermata o negata a seconda che per quella combinazione nella tavola della verità assumano il valore 1 o 0. L'espressione che si trova con questo metodo è detta canonica , ed è una delle tante espressioni equivalenti che possono rappresentare la stessa funzione.

23. Espressione canonica: esempio Esempio: si supponga che l’analisi del problema abbia condotto alla seguente tavola di verità: a b c d 1 1 1 1 0 0 1 1 1 1 0 1 0 0 0 1 1 1 1 0 0 0 1 0 1 1 0 0 0 0 0 0 F z y x

24. Espressione canonica: esempio Applicando alla precedente tavola di verità le regole per l’estrazione dell’ espressione canonica otteniamo la seguente espressione: F = x y z + x y z + x y z + x y z Questa espressione può essere ridotta con l’uso dei teoremi dell’algebra di Boole. a b c d

25. Minimizzazione dell’espressione F = x y z + x y z + x y z + x y z F = x z ( y + y ) + x z ( y + y ) F = x z + x z F = z ( x + x ) F = z =1 =1 =1

26. Applicazioni Il campo di applicazione dell’algebra di Boole è molto vasto, consentendo di risolvere problemi che, in origine, sono di natura molto diversa dalla logica. Ad esempio la somma di due numeri binari può essere ricondotta a una sequenza di somme elementari di 3 bit di ugual peso: 1 1 1 1 1 1 0 1 0 1 1 0 1 1 0 0 1 1 0 0 1 0 0 1 1 0 1 0 0 1 0 1 0 1 0 0 0 0 0 0 Rip S c y x

27. Applicazioni Considerando x, y e c variabili logiche possiamo scrivere: S = c • x • y + c • x • y + c • x • y + c • x • y = = c • ( x • y + x • y ) + c • ( x • y + x • y ) = = c • ( x  y ) + c • ( x  y ) = = c  x  y Un analoga funzione può essere scritta per il riporto risolvendo così, con semplicità, il problema della somma binaria

28. Applicazioni Realizzando le due funzioni (risultato e riporto) in un unico dispositivo elettronico otteniamo un circuito di addizione completa ( full adder ) x n y n r n-1 s n carry x 0 y 0 0 s 0 r 0 x 1 y 1 r 0 s 1 r 1