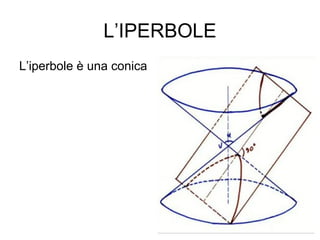
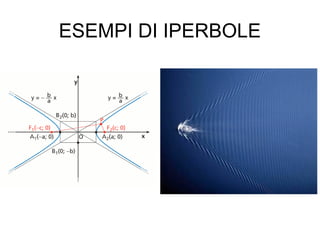
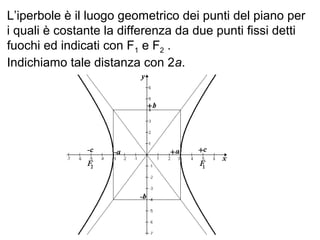
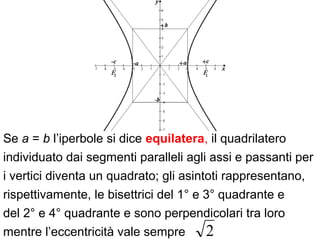
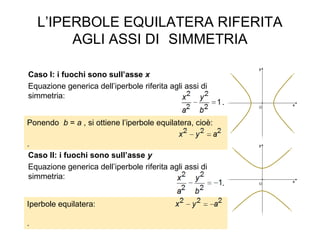
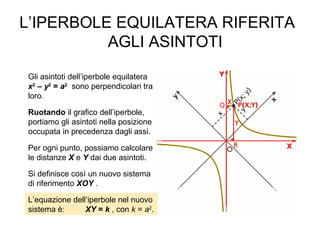
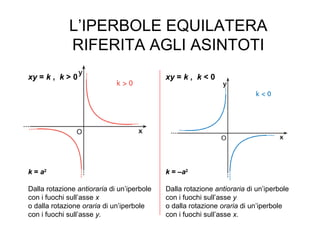
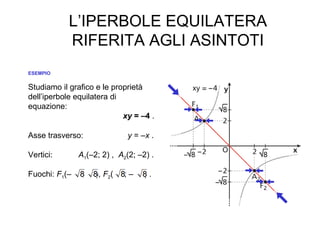
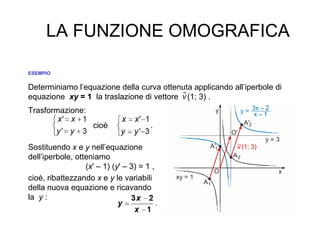
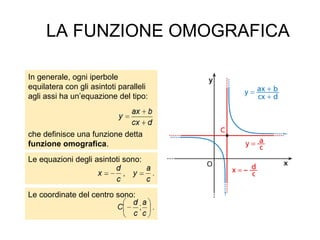
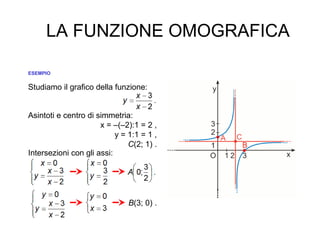
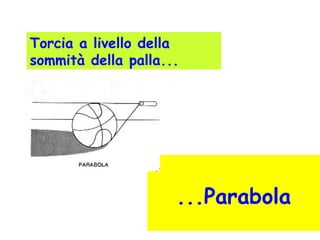
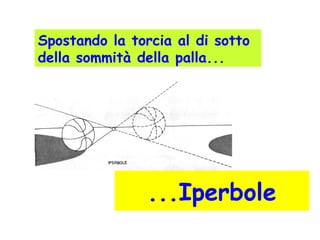
L'iperbole è una conica definita come il luogo geometrico dei punti nel piano per i quali la differenza delle distanze da due fuochi è costante. Il documento esplora le caratteristiche dell'iperbole, inclusa la sua equazione canonica, la simmetria rispetto agli assi, e il concetto di asintoti. Viene inoltre trattato il contributo di Apollonio nella comprensione delle coniche e delle loro proprietà.

1. APPROFONDIMENTO 4

2. L’IPERBOLE
L’iperbole è una conica

3. ESEMPI DI IPERBOLE

4. ESEMPI DI IPERBOLE

5. L’iperbole è il luogo geometrico dei punti del piano per
i quali è costante la differenza da due punti fissi detti
fuochi ed indicati con F1 e F2 .
Indichiamo tale distanza con 2a.

6. Quindi la relazione descrittiva è: aFPFP 221 =−
Poiché risulta che caFFFPFP 222121 <⇒<−
ovvero a < c.
Ricaviamo l’equazione dell’iperbole dalla definizione:
( ) ( ) ⇒±=+−−++ aycxycx 22222
( ) ( ) 2222
2 ycxaycx +−+±=++⇒

7. Elevando al quadrato entrambi i termini si ha:
( ) 222222222
4242 ycxayccxxayccxx +−⋅±++−+=+++
Riducendo i termini simili e dividendo per 4 si ha:
( ) cxaycxa −=+−⋅ 222
4
Elevando i nuovo al quadrato si ottiene:
( ) 22242222
22 xccxaayccxxa +−=++−⋅

8. Raccogliendo a fattore comune si può scrivere:
( ) ( )22222222
acayaxac −⋅=−⋅−
ac > 22
ac >
222
bac =−
Essendo e quindi, a maggior ragione
si può porre: e, quindi:
222222
bayaxb =−
22
bache, dividendo ambo i membri per
diventa:

9. 12
2
2
2
=−
b
y
a
x
che è l’equazione canonica o normale dell’iperbole
che ha i fuochi sull’asse x.
Se l’iperbole avesse i fuochi sull’asse y la sua
equazione canonica diverrebbe:
12
2
2
2
−=−
b
y
a
x

10. ( )0;a±
( )b±;0
L’iperbole gode delle seguenti proprietà e caratteristiche:
• la curva è simmetrica rispetto agli assi coordinati
• la curva interseca l’asse x in due punti detti vertici
reali di coordinate
e proietta sull’asse y due punti detti vertici non reali
di coordinate
• il segmento che congiunge i vertici reali viene detto
asse traverso mentre quello che congiunge i vertici
non reali viene detto asse non traverso
• l’iperbole è una curva aperta ed illimitata
• le rette passanti per l’origine e per i vertici opposti a
due a due del quadrilatero individuato dai segmenti
paralleli agli assi e passanti per i vertici vengono dette
asintoti

11. Il rapporto:
a
c
e =
è detto eccentricità ed è sempre maggiore di 1
Per ricavare l’equazione degli asintoti facciamo il
sistema tra l’equazione dell’iperbole e la retta generica
passante per l’origine:
xmy
b
y
a
x
⋅=
=− 12
2
2
2
222
mab
ab
x
−
±=⇒ e

12. 222
mab
mab
y
−
±=
222
mab −
a
b
mmab ±=⇒=− 0222
x
a
b
y += x
a
b
y −=
A seconda del valore della quantità
maggiore, uguale o minore a zero si ha che la retta è
secante, tangente o esterna all’iperbole, in quest’ultimo
caso, l’iperbole è tutta contenuta nello spazio
individuato dalle due rette (gli asintoti). Ponendo
e quindi le equazioni delle rette costituenti gli asintoti
sono:
e

13. Se a = b l’iperbole si dice equilatera, il quadrilatero
individuato dai segmenti paralleli agli assi e passanti per
i vertici diventa un quadrato; gli asintoti rappresentano,
rispettivamente, le bisettrici del 1° e 3° quadrante e
del 2° e 4° quadrante e sono perpendicolari tra loro
mentre l’eccentricità vale sempre 2

14. Poiché l’equazione dell’iperbole contiene due parametri
(a e b), per determinarla univocamente occorrono due
condizioni che possono essere:
1.passaggio per due punti (non simmetrici rispetto agli
assi o rispetto all’origine);
2.conoscenza delle coordinate di un fuoco e della
equazione di un asintoto;
3.conoscenza delle coordinate di un vertice e di un fuoco.
(si ricorda che )
222
bac =−
Se l’iperbole è equilatera è sufficiente una sola
condizione purché non sia la conoscenza degli asintoti
o l’eccentricità.

15. Caso I: i fuochi sono sull’asse x
Equazione generica dell’iperbole riferita agli assi di
simmetria:
Ponendo b = a , si ottiene l’iperbole equilatera, cioè:
.
Iperbole equilatera:
.
.
Caso II: i fuochi sono sull’asse y
Equazione generica dell’iperbole riferita agli assi di
simmetria:
.
L’IPERBOLE EQUILATERA RIFERITA
AGLI ASSI DI SIMMETRIA

16. L’IPERBOLE EQUILATERA RIFERITA
AGLI ASSI DI SIMMETRIA
Iperbole equilatera:
x2
– y2
= a2
, b = a .
Asintoti
Formula generale :
. Asintoti: y = x , y = –x .
Eccentricità
Formula generale
.
Eccentricità:
.
ESEMPIO
L’iperbole di equazione
x2
– y2
= 9
ha per vertici: A1(–3;0) , A2(3;0) ,
B1(–3;0) , B2(3;0) .
I fuochi sono: F1(–3 ;0) , F2(3 ;0) .
Gli asintoti sono: y = x , y = –x .

17. L’IPERBOLE EQUILATERA RIFERITA
AGLI ASINTOTI
Gli asintoti dell’iperbole equilatera
x2
– y2
= a2
sono perpendicolari tra
loro.
Ruotando il grafico dell’iperbole,
portiamo gli asintoti nella posizione
occupata in precedenza dagli assi.
Per ogni punto, possiamo calcolare
le distanze X e Y dai due asintoti.
Si definisce così un nuovo sistema
di riferimento XOY .
L’equazione dell’iperbole nel nuovo
sistema è: XY = k , con k = a2
.

18. L’IPERBOLE EQUILATERA
RIFERITA AGLI ASINTOTI
xy = k , k > 0
k = a2
Dalla rotazione antioraria di un’iperbole
con i fuochi sull’asse x
o dalla rotazione oraria di un’iperbole
con i fuochi sull’asse y.
xy = k , k < 0
k = –a2
Dalla rotazione antioraria di un’iperbole
con i fuochi sull’asse y
o dalla rotazione oraria di un’iperbole
con i fuochi sull’asse x.

19. L’IPERBOLE EQUILATERA
RIFERITA AGLI ASINTOTI
Vertici e fuochi
Vertici:
Fuochi:
k > 0
Vertici:
Fuochi:
k < 0

20. L’IPERBOLE EQUILATERA
RIFERITA AGLI ASINTOTI
ESEMPIO
Studiamo il grafico e le proprietà
dell’iperbole equilatera di
equazione:
xy = –4 .
Asse trasverso: y = –x .
Vertici: A1(–2; 2) , A2(2; –2) .
Fuochi: F1(– ; ), F2( ; – ) .

21. LA FUNZIONE OMOGRAFICA
ESEMPIO
Determiniamo l’equazione della curva ottenuta applicando all’iperbole di
equazione xy = 1 la traslazione di vettore (1; 3) .
Trasformazione:
cioè .
Sostituendo x e y nell’equazione
dell’iperbole, otteniamo
(x' – 1) (y' – 3) = 1 ,
cioè, ribattezzando x e y le variabili
della nuova equazione e ricavando
la y :

22. LA FUNZIONE OMOGRAFICA
In generale, ogni iperbole
equilatera con gli asintoti paralleli
agli assi ha un’equazione del tipo:
che definisce una funzione detta
funzione omografica.
Le equazioni degli asintoti sono:
Le coordinate del centro sono:

23. LA FUNZIONE OMOGRAFICA
ESEMPIO
Studiamo il grafico della funzione:
Asintoti e centro di simmetria:
x = –(–2):1 = 2 ,
y = 1:1 = 1 ,
C(2; 1) .
Intersezioni con gli assi:
B(3; 0) .

24. ESERCIZI: L’IPERBOLE EQUILATERA
RIFERITA AGLI ASSI DI SIMMETRIA

25. ESERCIZI: L’IPERBOLE EQUILATERA
RIFERITA AGLI ASSI DI SIMMETRIA

26. Matematici greciMatematici greci
Le curve non venivano definite come luoghi del
piano che soddisfano una certa condizione,
ma con il seguente ordine:
r e t t e
c e r c h i
l u o g h i p i a n i
s e z i o n i c o n i c h e
l u o g h i s o l i d i
t u t t e l e a l t r e c u r v e
l u o g h i l i n e a r i
t r e c a t e g o r i e

27. ApollonioApollonio (Biografia)(Biografia)
Apollonio Pergeo (Perga, Panfilia 262 a.C. ca. - ? 180
a.C.), matematico greco. Studiò le matematiche ad
Alessandria d'Egitto; scrisse di calcolo aritmetico ed
elaborò i fondamenti della disciplina antenata
dell'attuale geometria proiettiva con le Coniche, opera
che constava originariamente di otto libri, di cui solo i
primi quattro sono giunti fino a noi scritti in greco,
mentre i tre libri rimasti dei quattro seguenti sono noti
solo attraverso traduzioni arabe. Apollonio fornì inoltre
un grande contributo all'astronomia greca, applicando
modelli geometrici al movimento dei pianeti.

28. Pensiero di Apollonio
Affermò che da un unico cono era
possibile ottenere tutte e tre le
varietà di sezioni coniche,
semplicemente variando l’inclinazione
del piano d’intersezione.
Dimostrò che le proprietà delle curve
non cambiano, se intersecate in coni
obliqui o in coni retti.

29. ““Le conicheLe coniche”
Trattati di Apollonio
(1°libro) Tratta le proprietà fondamentali
delle curve in maniera più completa e
generale di quanto fosse stato fatto negli
scritti degli altri autori.
(2°libro) Continua lo studio dei diametri
coniugati e delle tangenti.
(3°libro) Contiene molti teoremi notevoli, utili
per la sintesi dei luoghi solidi e per la
determinazione dei limiti.
(4°libro) Apollonio illustra in quanti modi le
sezioni coniche possono incontrarsi l’una con
l’altra.

30. (5°libro) Tratta i segmenti massimi e minimi che
si possono tracciare rispetto a una conica.
(6°libro) Abbraccia proposizioni concernenti
segmenti di coniche uguali e disuguali, oltre ad
altre questioni trascurate da altri autori.
(7°libro) Ritorna sull’argomento dei diametri
coniugati e contiene molte nuove proposizioni
concernenti diametri di sezione e le figure
descritte su di esse.
(8°libro)Tratta problemi simili.
““Le conicheLe coniche”
Trattato di Apollonio

31. Costruzione delle coniche
Proviamo a costruire le coniche
usando un pallone da basket, una
torcia e un piano bianco sul quale
proiettare l’ombra del pallone.
Posizioniamo la torcia secondo
diverse angolazioni e osserviamo cosa
succede...

32. ...Parabola
Torcia a livello della
sommità della palla...

33. ...Circonferenza
Proiettando un fascio di luce
perpendicolare alla palla...

34. ...Ellisse
Spostando la torcia verso
destra...

35. ...Iperbole
Spostando la torcia al di sotto
della sommità della palla...