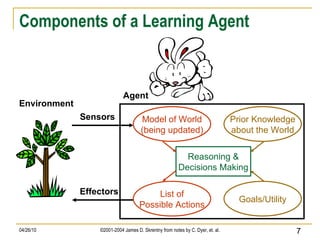
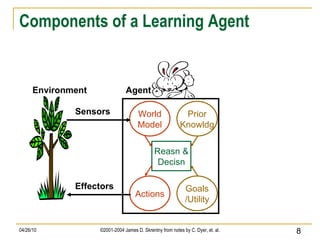
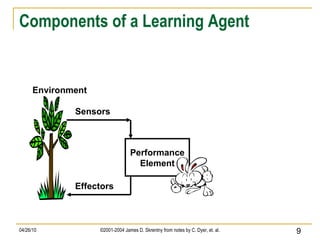
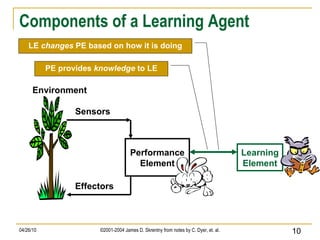
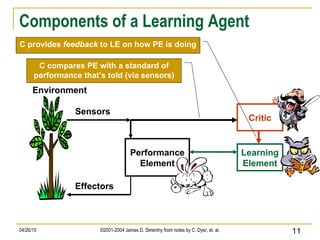
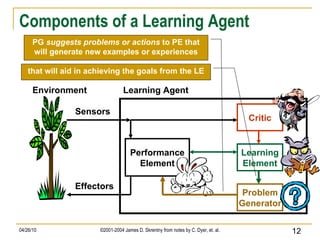
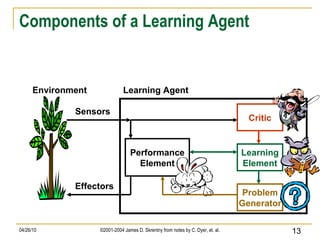
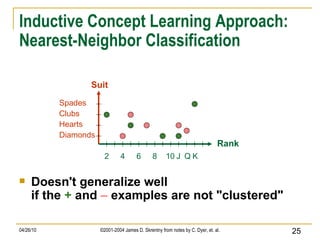
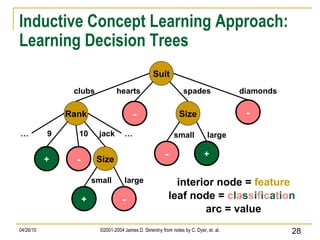
The document discusses concepts related to supervised machine learning and decision tree algorithms. It defines key terms like supervised vs unsupervised learning, concept learning, inductive bias, and information gain. It also describes the basic process for learning decision trees, including selecting the best attribute at each node using information gain to create a small tree that correctly classifies examples, and evaluating performance on test data. Extensions like handling real-valued, missing and noisy data, generating rules from trees, and pruning trees to avoid overfitting are also covered.

1. Learning From Observations Chapter 18.1-18.3 Quotes & Concept Components of the Learning Agent Supervised Concept Learning by Induction Inductive Bias Inductive Concept Learning Framework and Approaches Decision Tree Algorithm

2. Learning? "Learning is making useful changes in our minds." Marvin Minsky

3. Learning? "Learning is constructing or modifying representations of what is being experienced." Ryszard Michalski

4. Learning? "Learning denotes changes in a system that ... enable a system to do the same task more efficiently the next time." Herbert Simon 1916 - 2001

5. Learning? What are different paradigms of learning? Rote Learning Induction Clustering Analogy Discovery Genetic Algorithms Reinforcement

6. Learning? Why do machine learning? Understand and improve efficiency of human learning Discover new things or structures that are unknown to humans Fill in skeletal or incomplete specifications about a domain

7. Components of a Learning Agent Environment Agent Reasoning & Decisions Making Sensors Effectors Model of World (being updated) List of Possible Actions Prior Knowledge about the World Goals/Utility

8. Components of a Learning Agent Environment Sensors Effectors Agent Reasn & Decisn World Model Actions Prior Knowldg Goals /Utility

9. Components of a Learning Agent Environment Sensors Effectors Performance Element

10. Components of a Learning Agent Environment Performance Element Learning Element Sensors Effectors PE provides knowledge to LE LE changes PE based on how it is doing

11. Components of a Learning Agent Environment Performance Element Learning Element Sensors Effectors Critic C provides feedback to LE on how PE is doing C compares PE with a standard of performance that’s told (via sensors)

12. Components of a Learning Agent Environment Performance Element Learning Element Sensors Effectors Critic Problem Generator PG suggests problems or actions to PE that will generate new examples or experiences that will aid in achieving the goals from the LE Learning Agent

13. Components of a Learning Agent Environment Performance Element Critic Learning Element Problem Generator Sensors Effectors Learning Agent

14. Supervised Concept Learning by Induction What is inductive learning (IL)? Its learning from examples. IL extrapolates from a given set of examples so that accurate predictions can be made about future examples. Learn unknown function: f(x) = y x : an input example y : the desired output h (hypothesis) is learned which approximates f

15. Supervised Concept Learning by Induction Why is inductive learning an inherently conjectural process? any knowledge created by generalization from specific facts cannot be proven true it can only be proven false Inductive inference is falsity preserving, not truth preserving. An induction produces an hypothesis that must be validated by relating to new fact or experiments. It is only an opinion and not necessarily true.

16. Supervised Concept Learning by Induction What is supervised vs. unsupervised learning? supervised: "teacher" gives a set of both the input examples and desired outputs, i.e. (x, y) pairs unsupervised: only given the input examples, i.e. the x s In either case, the goal is to determine an hypothesis h that estimates f .

17. Supervised Concept Learning by Induction What is concept learning (CL)? CL determines from a given a set of examples if a given example is or isn't an instance of the concept/class/category. If it is, call it a positive example = + If not, called it a negative example = -

18. Supervised Concept Learning by Induction What is supervised CL by induction ? Given a training set of positive and negative examples of a concept: {(x 1 , y 1 ), (x 2 , y 2 ), ..., (x n , y n )} each x i is an example each y i is the classification, either + or - Construct a description that accurately classifies whether future examples are positive or negative: h(x n+1 ) = y n+1 where y n+1 is the prediction, either + or –

19. Supervised Concept Learning by Induction How might the performance of this learning algorithm be evaluated? predictive accuracy of classifier (most common) speed of learner speed of classifier space requirements

20. Inductive Bias Learning can be viewed as searching the Hypothesis Space H of possible h functions. Inductive Bias: is when one h is chosen over another is needed to generalize beyond the specific training examples Completely unbiased inductive algorithm only memorizes training examples (rote learning) can't predict about unseen examples

21. Inductive Bias Biases commonly used in machine learning Restricted Hypothesis Space Bias : allow only certain types of h s, not arbitrary ones Preference Bias : define a metric for comparing h s so as to determine whether one is better than another

22. Inductive Concept Learning Framework Preprocess raw sensor data extract a feature vector, x , that describes attributes relevant for classifying examples Each x is a list of (attribute, value) pairs x = (Rank,queen), (Suit,hearts), (Size,big) number of attributes is fixed: Rank Suit Size number of possible values for each attribute is fixed Rank : 2 ..10 jack queen king ace Suit : diamonds hearts clubs spades Size : big small

23. Inductive Concept Learning Framework Each example can be interpreted as a point in an n-dimensional feature space, where n is the number of attributes. Suit Rank spades clubs hearts diamonds 2 4 6 8 10 J Q K

24. Inductive Concept Learning Approach: Nearest-Neighbor Classification Nearest Neighbor , a simple approach: save each training example as a point in Feature Space classify a new example by giving it the same classification ( + or - ) as its nearest neighbor in Feature Space

25. Inductive Concept Learning Approach: Nearest-Neighbor Classification Doesn't generalize well if the + and – examples are not "clustered" Suit Rank Spades Clubs Hearts Diamonds 2 4 6 8 10 J Q K

26. Inductive Concept Learning Approach: Learning Decision Trees Goal: Build a decision tree for classifying examples as positive or negative instances of a concept is form of supervised concept learning by induction uses preference & restricted hypothesis space bias has two phases: learning : uses batch processing of training examples to produce a classifier classifying : uses classifier to make predictions about unseen examples

27. Inductive Concept Learning Approach: Learning Decision Trees A decision tree is a tree in which: each non-leaf node has associated with it an attribute (feature) each leaf node has associated with it a classification (+ or -) each arc has associated with it one of the possible values of its parent node’s attribute

28. Inductive Concept Learning Approach: Learning Decision Trees Suit Rank - clubs hearts spades - + Size - + large small 9 jack 10 Size + - large small interior node = feature leaf node = c l a s s i f i c a t i o n arc = value - diamonds … …

29. Inductive Concept Learning Approach: Learning Decision Trees Preference Bias: Ockham's Razor The simplest hypothesis that is consistent with all observations is most likely. The smallest decision tree that correctly classifies all of the training examples is best. Finding the provably smallest decision tree is an NP-Hard problem, so instead construct one that is pretty small.

30. Learning From Observations Chapter 18.1-18.3 Decision Tree Algorithm Information Gain Selecting the Best Attribute Case Studies & Extensions Pruning

31. Decision Tree Algorithm ID3 or C5.0, first developed by Quinlan (1987) Top-down construction of the decision tree using a greedy algorithm: Select the "best attribute" to use for the new node at the current level in the tree. For each possible value of the selected attribute: Partition the examples using the possible values of this attribute, and assign these subsets of the examples to the appropriate child node. Recursively generate each child node until (ideally) all examples for a node are either all + or all -.

32. Decision Tree Algorithm Node decisionTreeLearning ( exs, atts, defaultClass ) exs : list of training examples atts : list of candidate attributes for the current node defaultClass : default class for when no examples are left initially set the majority class of all the training examples split ties in favor of -

33. Decision Tree Algorithm Node decisionTreeLearning ( exs, atts, defaultClass) { //three base cases each create leaf nodes if (empty(exs)) return new node defaultClass ; if (sameClass(exs)) return new node class(exs) ; if (empty(atts)) return new node majorityClass(exs) ; //recursive case creates sub-tree STEPS: best = chooseBestAttribute(exs, atts); // 1. tree = new node with best ; majority = majorityClass(exs); for ( each value v of best ) { // 2. v_exs = subset of exs with best == v ; // a. subtree = decisionTreeLearning( // b. v_exs, atts - best , majority); link subtree to tree and label arc v ; } return tree ; }

34. Decision Tree Algorithm How might the best attribute be chosen? Random: choose any attribute at random Least-Values: choose the attribute with the smallest number of possible values Most-Values: choose the attribute with the largest number of possible values Max-Gain: choose the attribute that has the largest expected information gain . C5.0 uses this.

35. Information Gain For a training set S = P U N , where P (positive) and N (negative) are two disjoint subsets, information gain is defined as: I(P, N) = -(P log 2 P) - (N log 2 N) where P = |P|/|S| and N = |N|/|S| note: |x| is size of set x Information gain is equivalent to a reduction in entropy , i.e. the amount of disorder in a system.

36. Information Gain Perfect Homogeneity in S : when examples are either all + or – given P = 1 (i.e. 100%) and N = 0 (i.e. 0%) I(P, N) = -(P log 2 P) - (N log 2 N) I(1, 0) = -1 log 2 1 - 0 log 2 0 = -1 (0) - ??? = -0 - 0 = 0 no disorder, no information content

37. Information Gain Perfect Balance in S : when exs. are evenly divided between + and – given P = N = ½ (i.e. 50%) I(P, N) = -(P log 2 P) - (N log 2 N) I(½, ½) = -½ log 2 ½ - ½ log 2 ½ = -½ (log 2 1 - log 2 2) - ½ (log 2 1 - log 2 2) = -½ (0 - 1) - ½ (0 - 1) = ½ + ½ = 1 max disorder, max information content

38. Information Gain I measures the information content in bits associated with a set S of exs. consisting of the disjoint subsets P of positive examples. and N of negative examples. 0 <= I(P,N) <= 1 where 0 is no info., and 1 is maximum info. its a continuous value, not binary for more see: http://www-2.cs.cmu.edu/~dst/Tutorials/Info-Theory/

39. Selecting the Best Attribute Using Information Gain Goal: Construct a small decision tree that correctly classifies the training examples. How? Select the attribute that will result in the smallest child sub-trees. Why would having low information content in the child nodes be desirable? means most, if not all, of examples in each child node are of the same class The decision tree likely to be small!

40. Selecting the Best Attribute Using Information Gain How is the information gain determined for a selected attribute A ? partition a parent node's examples by the possible values of the selected attribute assign these subsets of examples to child nodes then take the difference of the info. content of the parent node the remaining info. content in the children Gain(A) = I(P, N) – Remainder(A)

41. Selecting the Best Attribute Using Information Gain Given a set of examples: S = P U N Given a selected attribute: A having m possible values Define Remainder(A) weighted sum of the information content at each child node resulting from selecting attribute A measures the total &quot;disorder&quot; or &quot;inhomogeneity&quot; of the child nodes 0 <= Remainder(A) <= 1

42. Selecting the Best Attribute Using Information Gain Remainder(A) = q i I(P i , N i ) q i = |S i |/|S| = proportion of examples on branch i where S i = subset of S with value i, i = 1,...,m P i = |P i |/|S i | = proportion of + examples on branch i where P i = subset of S i that are + N i = |N i |/|S i | = proportion of - examples on branch i where N i = subset of S i that are - i=1 m

43. Selecting the Best Attribute Using Information Gain The best attribute of those available at a node is the attribute A with: maximum Gain(A) or equivalently, with minimum Remainder(A) since I(P,N) is constant for a given node

44. Case Studies Decision trees have been shown to be at least as accurate as human experts. Diagnosing breast cancer humans correct 65% of the time decision tree classified 72% correct BP designed a decision tree for gas-oil separation for offshore oil platforms Cessna designed a flight controller using 90,000 exs. and 20 attributes per ex.

45. Extensions to Decision Tree Learning Algorithm Evaluating Performance Accuracy: use test examples to estimate accuracy randomly partition training exs. into: TRAIN set (~80% of all training exs.) TEST set (~20% of all training exs.) generate decision tree using the TRAIN set use TEST set to evaluate accuracy accuracy = # of correct tests / total # of tests

46. Extensions to Decision Tree Learning Algorithm Noisy data could be in the examples: examples have the same attribute values, but different classifications (rare case: if(empty(atts)) ) classification is wrong attributes values are incorrect because of errors getting or preprocessing the data irrelevant attributes used in the decision-making process

47. Extensions to Decision Tree Learning Algorithm Real-valued data: pick thresholds that sort training values for attribute into equal sized bins preprocess values during learning to find the most informative thresholds Missing data: while learning: replace with most likely value while learning: use NotKnown as a value while classifying: follow arc for all values and weight each by the frequency of exs. crossing that arc

48. Extensions to Decision Tree Learning Algorithm Generation of rules: for each path from the root to a leaf the rule's antecedent is the attribute tests the consequent is the classification at leaf node if ( Size == small && Suit == hearts ) class = '+' ; Constructing theses rules yields an interpretation of the tree's meaning.

49. Extensions to Decision Tree Learning Algorithm Setting Parameters: some learning algorithms require setting learning parameters they must be set without looking at the test data one approach: use a tuning set

50. Extensions to Decision Tree Learning Algorithm Setting Parameters: Using TUNE set partition training exs. into TRAIN, TUNE, & TEST sets for each candidate parameter value, generate a decision tree using the TRAIN set use TUNE set to evaluate error rates and determine which parameter value is best compute new decision tree using selected parameter values and both TRAIN and TUNE set use TEST to compute performance accuracy

51. Extensions to Decision Tree Learning Algorithm Cross-Validation for experimental validation of performance divide all examples into N disjoint subsets E = E 1 , E 2 , ..., E N for each i = 1, ..., N let TEST set = E i and TRAIN set = E - E i compute decision tree using TRAIN set determine performance accuracy PA i using TEST set compute N-fold cross-validation estimate of performance = (PA 1 + PA 2 + ... + PA N )/N

52. Extensions to Decision Tree Learning Algorithm Overfitting meaningless regularity is found in the data irrelevant attributes confound the true, important, distinguishing features fix by pruning lower nodes in the decision tree if gain of best attribute is below a threshold, make this node a leaf rather than generating child nodes

53. Pruning Decision Trees using a Greedy Algorithm randomly partition training examples into: TRAIN set (~80% of training exs.) TUNE set (~10% of training exs.) TEST set (~10% of training exs.) build decision tree as usual using TRAIN set bestTree = decision tree produced on the TRAIN set ; bestAccuracy = accuracy of bestTree on the TUNE set ; progressMade = true; while (progressMade) { //while accuracy on TUNE improves find better tree ; //starting at root, consider various pruned versions //of the current tree and see if any are better than //the best tree found so far } return bestTree; use TEST to determine performance accuracy ;

54. Pruning Decision Trees using a Greedy Algorithm //find better tree progressMade = false; currentTree = bestTree; for ( each interiorNode N in currentTree ) { //start at root prunedTree = pruned copy of currentTree ; newAccuracy = accuracy of prunedTree on TUNE set ; if (newAccuracy >= bestAccuracy) { bestAccuracy = newAccuracy; bestTree = prunedTree; progressMade = true; } }

55. Pruning Decision Trees using a Greedy Algorithm //pruned copy of currentTree replace interiorNode N in currentTree by a leaf node label leaf node with the majorityClass among TRAIN set examples that reached node N break ties in favor of '-'

56. Summary One of the most widely used learning methods in practice Can out-perform human experts in many problems

57. Summary Strengths fast simple to implement well founded in information theory can convert result to a set of easily interpretable rules empirically valid in many commercial products handles noisy data scales well

58. Summary Weaknesses Univariate : partitions using only one attribute at a time, which limits types of possible trees large decision trees may be hard to understand requires fixed-length feature vectors non-incremental (i.e., batch method)