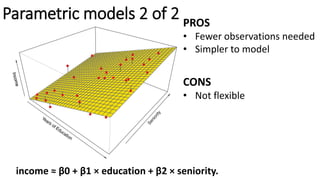
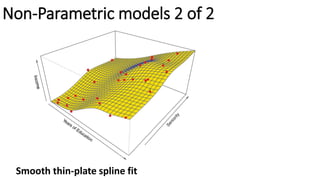
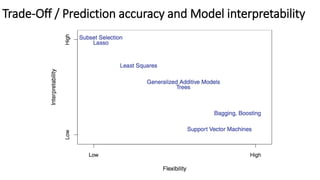
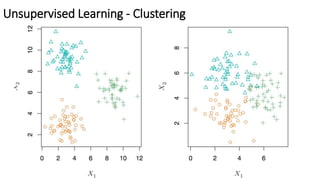
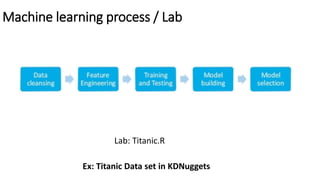
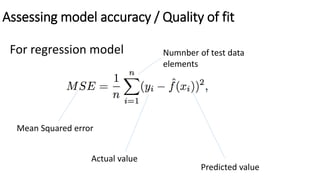
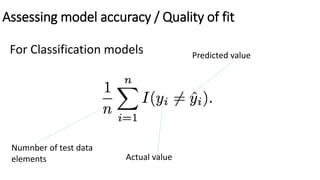
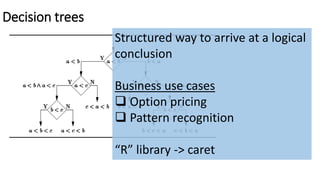
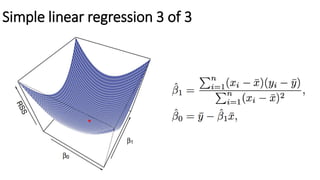
The document outlines methods of statistical learning, including parametric and non-parametric approaches, to predict outcomes based on input variables in a business context. It discusses the differences between supervised and unsupervised learning, along with various algorithms and their applications, such as regression and classification. Additionally, it covers model accuracy assessment techniques and the author's background in the technology industry.

1. Sridhar Ratakonda
Founder, PredixDATA, LLC
http://www.predixdata.com
Machine learning /
Algorithms
&
Business use cases

2. What is Statistical learning?
Let’s say you want to associate sales based on advertising channel.
Input variables “Xn” => “TV budget”, “Radio budget”, “newspaper budget”
Output variable “Y” => Sales
Y = f(X) + ͼ
Statistical learning refers to set of ways for estimating “f”

3. Estimate of “f” / Prediction
In many situations, a set of inputs X are readily
available, but the output Y cannot be easily obtained.
we can predict Y using Yˆ = ˆf(X),
fˆ = estimate for f
Yˆ = resulting prediction for Y
Ex: Predicting sales based on advertisement spend

4. Estimate of “f” / Inference 1 of 2
In some cases we want to understand how Y changes as
a function of X1,...,Xp.
• Which predictors are associated with the response?
• What is the relationship between the response and
each predictor?
• Can the relationship between Y and each predictor
be adequately summarized using a linear equation

5. Estimating “f”
Broadly speaking two methods are applied:
• Parametric
• Non-Parametric

6. Parametric models 1 of 2
Parametric methods involve a three-step model-based
approach.
I. First, make an assumption about shape, of f. For example,
one very simple assumption is that f is linear in X: f(X) = β0
+ β1X1 + β2X2 + ... + βpXp.
II. After a model has been selected, uses the training data to
fit or train the model. Solve for parameters (β0, β1, …..)
Y ≈ β0 + β1X1 + β2X2 + ... + βpXp.
III. Apply the model to predict on test data

7. Parametric models 2 of 2 PROS
• Fewer observations needed
• Simpler to model
CONS
• Not flexible
income ≈ β0 + β1 × education + β2 × seniority.

8. Non-Parametric models 1 of 2
 Non-parametric methods do not make explicit assumptions about
the functional form of f
 Instead they seek an estimate of f that gets as close to the data
points as possible
 Accurately fits known data (train data)
 Optimized to fit existing data
 High variability for true data

9. Non-Parametric models 2 of 2
Smooth thin-plate spline fit

10. Trade-Off / Prediction accuracy and Model interpretability

11. Supervised Vs. Unsupervised Learning Part 1 0f 3
Supervised learning
 For each observation of the predictor measurement(s) xi,
i = 1,...,n there is an associated response measurement yi.
 linear regression, logistic regression, boosting, support
vec- regression (SVM) etc.
 Majority of statistical models fall under “supervised mode”

12. Supervised Vs. Unsupervised Learning Part 2 0f 3
Unsupervised learning
 Unsupervised learning describes situation in which for
every observation i = 1,...,n, we observe a vector of
measurements xi but no associated response variable
 No response variable to fit
 Ex: Cluster analysis for customer segmentation

13. Unsupervised Learning - Clustering

14. Regression Vs. Classification

15. Classification model use cases
 Spam Filter
 Google news classification
 Cancel cell classification (Benign, Malignant)

16. Machine learning process / Lab
Ex: Titanic Data set in KDNuggets
Lab: Titanic.R

17. Assessing model accuracy / Quality of fit
For regression model Numnber of test data
elements
Mean Squared error
Actual value
Predicted value

18. Assessing model accuracy / Quality of fit
For Classification models Predicted value
Actual value
Numnber of test data
elements

19. Top Machine learning algorithms and business
use cases

20. Decision trees
Structured way to arrive at a logical
conclusion
Business use cases
 Option pricing
 Pattern recognition
“R” library -> caret

21. Naïve Bayes Classification
Simple probabilistic classifiers
(Baye’s theorem)
Business use cases
 Sentiment analysis (ex: FB
analyses status updates)
 Classify spam mails
“R” library -> e1071

22. Simple Linear Regression
Business use cases
 Predicting sales
 Risk assessment
“R” library -> stats

23. Logistics Regression Modeling a binomial outcome with one
or more explanatory variables
 Measures the relationship between
the categorical dependent variable and
one or more independent variables
Business use cases
 Weather prediction / Credit scoring
“R” library -> MASS

24. Support Vector Machines (SVM)
Support Vectors are co-
ordinates of individual
observation (ex: 45,150)
SVMis a frontier which best
segregates the Male from the
Females
“R” library -> e1071

25. Random Forest When you can’t think of any
algorithm use “Random Forest”
“R” library -> randomForest

26. Simple linear regression 1 of 3
Linear regression assumes that there is approximately
a linear relationship between X and Y.
Y ≈ β0 + β1X (regressing Y on X)
(Ex) Sales ≈ β0 + β1 × TV
Predicted variable SlopeY intercept

27. Simple linear regression 2 of 3
Let
Then
additional $1,000 spent on TV advertising = approximately 47.5 additional units

28. Simple linear regression 3 of 3

29. Accuracy of estimates (standard error) 1 of 2
A true relationship between Y & X takes the form
Standard error
 Standard error is introduced because model is calculated using
“available data” (sample data)
 Whole population data is not known during modeling and hence
introduction of error

30. Accuracy of estimates (standard error) 2 of 2
Standard errors can be used to compute confidence intervals
For linear regression, the 95 % confidence interval for β1, β0
approximately takes the form:
In the case of the advertising data, the 95 % confidence interval for
β0 is [6.130, 7.935] and the 95 % confidence interval for β1 is
[0.042, 0.053].

31. Interpreting standard error in regression
LAB Advertising (Summary output)

32. Accuracy of the model
 Residual Standard Error (RSE) is used to measure
accuracy of the model
 Roughly speaking, it is the average amount that the
response will deviate from the true regression line.

33. Interpreting RSE &
For advertising data RSE = 3.26 i.e. 3,260 units
difference in sales
Average sales = 14,000 units
%error = 3260/14000 = 23%
indicates variability of “Y” explained using “X”

34. ABOUT ME
25 years in Technology Industry
LinkedIn Profile:
https://www.linkedin.com/in/ratakondas/
Experience working for multiple early stage
startups and leading global teams
Current
Principal Founder – PredixDATA
(a analytics/bigdata service company)
Board of managers – Syntilla (stealth startup)