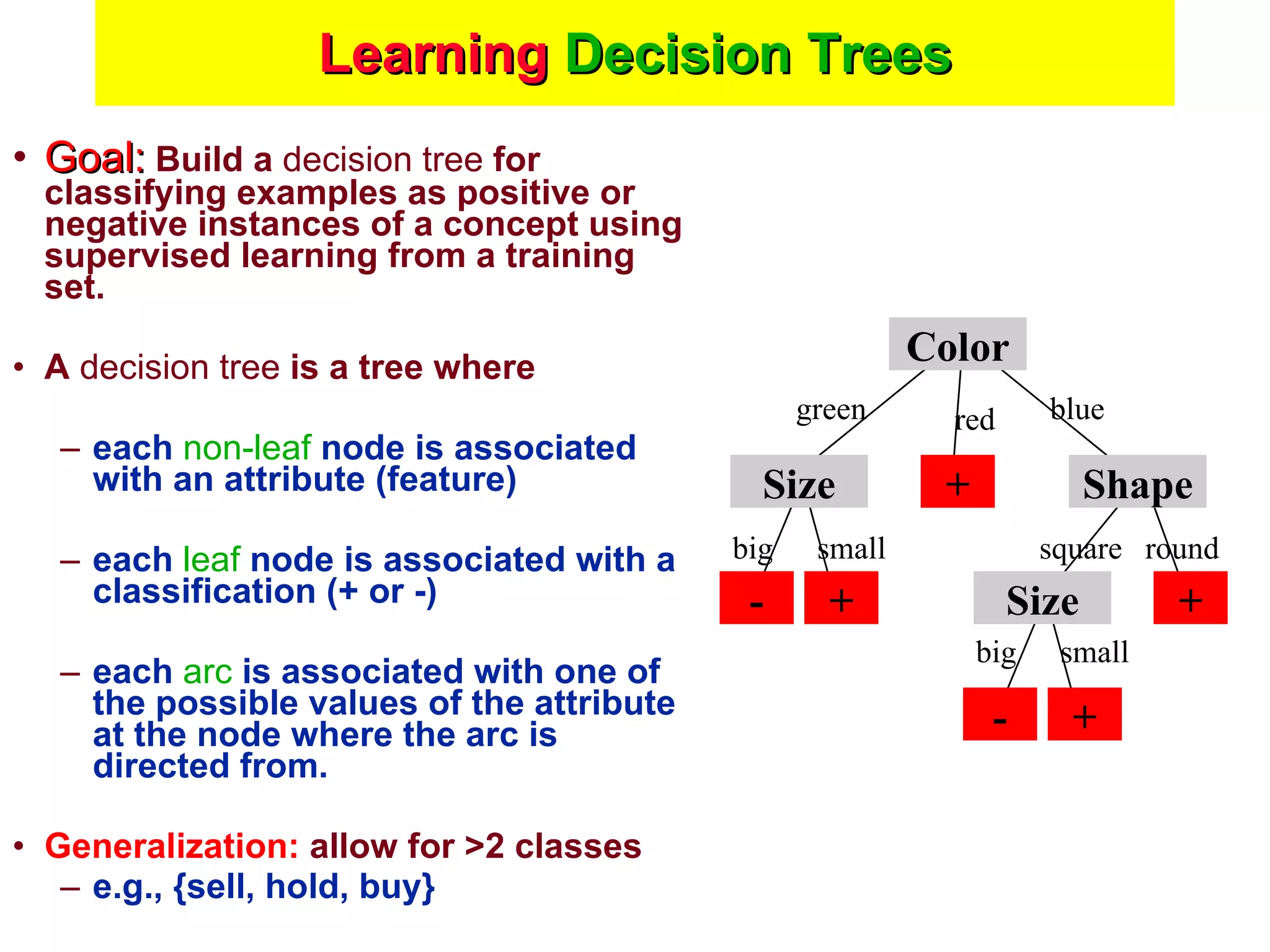
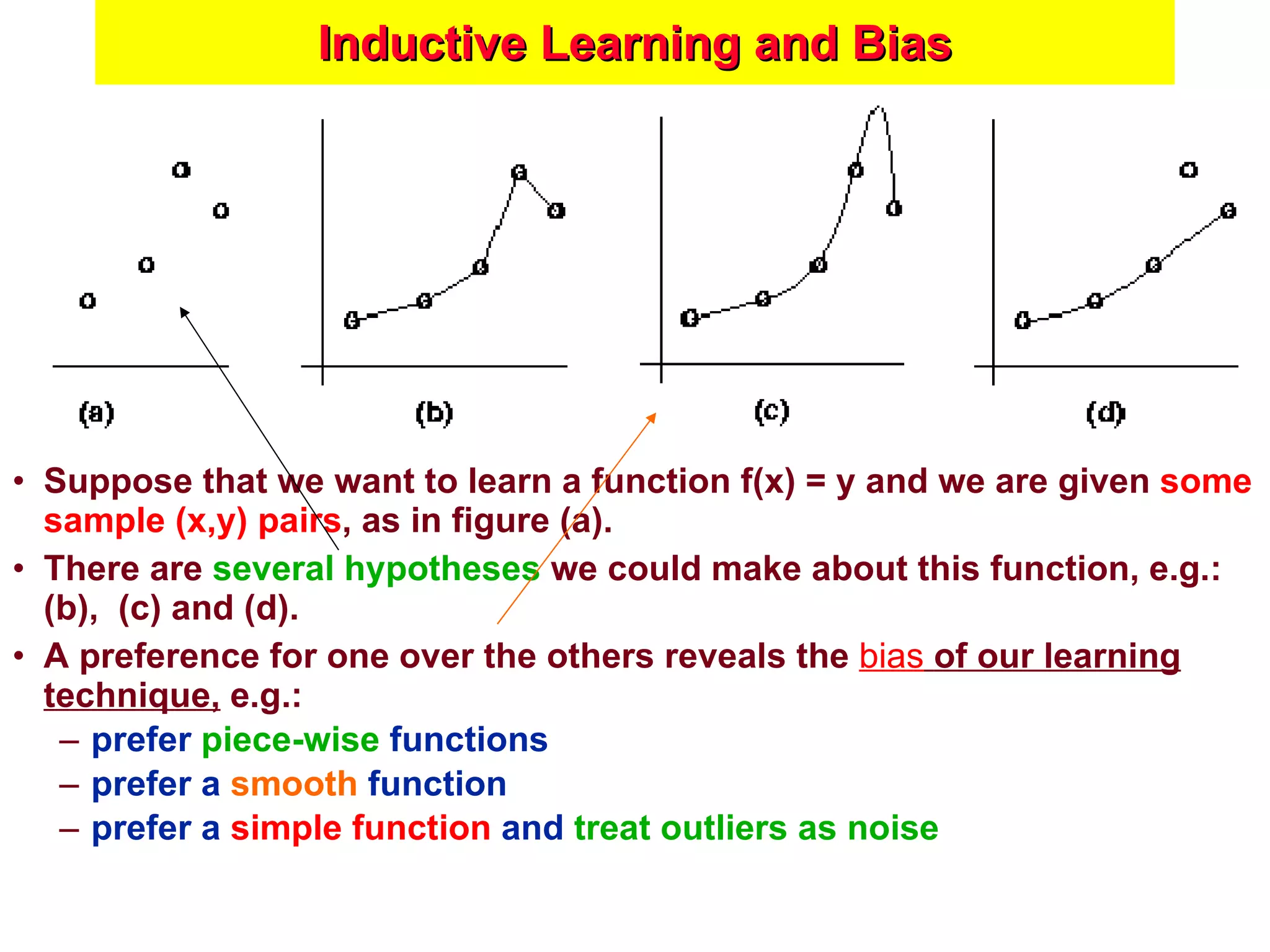
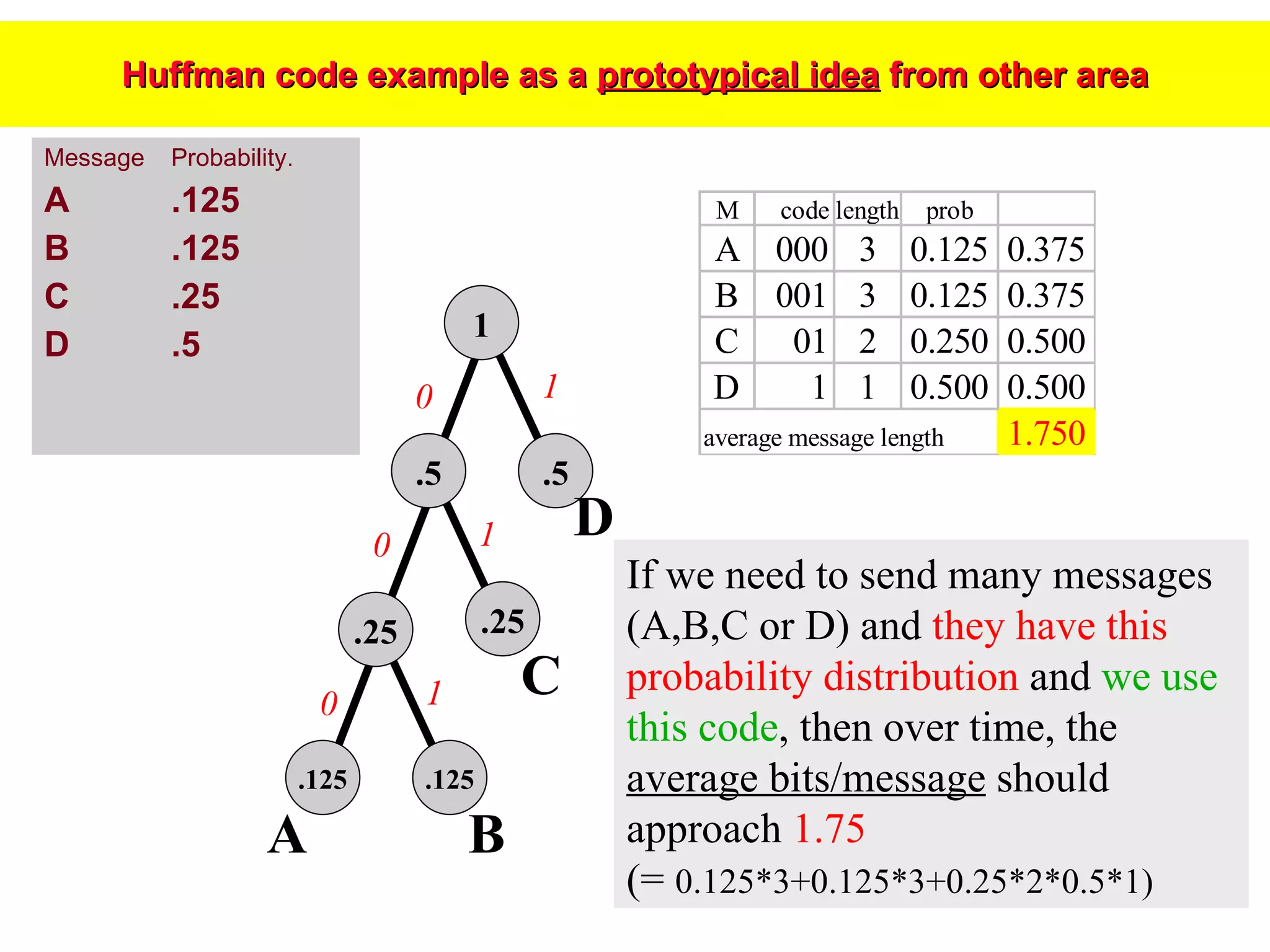
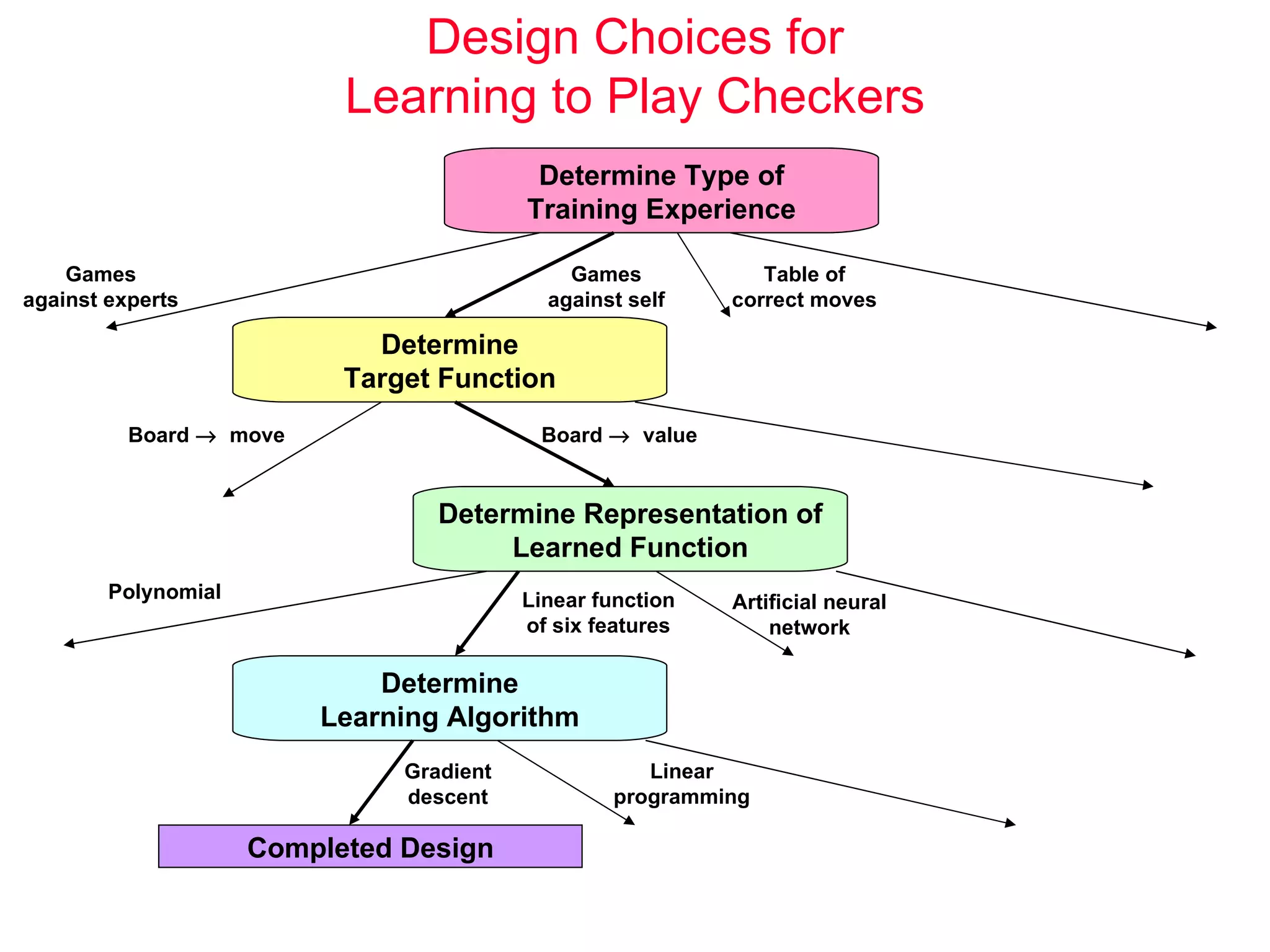
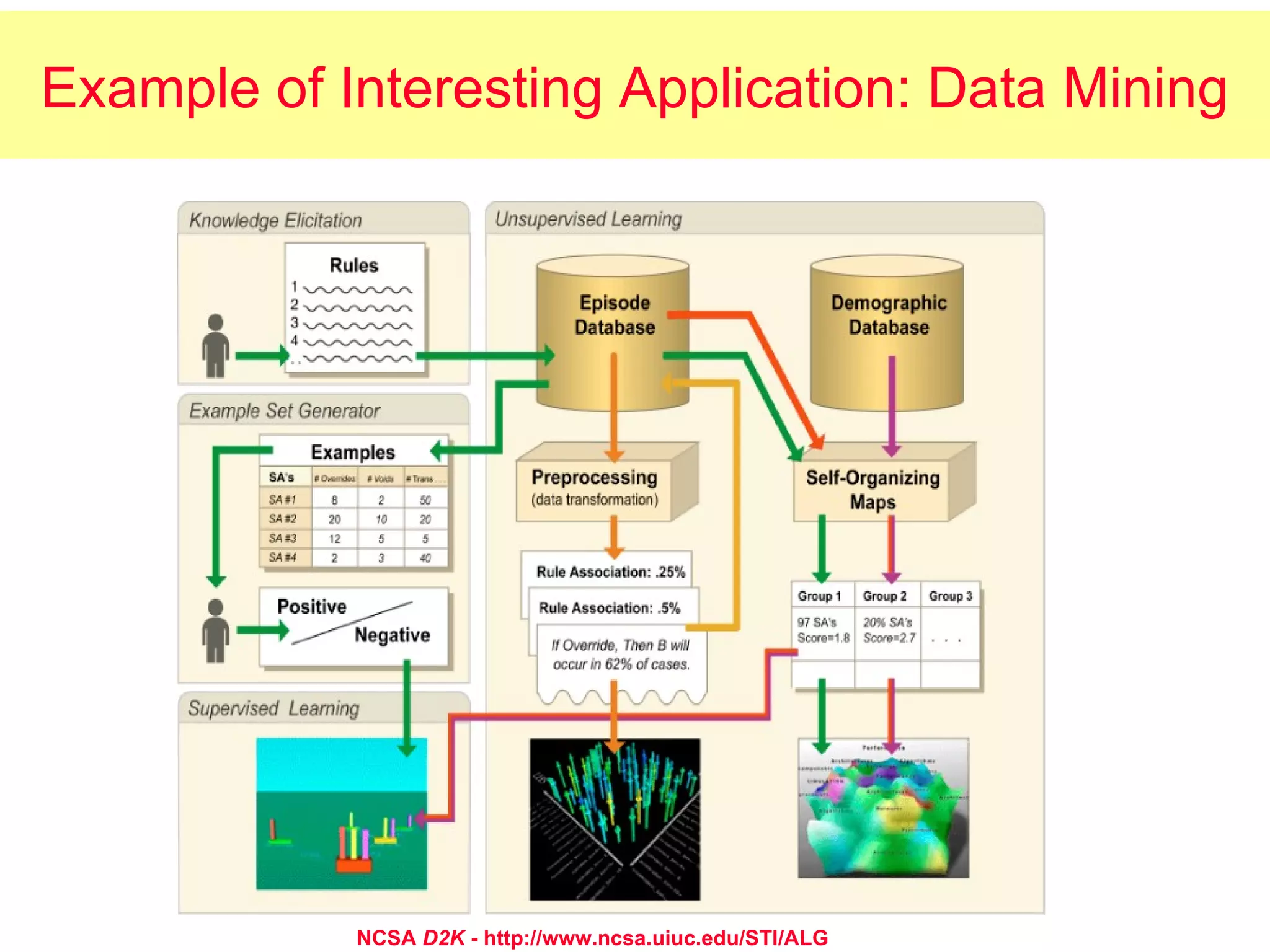
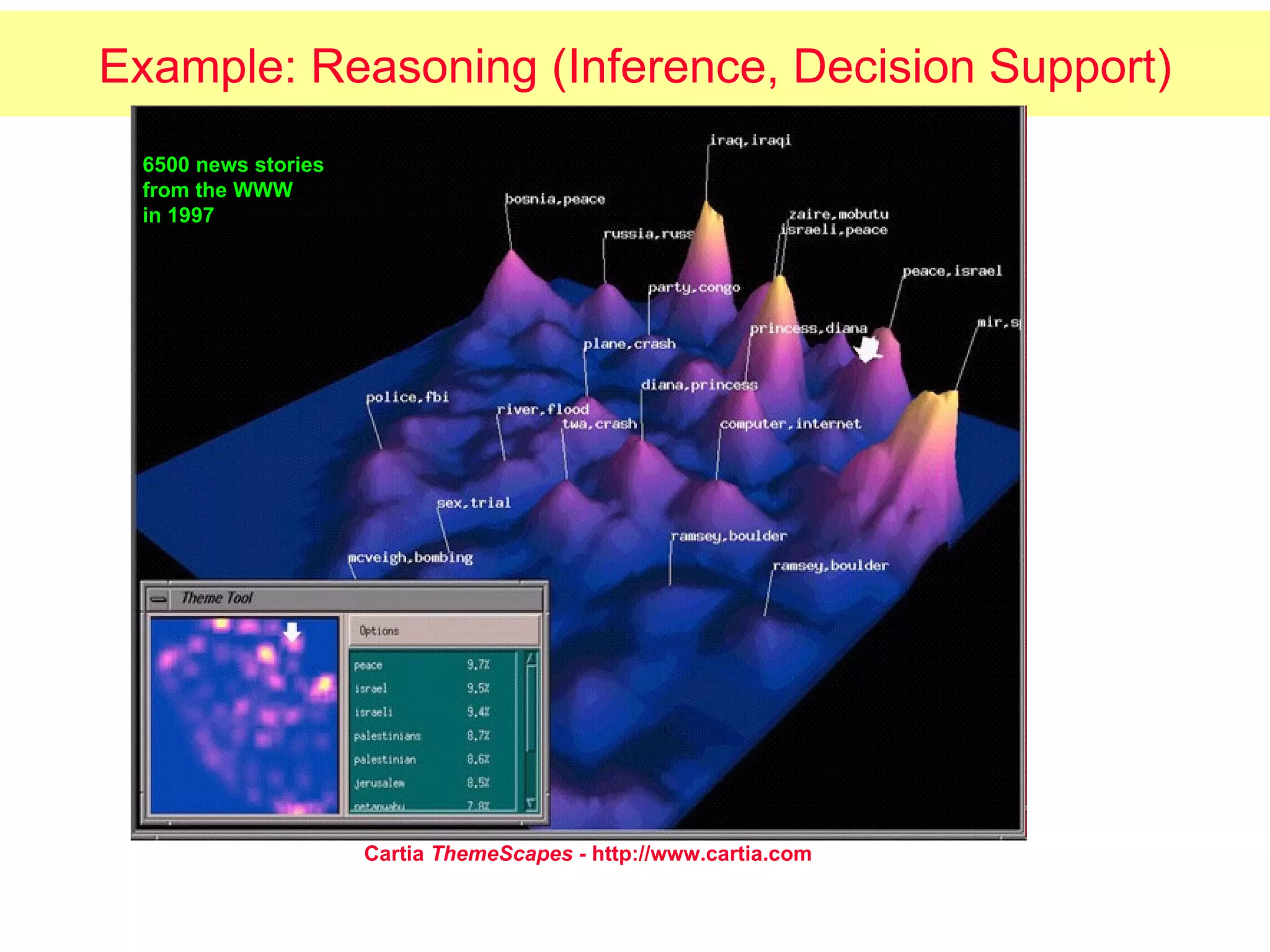
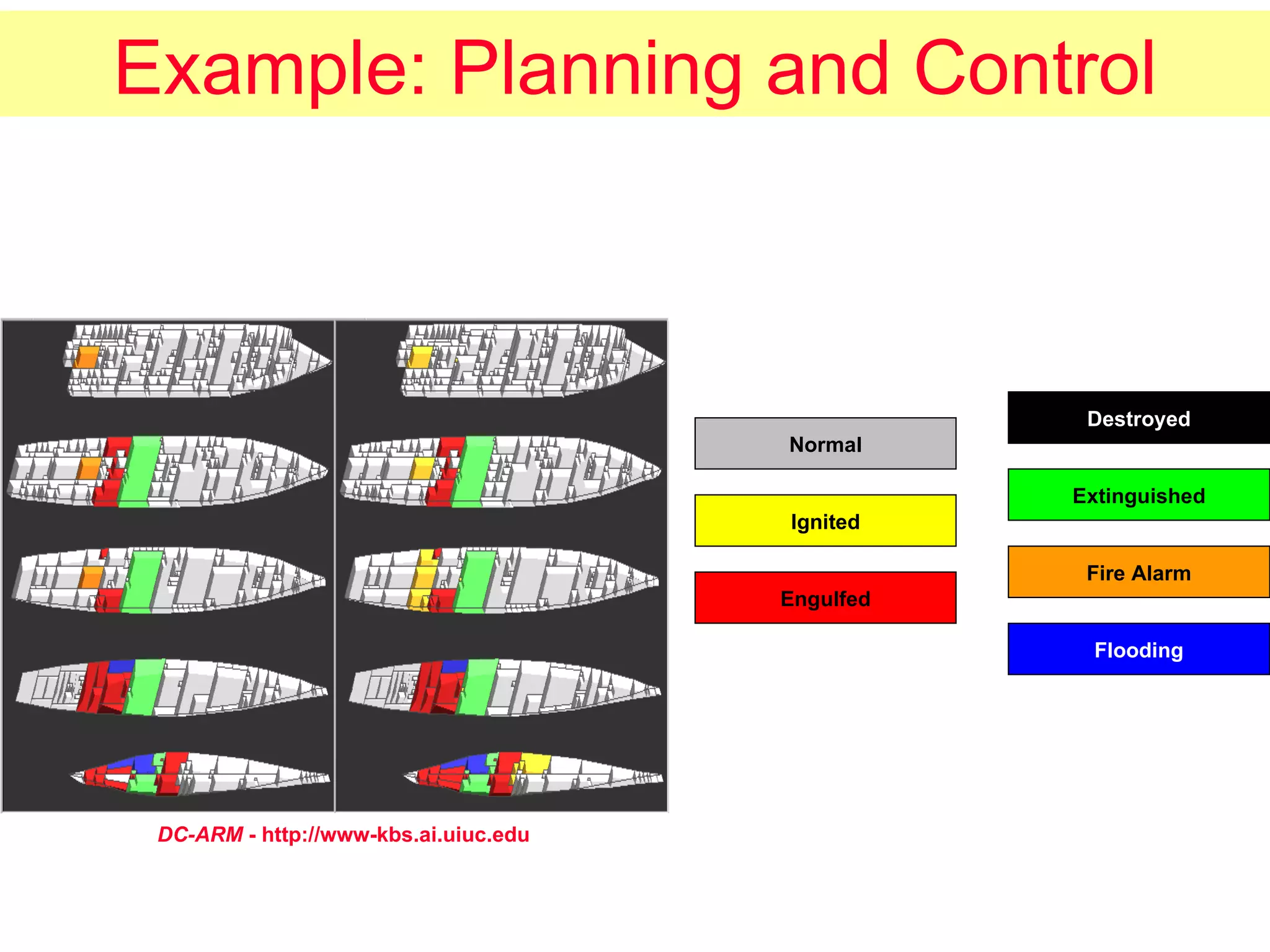
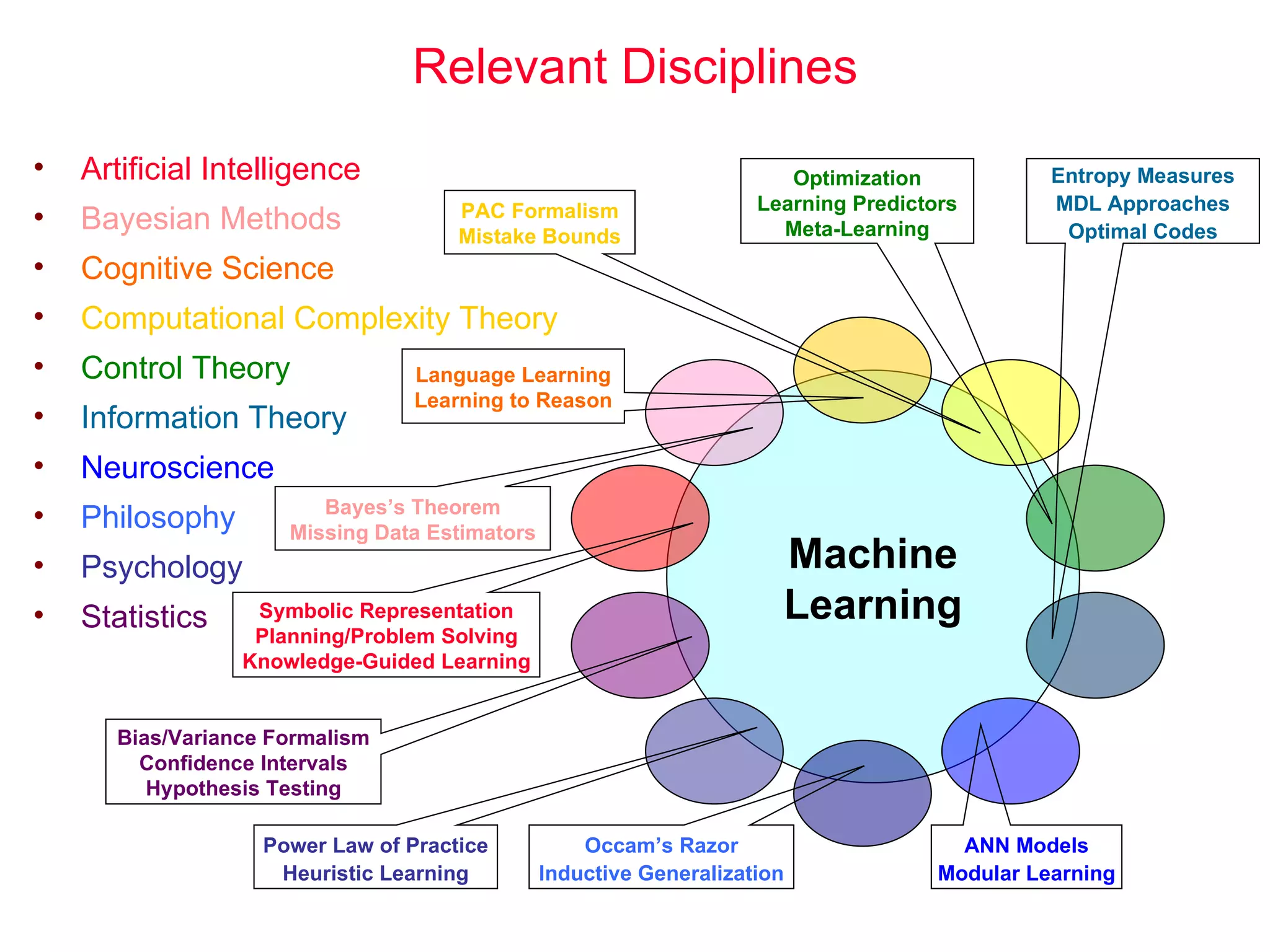
The document discusses machine learning and provides an overview of the field. It defines machine learning, explains why it is useful, and gives a brief tour of different machine learning techniques including decision trees, neural networks, Bayesian networks, and more. It also discusses some issues in machine learning like how learning problem characteristics and algorithms influence accuracy.

1. A Brief Survey of Machine Learning Used materials from: William H. Hsu Linda Jackson Lex Lane Tom Mitchell Machine Learning, Mc Graw Hill 1997 Allan Moser Tim Finin, Marie desJardins Chuck Dyer

2. ML Lectures Outline: what we will discuss? Why machine learning? Brief Tour of Machine Learning A case study A taxonomy of learning Intelligent systems engineering: specification of learning problems Issues in Machine Learning Design choices The performance element: intelligent systems Some Applications of Learning Database mining , reasoning (inference/decision support), acting Industrial usage of intelligent systems Robotics

3. What is Learning? “ Learning denotes changes in a system that ... enable a system to do the same task more efficiently the next time.” -- Herbert Simon “ Learning is constructing or modifying representations of what is being experienced.” -- Ryszard Michalski “ Learning is making useful changes in our minds.” -- Marvin Minsky definitions

4. Why Machine Learning? What ML can do? Discovers new things or structures that are unknown to humans Examples: Data mining, Knowledge Discovery in Databases Fills in skeletal or incomplete specifications about a domain Large, complex AI systems cannot be completely derived by hand They require dynamic updating to incorporate new information. Learning new characteristics : 1. expands the domain or expertise 2. lessens the "brittleness" of the system Using learning, the software agents can adapt to : to their users, to other software agents, to the changing environment.

5. Why Machine Learning? New Computational Capability Database mining: converting (technical) records into knowledge Self-customizing programs: learning news filters, adaptive monitors Learning to act: robot planning, control optimization, decision support Applications that are hard to program: automated driving, speech recognition

6. Why Machine Learning? Better Understanding of Human Learning and Teaching Understand and improve efficiency of human learning Use to improve methods for teaching and tutoring people e.g., better computer-aided instruction. ( can our robot-head teach English?) Cognitive science: theories of knowledge acquisition (e.g., through practice) Performance elements : reasoning (inference) and recommender systems Time is Right Recent progress in algorithms and theory Rapidly growing volume of online data from various sources Available computational power Growth and interest of learning-based industries (e.g., data mining/KDD)

7. A General Model of Learning Agents

8. Three Aspects of Learning Systems 1 . Models: decision trees, linear threshold units (winnow, weighted majority), neural networks, Bayesian networks (polytrees, belief networks, influence diagrams, HMMs), genetic algorithms, instance-based (nearest-neighbor) 2. Algorithms (e.g., for decision trees): ID3, C4.5, CART, OC1 3. Methodologies: supervised, unsupervised, reinforcement; knowledge-guided

9. What are the aspects of research on Learning? 1. Theory of Learning Computational learning theory (COLT): complexity, limitations of learning Probably Approximately Correct (PAC) learning Probabilistic, statistical, information theoretic results 2. Multistrategy Learning: Combining Techniques, Knowledge Sources 3. Create and collect Data: Time Series, Very Large Databases (VLDB), Text Corpora 4. Select good applications Performance element: classification, decision support, planning, control Database mining and knowledge discovery in databases (KDD) Computer inference: learning to reason

10. Some Issues in Machine Learning What Algorithms Can Approximate Functions Well? When ? How Do Learning System Design Factors Influence Accuracy? Number of training examples Complexity of hypothesis representation How Do Learning Problem Characteristics Influence Accuracy? Noisy data Multiple data sources What Are The Theoretical Limits of Learnability? How Can Prior Knowledge of Learner Help? What Clues Can We Get From Biological Learning Systems? How Can Systems Alter Their Own Representation?

11. Major Paradigms of Machine Learning Rote Learning One-to-one mapping from inputs to stored representation. "Learning by memorization.” Association-based storage and retrieval. Clustering Analogue Determine correspondence between two different representations Induction Use specific examples to reach general conclusions Discovery Unsupervised, specific goal not given Genetic Algorithms

12. Major Paradigms of Machine Learning Neural Networks Reinforcement Feedback given at end of a sequence of steps. Feedback can be positive or negative reward Assign reward to steps by solving the credit assignment problem — which steps should receive credit or blame for a final result?

13. The Inductive Learning Problem Induce rules that extrapolate from a given set of examples These rules should make “accurate” predictions about future examples. Supervised versus Unsupervised learning Learn an unknown function f(X) = Y, where: X is an input example and Y is the desired output . Supervised learning implies we are given a training set of (X, Y) pairs by a "teacher.“ Unsupervised learning means we are only given the Xs and some (ultimate) feedback function on our performance.

14. The Inductive Learning Problem Concept learning Called also Classification Given a set of examples of some concept/class/category, determine if a given example is an instance of the concept or not. If it is an instance, we call it a positive example . If it is not, it is called a negative example .

15. Supervised Concept Learning Given a training set of positive and negative examples of a concept Usually each example has a set of features/attributes Construct a description that will accurately classify whether future examples are positive or negative. That is, learn some good estimate of function f given a training set {(x1, y1), (x2, y2), ..., (xn, yn)} where each yi is either + (positive) or - (negative). f is a function of the features/attributes

16. Inductive Learning Framework Raw input data from sensors are preprocessed to obtain a feature vector , X, that adequately describes all of the relevant features for classifying examples. Each x is a list of (attribute, value) pairs. For example, X = [Person:Sue, EyeColor:Brown, Age:Young, Sex:Female] The number and names of attributes (aka features ) is fixed (positive, finite). Each attribute has a fixed, finite number of possible values. Each example can be interpreted as a point in an n-dimensional feature space , where n is the number of attributes.

17. Inductive Learning by Nearest-Neighbor Classification One simple approach to inductive learning is to save each training example as a point in feature space Classify a new example by giving it the same classification (+ or -) as its nearest neighbor in Feature Space. 1. A variation involves computing a weighted sum of class of a set of neighbors where the weights correspond to distances 2. Another variation uses the center of class The problem with this approach is that it doesn't necessarily generalize well if the examples are not well "clustered."

18. Learning Decision Trees Goal: Build a decision tree for classifying examples as positive or negative instances of a concept using supervised learning from a training set. A decision tree is a tree where each non-leaf node is associated with an attribute (feature) each leaf node is associated with a classification (+ or -) each arc is associated with one of the possible values of the attribute at the node where the arc is directed from. Generalization: allow for >2 classes e.g., {sell, hold, buy} Color Shape Size + + - Size + - + big big small small round square red green blue

19. Preference Bias: Ockham's Razor Aka Occam’s Razor , Law of Economy, or Law of Parsimony Principle stated by William of Ockham (1285-1347/49), a scholastic, that “ non sunt multiplicanda entia praeter necessitatem” or, entities are not to be multiplied beyond necessity. The simplest explanation that is consistent with all observations is the best. Therefore, the smallest decision tree that correctly classifies all of the training examples is best. Finding the provably smallest decision tree is NP-Hard Therefore we do not construct the absolute smallest tree consistent with the training examples. We construct a tree that is pretty small .

20. Inductive Learning and Bias Suppose that we want to learn a function f(x) = y and we are given some sample (x,y) pairs , as in figure (a). There are several hypotheses we could make about this function, e.g.: (b), (c) and (d). A preference for one over the others reveals the bias of our learning technique, e.g.: prefer piece-wise functions prefer a smooth function prefer a simple function and treat outliers as noise

21. Example of using probabilities to create trees: Huffman code In 1952 MIT student David Huffman devised, in the course of doing a homework assignment , an elegant coding scheme This scheme is optimal in the case where all symbols’ probabilities are integral powers of 1/2. A Huffman code can be built in the following manner: 1. Rank all symbols in order of probability of occurrence. 2. Successively combine the two symbols of the lowest probability to form a new composite symbol; eventually we will build a binary tree where each node is the probability of all nodes beneath it. 3. Trace a path to each leaf, noticing the direction at each node.

22. Huffman code example as a prototypical idea from other area Message Probability. A .125 B .125 C .25 D .5 If we need to send many messages (A,B,C or D) and they have this probability distribution and we use this code , then over time, the average bits/message should approach 1.75 (= 0.125*3+0.125*3+0.25*2*0.5*1) .5 .5 1 .125 .125 .25 A C B D .25 0 1 0 0 1 1

23. If a set T of records is partitioned into disjoint exhaustive classes (C1,C2,..,Ck) on the basis of the value of the categorical attribute, then the information needed to identify the class of an element of T is Info(T) = I(P) where P is probability distribution of partition (C1,C2,..,Ck): P = (|C1|/|T|, |C2|/|T|, ..., |Ck|/|T|) If we partition T w.r.t attribute X into sets {T1,T2, ..,Tn} then the information needed to identify the class of an element of T becomes the weighted average of the information needed to identify the class of an element of Ti, i.e. the weighted average of Info(Ti): Info(X,T) =  |Ti|/|T| * Info(Ti) =  |Ti|/|T| * log |Ti|/|T|

24. Gain Consider the quantity Gain(X,T) defined as Gain(X,T) = Info(T) - Info(X,T) This represents the difference between information needed to identify an element of T and information needed to identify an element of T after the value of attribute X has been obtained, that is, this is the gain in information due to attribute X. We can use this to rank attributes and to build decision trees where at each node is located the attribute with greatest gain among the attributes not yet considered in the path from the root. The intents of this ordering are twofold: 1. To create small decision trees so that records can be identified after only a few questions. 2. To match a hoped for minimality of the process represented by the records being considered (Occam's Razor). We will use this idea to build decision trees, ID3

25. Rule and Decision Tree Learning Example: Rule Acquisition from Historical Data Data Patient 103 (time = 1): Age 23, First-Pregnancy: no, Anemia: no, Diabetes: no, Previous-Premature-Birth: no, Ultrasound: unknown , Elective C-Section: unknown , Emergency-C-Section: unknown Patient 103 (time = 2): Age 23, First-Pregnancy: no, Anemia: no, Diabetes: yes , Previous-Premature-Birth: no, Ultrasound: abnormal , Elective C-Section: no, Emergency-C-Section: unknown Patient 103 (time = n): Age 23, First-Pregnancy: no, Anemia: no, Diabetes: no, Previous-Premature-Birth: no, Ultrasound: unknown , Elective C-Section: no, Emergency-C-Section: YES Learned Rule IF no previous vaginal delivery , AND abnormal 2nd trimester ultrasound , AND malpresentation at admission , AND no elective C-Section THEN probability of emergency C-Section is 0.6 Training set: 26/41 = 0.634 Test set: 12/20 = 0.600

26. Neural Network Learning A utonomous L earning V ehicle I n a N eural N et (ALVINN): Pomerleau et al http://www.cs.cmu.edu/afs/cs/project/alv/member/www/projects/ALVINN.html Drives 70mph on highways

27. Specifying A Learning Problem Learning = Improving with Experience at Some Task Improve over task T , with respect to performance measure P , based on experience E . Example: Learning to Play Checkers T : play games of checkers P : percent of games won in world tournament E : opportunity to play against self Refining the Problem Specification: Issues What experience? What exactly should be learned? How shall it be represented ? What specific algorithm to learn it? Defining the Problem Milieu Performance element: How shall the results of learning be applied? How shall the performance element be evaluated? The learning system?

28. Example : Learning to Play Checkers Type of Training Experience Direct or indirect? Teacher or not? Knowledge about the game (e.g., openings/endgames)? Problem: Is Training Experience Representative (of Performance Goal)? Software Design Assumptions of the learning system: legal move generator exists Software requirements: generator, evaluator(s), parametric target function Choosing a Target Function ChooseMove: Board  Move (action selection function, or policy ) V: Board  R (board evaluation function) Ideal target V ; approximated target Goal of learning process: operational description (approximation) of V

29. A Target Function for Learning to Play Checkers Possible Definition If b is a final board state that is won, then V(b) = 100 If b is a final board state that is lost, then V(b) = -100 If b is a final board state that is drawn, then V(b) = 0 If b is not a final board state in the game, then V(b) = V(b’) where b’ is the best final board state that can be achieved starting from b and playing optimally until the end of the game Correct values, but not operational Choosing a Representation for the Target Function Collection of rules? Neural network? Polynomial function (e.g., linear, quadratic combination) of board features? Other? A Representation for Learned Function bp/rp = number of black/red pieces; bk/rk = number of black/red kings; bt/rt = number of black/red pieces threatened (can be taken on next turn)

30. A Training Procedure for Learning to Play Checkers Obtaining Training Examples the target function the learned function the training value One Rule For Estimating Training Values: Choose Weight Tuning Rule Least Mean Square (LMS) weight update rule: REPEAT Select a training example b at random Compute the error(b) for this training example For each board feature f i , update weight w i as follows: where c is a small, constant factor to adjust the learning rate

31. Design Choices for Learning to Play Checkers Completed Design Determine Type of Training Experience Games against experts Games against self Table of correct moves Determine Target Function Board  value Board  move Determine Representation of Learned Function Polynomial Linear function of six features Artificial neural network Determine Learning Algorithm Gradient descent Linear programming

32. Example of Interesting Application: Data Mining Database Mining NCSA D2K - http://www.ncsa.uiuc.edu/STI/ALG

33. Example: Reasoning (Inference, Decision Support) Cartia ThemeScapes - http://www.cartia.com 6500 news stories from the WWW in 1997

34. Example: Planning and Control Normal Ignited Engulfed Destroyed Extinguished Fire Alarm Flooding DC-ARM - http://www-kbs.ai.uiuc.edu

35. Relevant Disciplines Artificial Intelligence Bayesian Methods Cognitive Science Computational Complexity Theory Control Theory Information Theory Neuroscience Philosophy Psychology Statistics Machine Learning Symbolic Representation Planning/Problem Solving Knowledge-Guided Learning Bayes’s Theorem Missing Data Estimators PAC Formalism Mistake Bounds Language Learning Learning to Reason Optimization Learning Predictors Meta-Learning Entropy Measures MDL Approaches Optimal Codes ANN Models Modular Learning Occam’s Razor Inductive Generalization Power Law of Practice Heuristic Learning Bias/Variance Formalism Confidence Intervals Hypothesis Testing