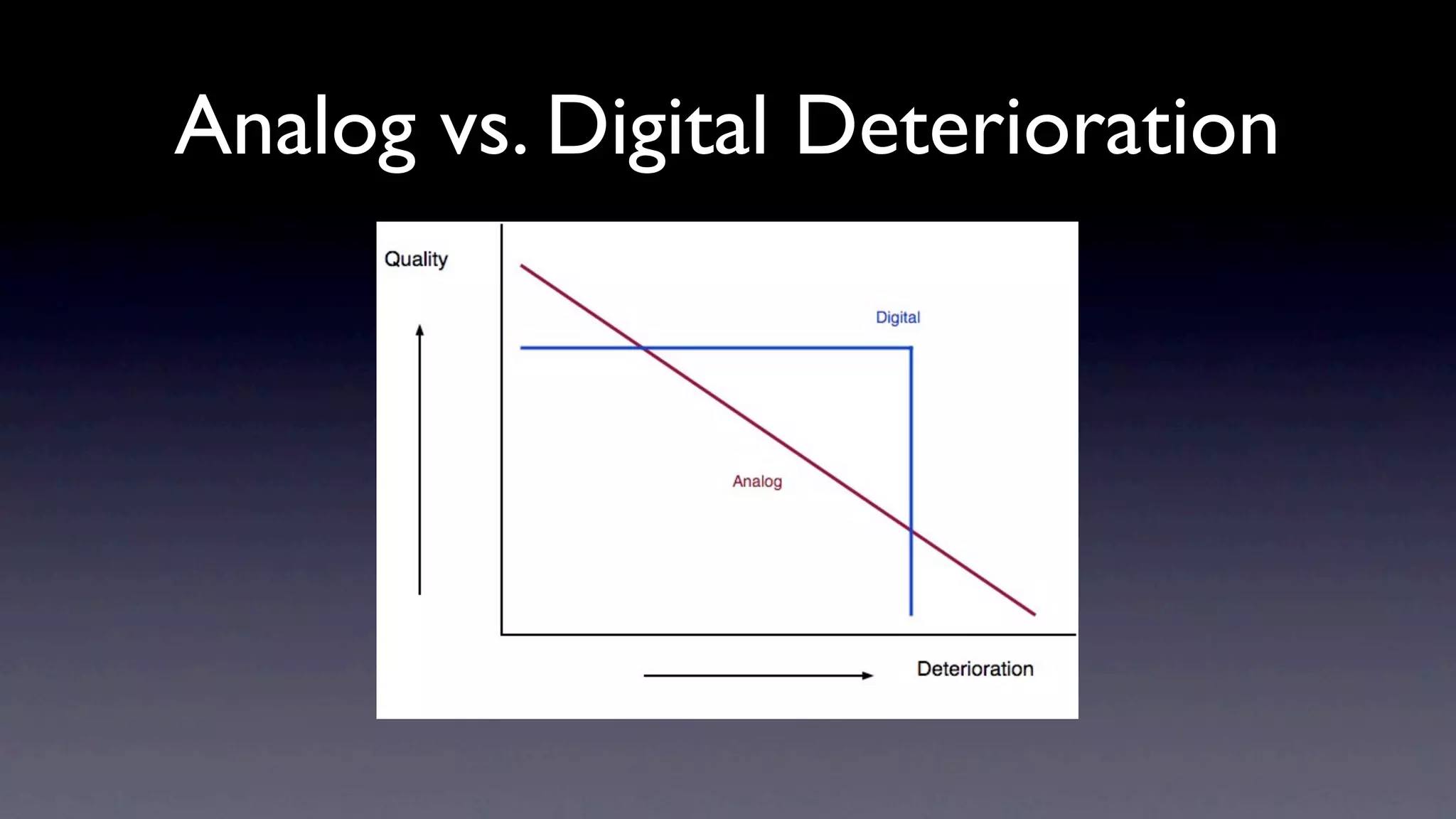
This document discusses key concepts in digital audio, including: 1) Digital audio is discrete in both time and amplitude, where analog is continuous. Sampling converts an analog signal to digital by taking discrete time and amplitude samples. 2) For lossless sampling, the sampling rate must be at least twice the bandwidth of the analog signal to avoid aliasing. 3) Quantization converts the sampled amplitude values to discrete digital values. More bits provide higher resolution and dynamic range but introduce quantization error and noise. 4) Digital audio can be transmitted via various standards like AES/EBU and S/PDIF using pulse code modulation to encode the digital samples into a binary data stream. O

1. MUSC 365
Basics of Digital Audio Module (original)

2. Analog = continuous
• continuous time and amplitude

3. Digital = discrete
• is discrete time and amplitude

4. Sampling Theory

5. Sampling
• making discrete Time
• A signal of bandwidth BW may be LOSSLESSLY sampled if the
sampling rate Fs >= 2BW

6. Sampling
• Amplitude is held (sampled) only at certain times
• Input must be bandlimited to half the sampling rate

7. Nyquist Frequency
• half the sampling frequency
• Fs/2

8. Critical sampling
• When a signal is sampled at exactly twice its highest frequency
• Never done in audio

9. Sampling Rate
• High
• Large guard band
• Allows varispeed
• Low
• Reduce transmission and storage BW

10. Sampling
• A band limited waveform amplitude modulates an impulse train.
• The spectrum of an impulse train is sinewaves @ multiples of Fs
• Modulated spectrum is waveform spectrum (bandlimited) repeated
around multiples of Fs (with upper and lower sidebands)
• If impulses have some width, then the total spectrum is superimposed
with the |Sin (x)/x| curve

11. Aliasing
• Input signal must be bandlimited
• If it is not, sampling will cause the first lower sideband to fold back
into the signal
• Inputs frequencies above Fs/2 are folded back into audio band
• Wagon wheel analogy in film
• A 7 kHz wave sampled @ 10kHz looks just like a 3 kHz wave

12. Sample & Hold
• Must acquire analog input amplitude at sample time and hold it long
enough for it to be quantized
• Sampled analog waveform has greater bandwidth than original input.
This is inefficient, so amplitude is Quantized and Coded.

13. Encoding/Modulation

14. Pulse Code Modulation (PCM)
• Binary Code is transmitted

15. Quantization
• making discrete Amplitude
• Peak S/E(dB) = 6.02n + 1.76
• 1.76 factor based on sinusoidal input
• Adding bit increases S/N by 6dB
• Number of bits determines resolution

16. Dynamic Range
• 8 bits = 28 = 256 = 48dB
• 12 bits = 212 = 4,096 = 72dB
• 16 bits = 216 = 65,536 = 96dB
• 20 bits = 220 = 1,048,576 = 120dB
• 24 bits = 224 = 16,777,216 = 144dB

17. Dynamic Range
• S/E power ratio increases exponentially with data bandwidth
• (one additional bit is double the accuracy)
• assumes equal distribution (large signal)

18. Incredible accuracy
• Image a stack of paper 22 feet high. The thickness of a sheet of paper
is the accuracy of a 16bit quantization interval!
• Image a stack of paper a mile high. The thickness of a sheet of paper is
the accuracy of a 24bit quantization interval!

19. Quantization Error
• Distortion power relative to number of intervals, independent of
amplitude of signal
• No input, no error
• Perceptively changes with input type and level
• Error is +/- 1/2 Q with a rectangular PDF (equal chance)
• High level signal has un-correlated error

20. Types of error
• Overload Noise (If input > MSB)
• Over lights on equipment
• Random Noise (large input)
• White noise (rectangular, not Gaussian p.d.f), masked by signal
• Granulation distortion (Very low level input)

21. Quantization Error
• Quantization noise is not random, but based on signal.
• Distortion produces harmonics which can alias
• Multiple input freq. can cause intermodulation distortion
• Quantization error can create Aliasing (frequencies not present in
source) even though it occurs after the sample process

22. Idle channel Noise/Hunting noise
• Input signal below LSB, but low freq. information (rumble) moves it
across quantizing intervals, the signal (and noise) will come and go

23. Distortion, not noise
• Peak to peak = ±1/2 Quantization interval (Q)
• An ideal quantizer is by definition non-linear and will cause
distortion!!

24. Quantizing
• Held amplitude is measured and assigned the closest number
• 2n steps, where n = number of bits
• approximately 6dB of dynamic range per bit

25. Transmission
• AES/EBU
• S/PDIF
• TDIF

26. Metering
• 0dBFS (reference is when all codes are being used – Full Scale)
• Overload
• Output is at full scale for many consecutive samples

27. Dither
• Noise added to the signal to de-correlate the signal from the
quantizer

28. Pro
• Randomizes granulation distortion, changing it to white noise
• encodes low-level signals via PWM
• ear averages PWM signal to resolve signal
• With dither, resolution is below least significant bit!

29. Con
• Raises noise floor slightly

30. ADC Process
• Analog-to-Digital conversion
• Anti-alias filter
• sample & hold
• quantizer (with Dither)

31. Oversampling
• to ease the requirements
• of the anti-alias filter and
• the accuracy of the quantizer
• we trade amplitude accuracy for time accuracy
• sample crude, but fast

32. Oversampling
• gentle analog anti-alias filter
• High Fs
• Digital filter (anti-alias) and downsample
• Digital filter easier than analog

33. Dynamic Range
• S/N = 6.02(#of bits + 0.5* #of octaves oversampling) + 1.76

34. Analog vs. Digital Deterioration
• In Analog, noise steadily deteriorates the signal-to-noise ratio
• In Digital, we reach a point of catastrophic failure, when the data can
no longer be received correctly

35. Analog vs. Digital Deterioration