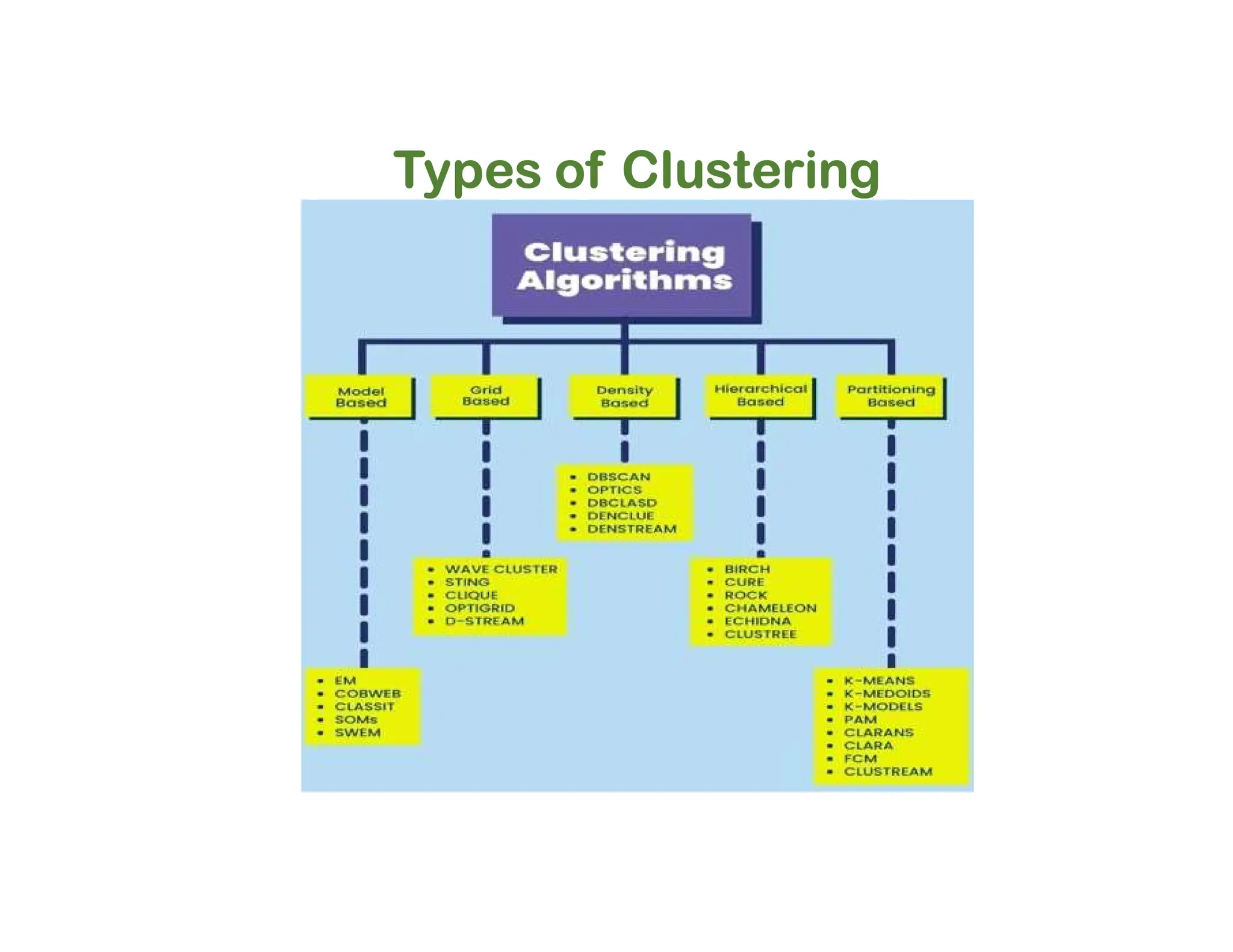
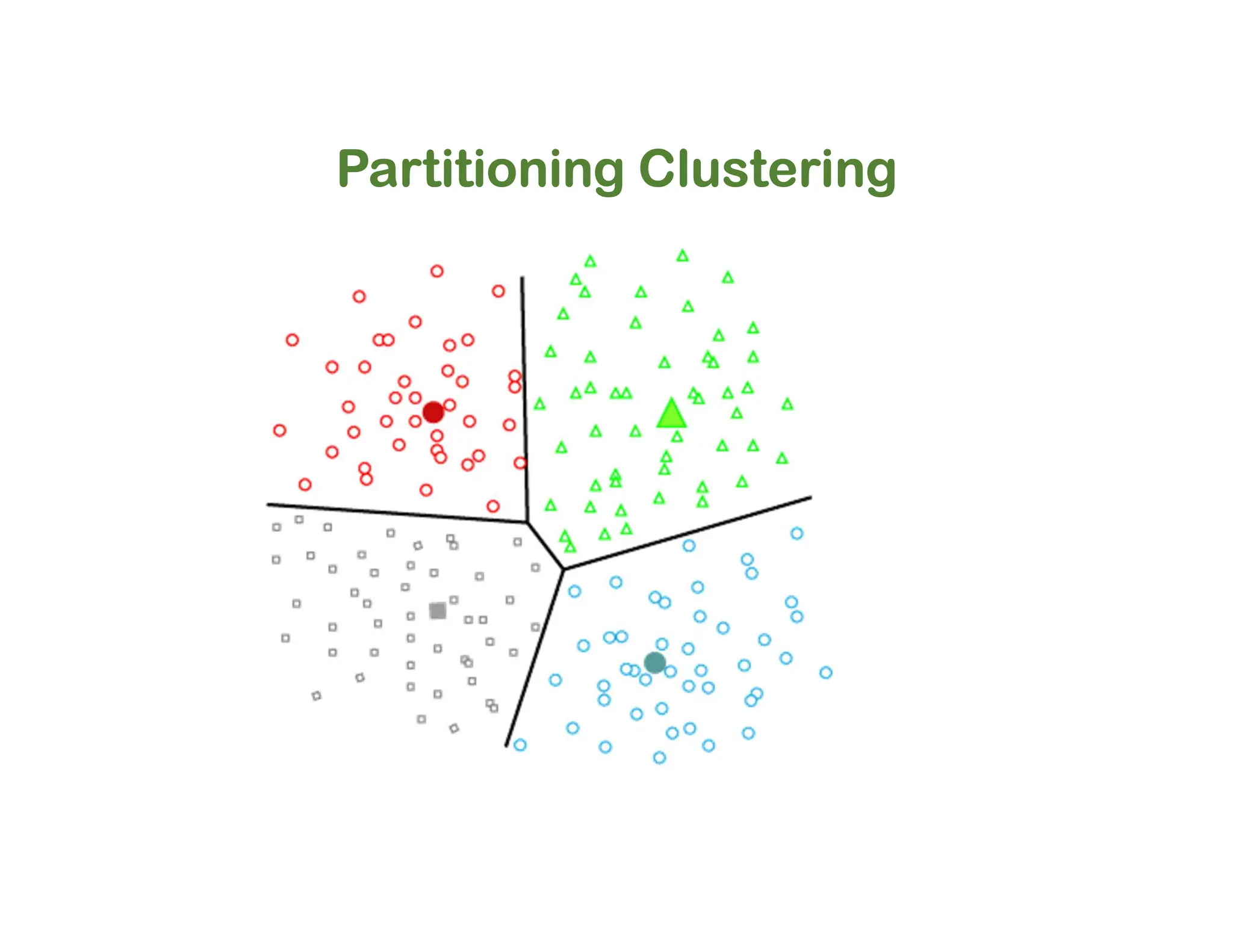
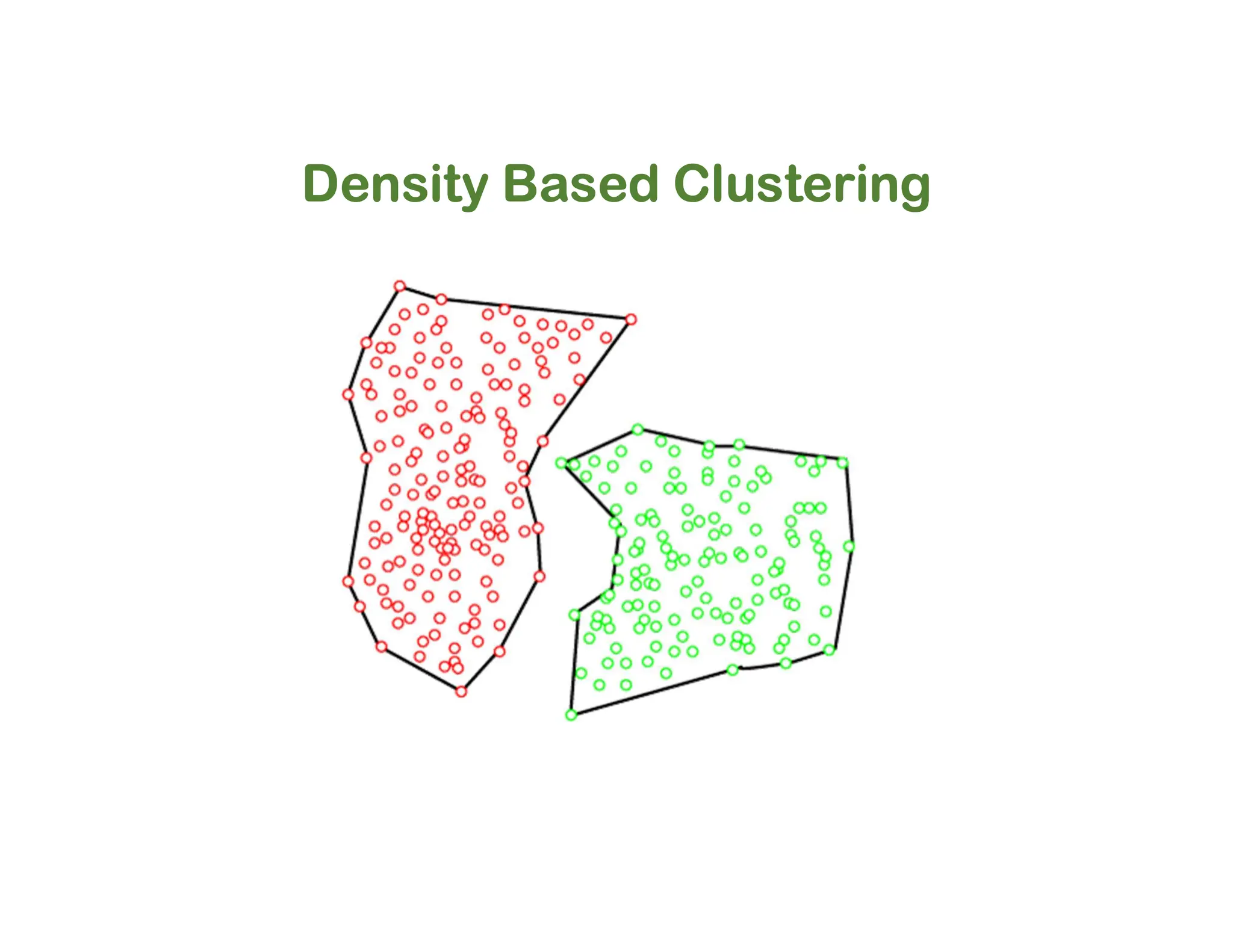
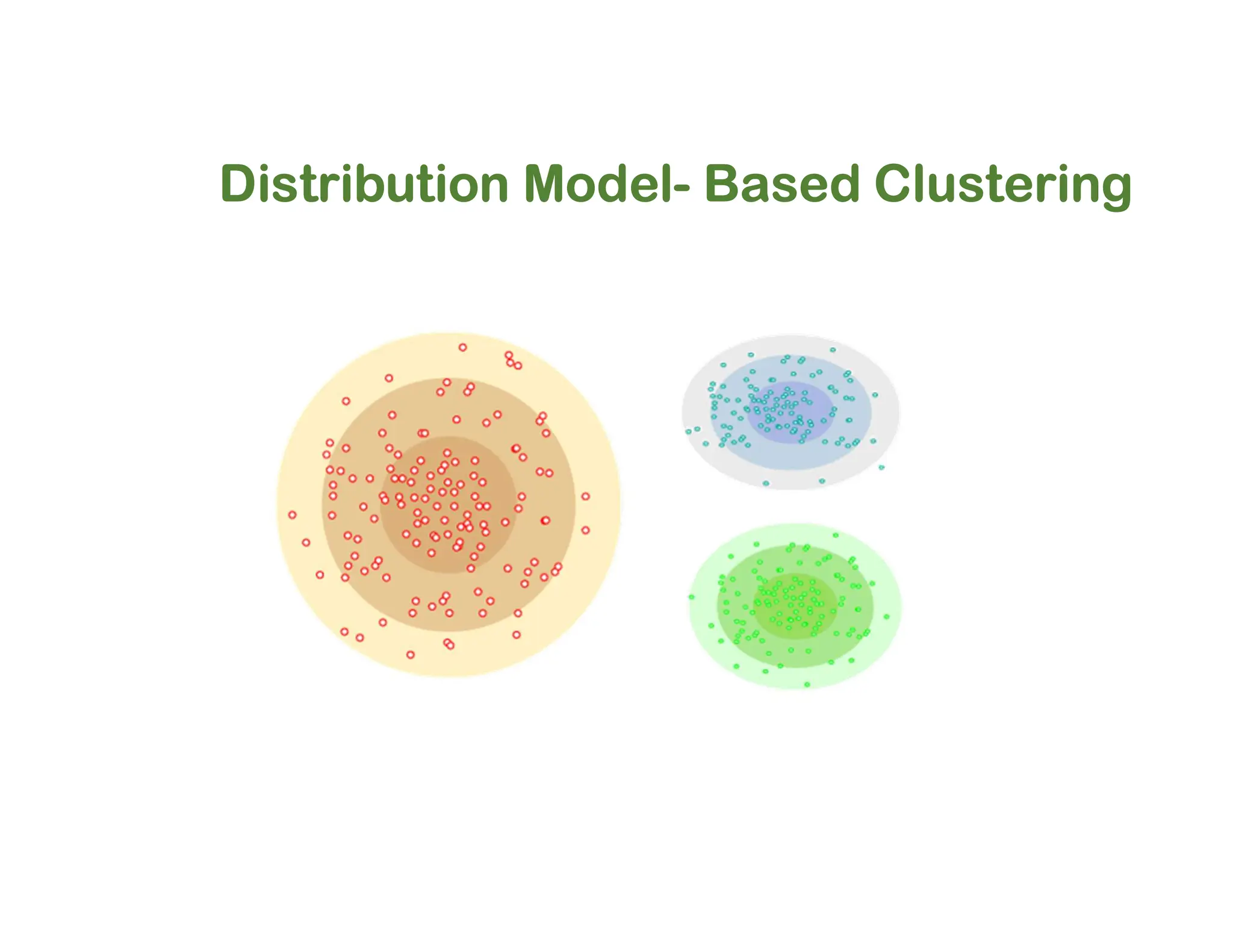
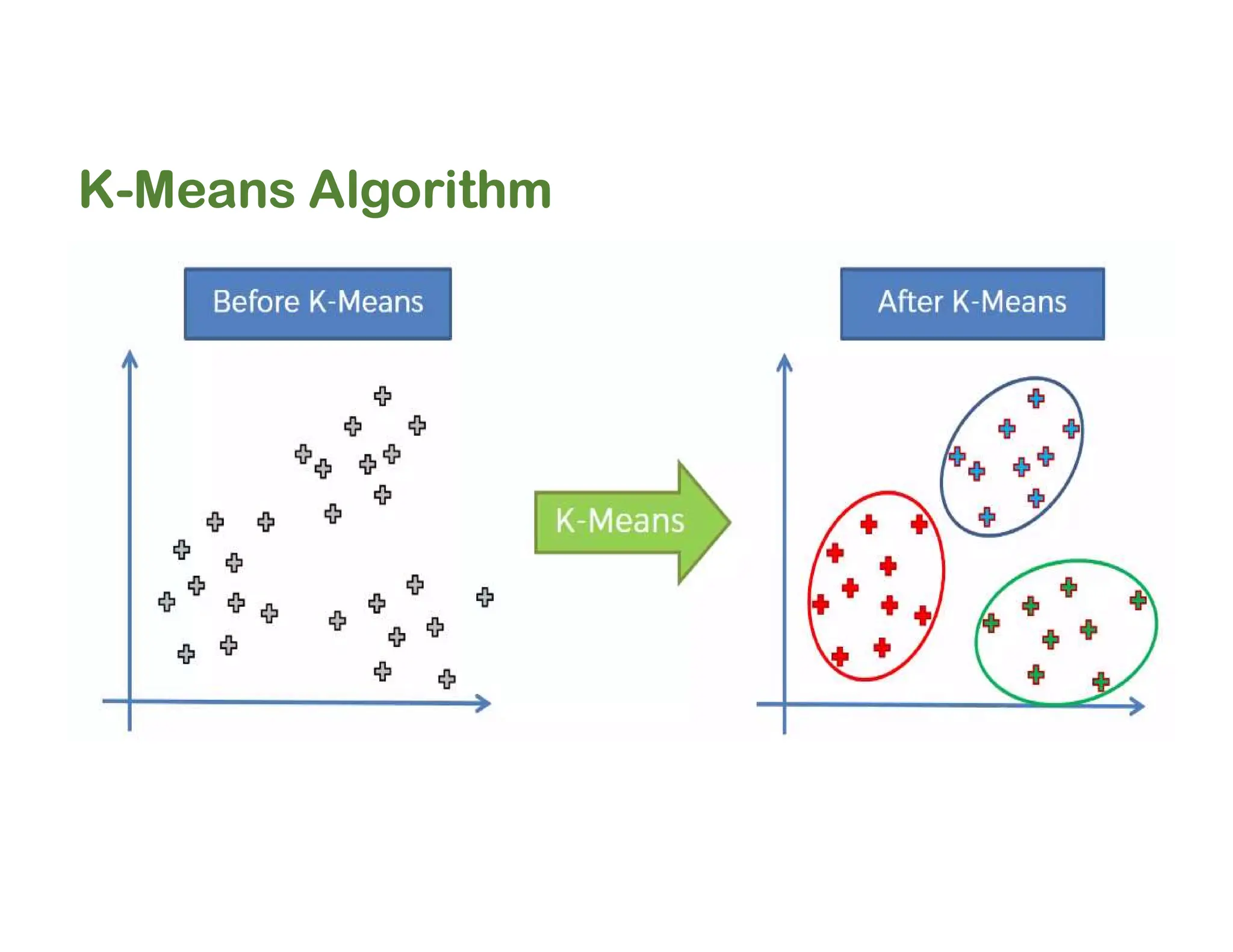
The document discusses clustering methods, including k-means and hierarchical clustering, highlighting their differences and various algorithms used. It details applications of clustering in areas such as customer segmentation and anomaly detection, and provides code examples for implementing k-means clustering and hierarchical clustering using Python. Additionally, it explains techniques for determining the optimal number of clusters, utilizing the elbow method and dendrograms.

1. Part 4 Clustering
Dr. Jyoti Yadav

2. Introduction to Clustering
• Clustering is similar to classification, but the basis is different.
• In Clustering you don’t know what you are looking for, and you are trying
to identify some segments or clusters in your data. When you use
clustering algorithms on your dataset, unexpected things can suddenly
pop up like structures, clusters and groupings you would have never
thought of otherwise.
• Clustering Models
K-Means Clustering
Hierarchical Clustering

3. Introduction to Clustering

4. Introduction to Clustering

5. Types of Clustering

6. Partitioning Clustering

7. Density Based Clustering

8. Distribution Model- Based Clustering

9. Hierarchical Clustering

10. Fuzzy Clustering
• Fuzzy clustering is a type of soft method in which a data object
may belong to more than one group or cluster.
• Each dataset has a set of membership coefficients, which depend
on the degree of membership to be in a cluster.
• Fuzzy C-means algorithm is the example of this type of
clustering; it is sometimes also known as the Fuzzy k-means
algorithm.

11. Clustering Algorithms
• K-Means Algorithm
• Mean-Shift Algorithm
• DBSCAN Algorithm
• Expectation-Maximization Clustering using GMM
• Agglomerative Hierarchical Algorithm
• Affinity Propogation

12. Applications of Clustering
• Search Result Grouping
• Customer Segmentation
• Medical Imaging
• Anomaly Detection
• Market Segmentation
• Social Network Analysis
• Recommendation Engines

13. K-Means Algorithm

14. K-means Clustering Algorithm

15. K-Means Algorithm

16. K-Means Algorithm

17. K-Means Algorithm

18. K-Means Algorithm

19. K-Means Algorithm

20. K-Means Algorithm

21. K-Means Algorithm

22. K-Means Algorithm

23. K-Means Algorithm

24. K-Means Algorithm

25. Random Initialization Trap

26. Random Initialization Trap

27. Random Initialization Trap

28. What if we have a bad random initialization?

29. What if we have a bad random initialization?

30. What if we have a bad random initialization?

31. What if we have a bad random initialization?

32. What if we have a bad random initialization?

33. What if we have a bad random initialization?

34. What if we have a bad random initialization?

35. Choosing the right number of clusters

36. Choosing the right number of clusters

37. Choosing the right number of clusters

38. How to select optimal number of clusters?

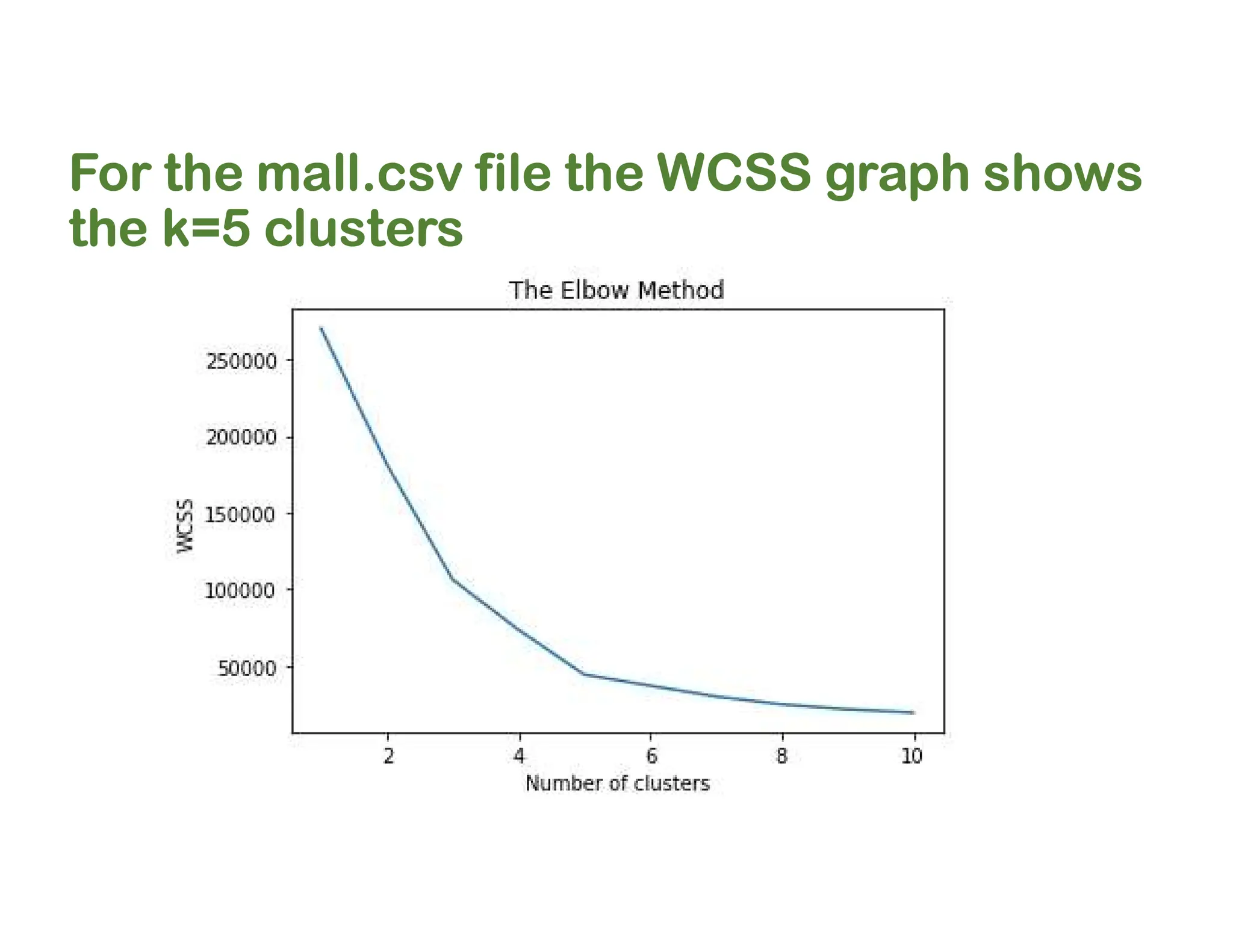
39. WCSS Code
from sklearn.cluster import KMeans
wcss = []
for i in range(1, 11):
kmeans = KMeans(n_clusters = i, init = 'k-means++',
random_state = 42)
kmeans.fit(X)
wcss.append(kmeans.inertia_)
#inertia is a library to compute WCSS
plt.plot(range(1, 11), wcss) # from 1 to 10 clusters
plt.title('The Elbow Method')
plt.xlabel('Number of clusters')
plt.ylabel('WCSS')
plt.show()

40. For the mall.csv file the WCSS graph shows
the k=5 clusters

41. IMP Code for K-means
kmeans = KMeans(n_clusters = 5, init = 'k-means++', random_state = 42)
y_kmeans = kmeans.fit_predict(X)

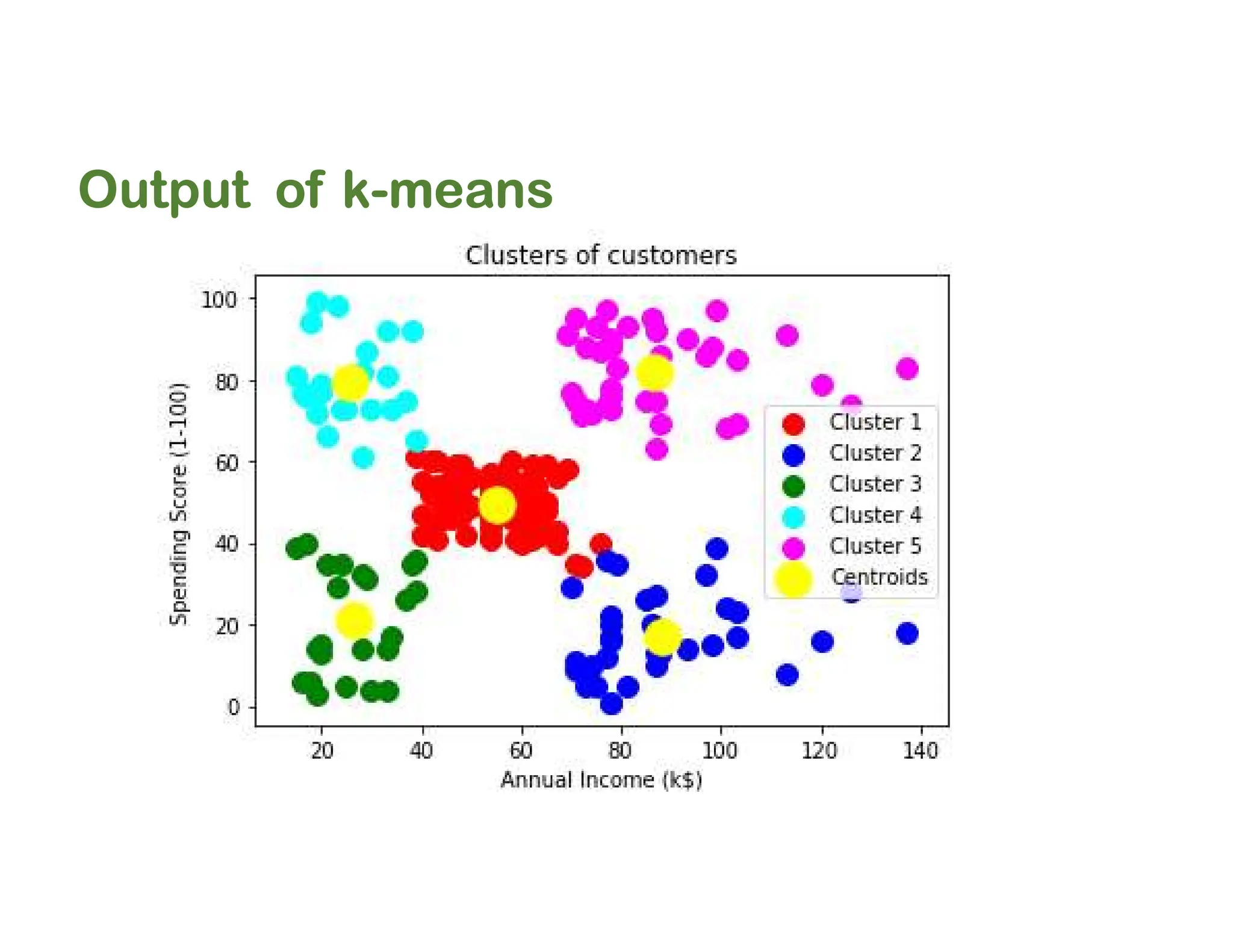
42. IMP Code for K-means
plt.scatter(X[y_kmeans == 0, 0], X[y_kmeans == 0, 1], s = 100, c = 'red', label = 'Careful')
# cluster1, column 1 # cluster 1, column 2
plt.scatter(X[y_kmeans == 1, 0], X[y_kmeans == 1, 1], s = 100, c = 'blue', label = 'Standard')
plt.scatter(X[y_kmeans == 2, 0], X[y_kmeans == 2, 1], s = 100, c = 'green', label = 'Target')
plt.scatter(X[y_kmeans == 3, 0], X[y_kmeans == 3, 1], s = 100, c = 'cyan', label = 'Careless')
plt.scatter(X[y_kmeans == 4, 0], X[y_kmeans == 4, 1], s = 100, c = 'magenta', label =
'Sensible')
plt.scatter(kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], s = 300, c =
'yellow', label = 'Centroids')
plt.title('Clusters of Clients')
plt.xlabel('Annual Income (k$)')
plt.ylabel('Spending Score (1-100)')
plt.legend()
plt.show()

43. Output of k-means

44. Hierarchical Clustering

45. 2 Types of Hierarchical Clustering
•Agglomerative
•Divisive

46. Agglomerative Clustering

47. Distance between Cluster

48. Distance between Cluster

49. Distance between Cluster

50. Distance between Cluster

51. Distance between Cluster

52. Agglomerative Hierarchical Cluster

59. Hierarchical Clustering using a Dendrogram

60. Hierarchical Clustering using a Dendrogram

61. Hierarchical Clustering using a Dendrogram

62. Hierarchical Clustering using a Dendrogram

63. Hierarchical Clustering using a Dendrogram

64. Hierarchical Clustering using a Dendrogram

65. Using Dendrogram to form 2 clusters

66. Using Dendrogram to form 4 clusters

67. Using Dendrogram to form 6 clusters

68. How to find #optimal clusters?

69. How many clusters can be formed from this Dendrogram?

70. #optimal clusters = 3

71. Find the number of Clusters from the Dendrogram

72. Find the number of Clusters from the Dendrogram

73. Using the dendrogram to find the optimal number of clusters
import scipy.cluster.hierarchy as sch
dendrogram = sch.dendrogram(sch.linkage(X, method =
'ward'))
plt.title('Dendrogram')
plt.xlabel('Customers')
plt.ylabel('Euclidean distances')
plt.show()

74. OutputDendrogram

75. Fitting Hierarchical Clustering to the dataset
from sklearn.cluster import AgglomerativeClustering
hc = AgglomerativeClustering(n_clusters = 5, affinity = 'euclidean', linkage = 'ward')
y_hc = hc.fit_predict(X)

76. Output of Hierarchical Clustering