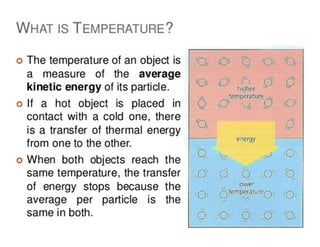
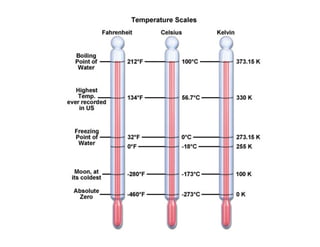
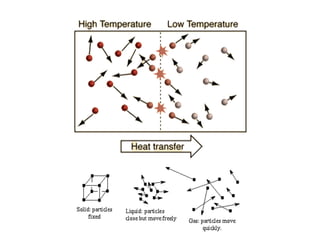
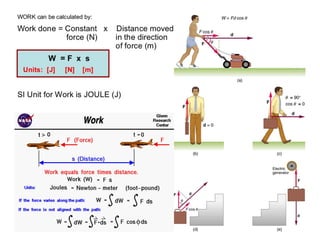
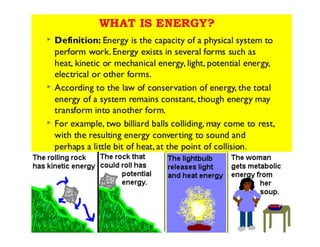
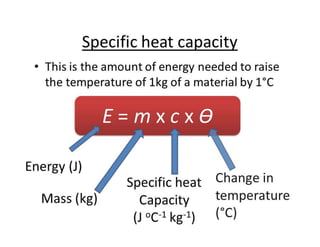
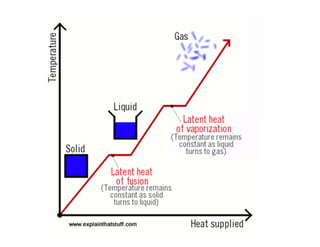
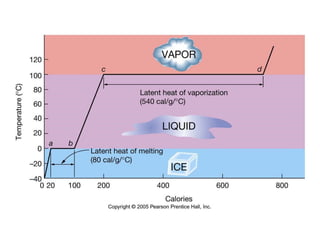
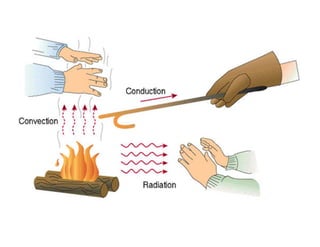
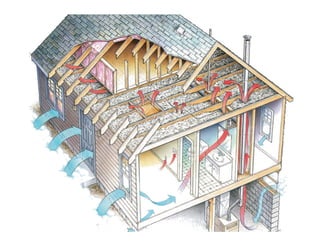
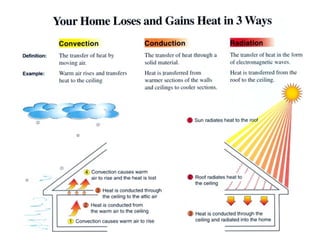
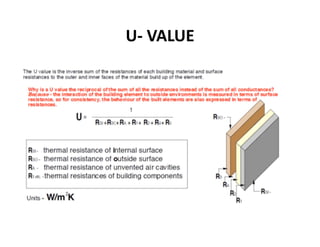
This document provides an in-depth overview of the principles of thermal design and climatology, including essential thermal quantities such as heat, specific heat, latent heat, heat flow, and resistance in materials. It discusses how these concepts influence building design, energy efficiency, and the thermal performance of building materials, particularly focusing on the U-value and its importance in thermal insulation. Through annotations and equations, the document emphasizes the calculations involved in evaluating heat transfer and resistance in the context of building construction.

1. PRINCIPLES OF THERMAL
DESIGN
CLIMATOLOGY,
MBS SPA 2016
Assistant Prof. Rohit Kumar

2. CONTENTS
• The focus is on the understanding of thermal
quanitites like
– Heat,
– specific heat,
– latent heat,
– Heat flow rate,
– Conductance (& resistance),
– Transmittance,
– Sol air temperature,
– Solar gain factor.

3. TEMPERATURE
• Outward appearance of the thermal state of
the body‐ A symptom rather than a physical
quantity. (Unit: degC or degree Celsius)
• Degree of hotness of a body.
– If day time temperature: 36 degC
Night time temp. is 12 degC
Diurnal range is 24 degC

6. HEAT
• A form of energy, appearing as molecular
movement in substances or as ‘radiant heat’, a
certain wavelength band of electromagnetic
radiation in space (700 to 10,000nm).
• Unit: Energy : Joules (J)
– Length: metre (m)
– Mass: kilogramme (kg)
– Time: second (s)
– Speed: m/s
– Acceleration: m/sq.s

8. HEAT
• Force: A push or a pull upon an object resulting
from the object’s interaction with another object.
– Acceleration caused in unit mass of body.
– Unit: kg m/sq.s or Newton
• Work: If unit force acting over unit mass of a
body moves it over unit length.
– Unit: kg sq.m/sq.s or Joule
• Energy: Ability to do work/Potential to carry out
work.
– Property of objects which can be transferred to other
objects or converted to different forms but cannot be
destroyed
– Unit: kg sq.m/sq.s or Joule

12. SPECIFIC HEAT
• Specific heat of a substance is the amount of
heat energy necessary to cause unit
temperature increase of a unit mass of the
substance.
• Higher the specific heat of a substance, the
more heat it will absorb for a given increase in
temperature.
• Water has the highest specific of all common
substances at 4187 J/kg degC.
• Thermal capacity is the product of its mass
and specific heat of its material.

15. LATENT HEAT
• Latent heat of a substance is the amount of
heat energy absorbed by unit mass of the
substance at change of state (from solid to
liquid to gaseous) without any change in
temperature.
• For water, latent heat is:
– Of fusion (0 deg ice to 0 deg water) 335 KJ/kg
– Of vaporization at 100 deg 2261 KJ/kg
– Of evaporation at around 20 deg 2400 KJ/kg

18. HEAT FLOW
• Heat energy tends to distribute itself evenly
until a perfectly diffused uniform thermal field
is achieved.
• It tends to flow from high temperature to
lower temperature in the following ways:
– Conduction
– Convection
– Radiation
• The motive force is the temperature
difference between the two zones or areas
considered.

22. HEAT FLOW RATE
• Rate of heat flow is measured in Watts.
• Power is the ability to do work in unit time. It is
the rate of energy expenditure
• Unit is J/s or Watt
– 1 hp (metric) = 735.5 W
– 1 Btu/h = 0.293 W
– 1 ton of regfrigeration = 3516 W
• A ton of refrigeration is the cooling power of 1
ton (American ‘short’ ton of 2000 lb) of ice
melting in 24 hours.
– 1 ton= (2000 x 144)/24=12000 Btu/h = 12000 x 0.293
W = 3516 W

23. UNITS
• Length: m
• Time: s
• Mass: kg
• Speed: m/s
• Acceleration: m/sq.s
• Force: kg m/sq.s (Newton)
• Work/Energy : kg sq.m/sq.s (Joule)
• Power: kg sq.m/cu.s: J/s : (Watt)
• Specific/Latent heat: J/Kg degC
• Conductivity: Watt/m degC
• Conductance: Watt/ sq.m degC

24. • Conductivity= k‐value
• Resistivity= 1/k
• Conductance= C
• Resistance= R=1/C
• R=b/k (Where b is thickness of the material
and 1/k is resistivity)
BRIEF

25. CONDUCTIVITY
• Heat flow in conduction takes place through
bodies in direct contact, the molecular
movement constituting the flow of heat.
• The rate at which such molecular movements
spreads varies with different materials and is
described as a property of materials called
thermal conductivity (k‐value)
• Thermal conductivity (or 'k‐value') is defined as
the rate of heat flow through unit area of unit
thickness of the material, when there is a unit
temperature difference between the two sides.

26. CONDUCTIVITY & RESISTIVITY
• The unit of measurement is W/m degC.
• Its value varies between 0∙03 W/m degC for
insulating materials and up to 400 W/m degC
for metals.
• The lower the conductivity, the better
insulator a material is.
• Resistivity is the reciprocal of this quantity (1
/k) measured in units of: m degC/W.
• Better insulators will have higher resistivity
values.

27. CONDUCTANCE & RESISTANCE
Whilst conductivity and resistivity are properties
of a material, the corresponding properties of a
body of a given thickness are described as
conductance (C), or its reciprocal resistance (R).
C = 1/R
Conductance is the heat flow rate through a unit
area of the body when the temperature
difference between the two surfaces is 1 degC.
The unit of measurement is W/m² degC.
Resistance of a body is the product of its thickness
(b) and the resistivity of its material:
R = b x 1/ k = b/k
It is measured in m² degC/W.

28. MULTILAYER BODY
• The resistance of a multi layer body of
different materials will be the sum of
resistances of individual layers.
• The conductance (C) can be found by finding
its total resistance (R) and taking its reciprocal:
• C=1/R
Note that the
conductances are
not additive, only
the resistances.

29. SURFACE CONDUCTANCE
• Along with the body, the surface of a material
offers a resistance as well, where a thin film of
air separates the body from the surrounding
air: Surface or thin film resistance.
• Surface conductance is taken to be ‘f’, so
surface resistance will be taken as 1/f.
• It includes convective and radiant components
of the heat exchange at surfaces.

30. OVERALL AIR TO AIR RESISTANCE
• If the heat flow from air to one side on one
side, through the body, to air on the other
side is considered, both surface resistances
must be taken into account.
• The overall air‐to‐air resistance is taken to be
sum of the body’s resistance and the surface
resistance (s) , i.e. te internal surface
resistance and te external surface resistance.

31. OVERALL AIR TO AIR RESISTANCE

32. CAVITIES
If an air space or cavity is enclosed within a
body, through which the heat transfer is
considered, this will offer another barrier to
the passage of heat.
It is measured as the cavity resistance (Rc) which
can be added to the other resistances
described above.

33. CONVECTION
In convection, heat is transferred by the bodily movement
of a carrying medium, usually a gas or a liquid.
The rate of heat transfer in convection depends on three
factors:
 temperature difference (difference in temperature of
the medium at the warmer and cooler points)
 the rate of movement of the carrying medium in terms
of kg/s or m3/s
 the specific heat of the carrying medium in J/kg degC or
J/m3 degC
These quantities will be used in ventilation heat loss or
cooling calculations.

34. In radiation heat transfer, the rate of heat flow depends on the
temperatures of the emitting and receiving surfaces and on
certain qualities of these surfaces: the emittance and
absorbance.
Radiation received by a surface can be partly absorbed and partly
reflected: the proportion of these two components is expressed
by the coefficients absorbance (a) and reflectance (r).
The sum of these two coefficients is always one: a + r = 1
Light coloured, smooth and shiny surfaces tend to have a higher
reflectance.
For the perfect reflective theoretical white surface: r = 1, a = O.
The perfect absorber, the theoretical 'black body', would have the
coefficients: r = 0, a = 1.
RADIATION

35. • U VALUE
• SOL AIR TEMPERATURE
• SOLAR GAIN FACTOR

36. TRANSMITTANCE/ U value
• The reciprocal of air‐to‐air resistance is the air
to air transmittance or U‐value.
• U=1/R
• This is the quantity most often used in
building heat loss and heat gain problems, as
its use greatly signifies the calculations.
• U value of common construction materials are
provided in appendix 5.4. (Koenigsberger)

37. U‐ VALUE
• A U value is a measure of heat loss in a
building element such as a wall, floor or roof.
• It can also be referred to as an ‘overall heat
transfer co‐efficient’ and measures how well
parts of a building transfer heat.
• This means that the higher the U value the
worse the thermal performance of the
building envelope. (Less insulation)

38. U‐ VALUE
• A low U value usually indicates high levels of
insulation.
• They are useful as it is a way of predicting the
composite behaviour of an entire building
element rather than relying on the properties
of individual materials.
• U values are important because they form the
basis of any energy or carbon reduction
standard.

39. U‐ VALUE
• The U value is defined as being reciprocal of all the
resistances of the materials found in the building element.
• The resistance of a building material is derived by the
following formula:
R = (1/k) x d
where k is the conductivity of the building material and d is the
material thickness.
• The formula for the calculation of a U value is
U(element) = 1 / (Rso + Rsi + R1 + R2 ...)
where Rso is the fixed external resistance
where Rsi is the fixed internal resistance
and R1… is the sum of all the resistances of the building
materials in the constructional element.

40. U‐ VALUE

41. U‐ VALUE EXERCISE
• Compare the U‐value of a south facing
normal brick wall and a concrete wall of
thickness 230mm each.
• (Refer to Appendix 5.1 and 5.2 of
Koenisberger for the supporting data)

42. • Conductivity= k‐value
• Resistivity= 1/k
• Conductance= C
• Resistance= R=1/C
• R=b/k (Where b is thickness of the material
and 1/k is resistivity)
• Surface resistance= 1/fi, 1/fo
• Overall air to air resistance= R`=R+1/fi+1/fo
• Transmittance/U‐Value= U = 1/R`
BRIEF

43. SOL‐AIR TEMPERATURE
• For building design purposes, it is useful to
combine the heating effect of radiation
incident on a building with the effect of warm
air: sol‐air temperature concept. (Effect of
Convection +radiation on building)
• A temperature value is found which would
create the same thermal effect as the incident
radiation in question and this value is added
to air temperature.

44. SOL‐AIR TEMPERATURE

45. SOL‐AIR TEMPERATURE
• In cold climate (heat loss situation), a lesser
surface conductance would help reducing heat
loss.
• In warm climate (heat gain situation), a greater
surface conductance would help in reducing solar
over‐heating.
• The reason being the incident radiation increases
surface temperature far above the air temp. and
some heat is dissipated to out door air
immediately. Greater the s.c, more heat will be
dissipated before it can be conducted away by
wall.

46. SOLAR GAIN FACTOR
• To consider the combined effects of reflective
surfaces and thermal insulation.
• To reduce solar heat gain, a dark, highly
absorptive surface with good insulation may
be just as effective as a more reflective but
less well‐insulated element.

47. SOLAR GAIN FACTOR

48. SOLAR GAIN FACTOR
• The heat flow rate through the construction
due to solar radiation expressed as a fraction
of the incident solar radiation.
• As this value can be related to the increase in
the inner surface temperature, a performance
requirement can be established on the basis
of experience, in terms of this solar gain
factor.
• Value should not exceed 0.04 in warm humid
climate and 0.03 in hot dry part of composite
climate when ventilation is reduced.

49. ANNEXURES

50. • Thermal resistance (R) and thermal
conductance (C) of the materials are
reciprocals of one another and can be derived
from thermal conductivity (k) and the
thickness of the materials.
• Thermal conductance
A measure of the ability of a material to transf
er heat per unit time, givenone unit area of th
e material and a temperature gradient throug
h thethickness of the material.

51. k-value – Thermal Conductivity
Thermal conductivity is the time rate of steady state heat flow through a unit area of a homogeneous material induced by a unit temperature
gradient in a direction perpendicular to that unit area, W/m⋅K.
(1)
Where,
L – Thickness of the specimen (m)
T – Temperature (K)
q – Heat flow rate (W/m2)
R-value – Thermal Resistance
Thermal resistance is the temperature difference, at steady state, between two defined surfaces of a material or construction that induces a unit
heat flow rate through a unit area, K⋅m2/W. According to this definition and Equation 1, Equation 2, therefore, can be obtained.
As indicated in Equation 2, the value of the thermal resistance can be determined by dividing the thickness with thermal conductivity of the
specimen.
(2)
C-value – Thermal Conductance
Thermal conductance is the time rate of steady state heat flow through a unit area of a material or construction induced by a unit temperature
difference between the body surfaces, in W/m2⋅K. C-value, hence, is the reciprocal of the R-value and can be expressed as Equation (3).
(3)
Consequently, the value of the thermal conductance can be calculated by dividing the thermal conductivity with the thickness of the specimen.

52. BIBLIOGRAPHY
• Koenigsberger, O. H., Manual of Tropical
Housing and building, Orient Longman private
limited, 1973.