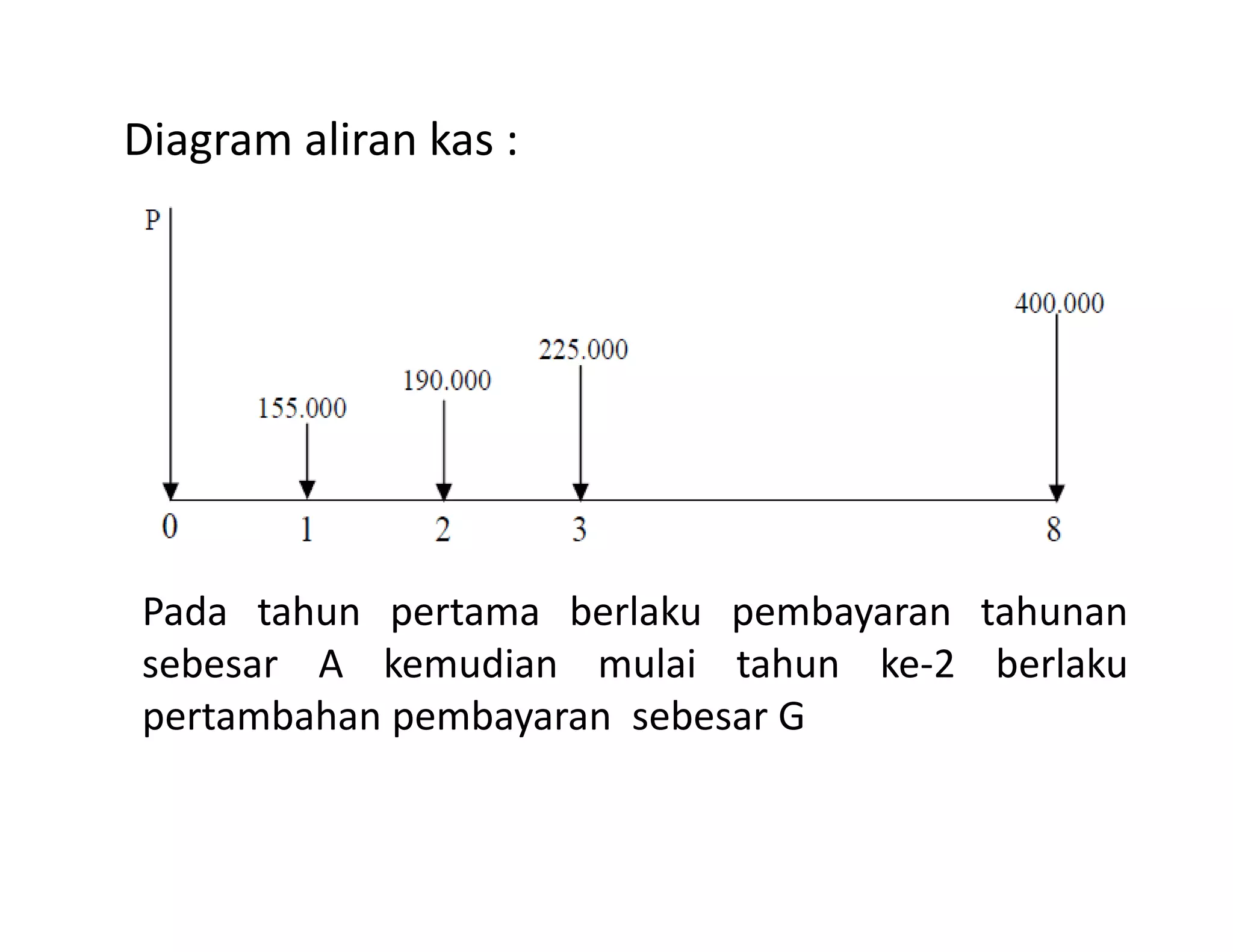
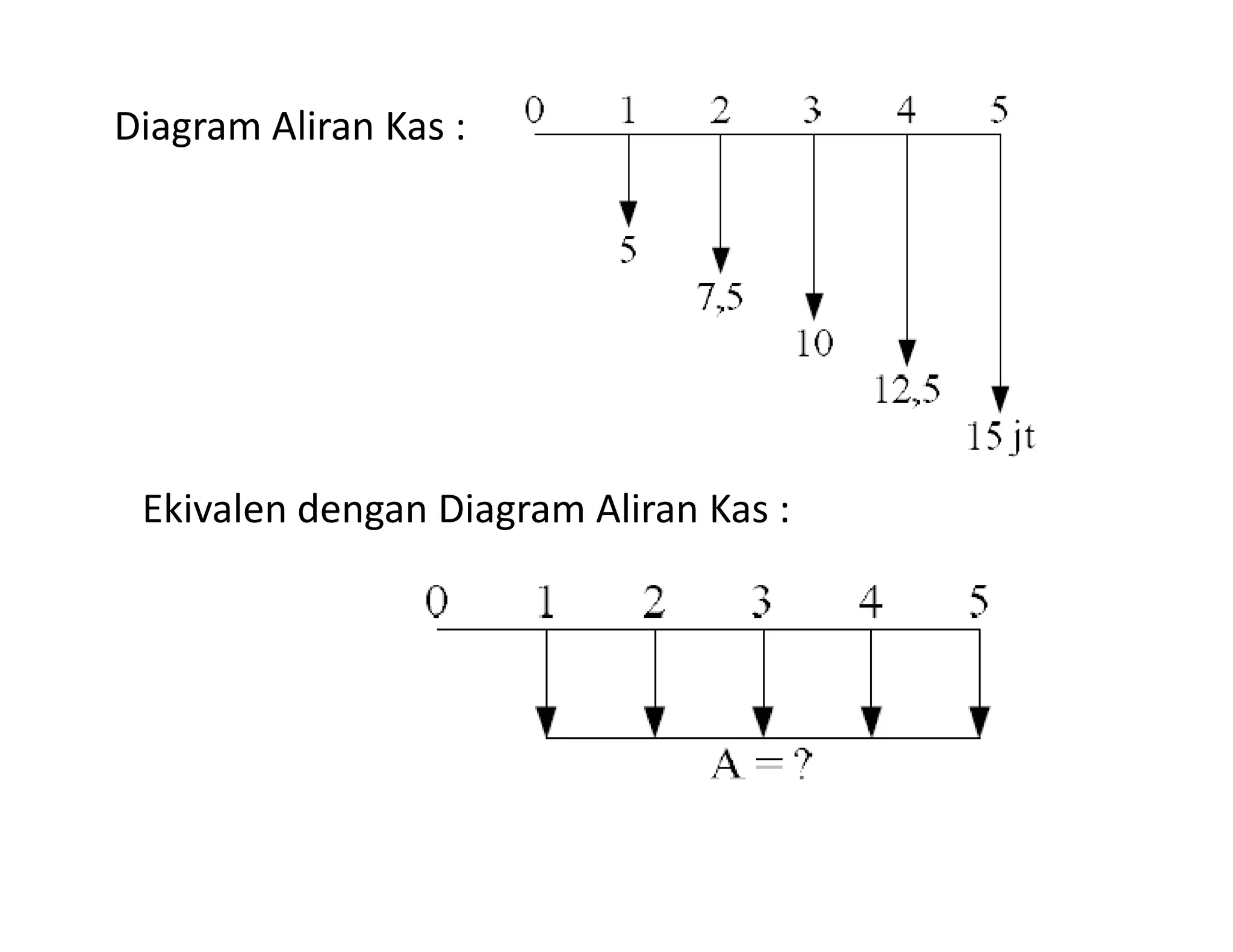
1. Dokumen tersebut membahas tentang gradient uniform atau pembayaran yang teratur dimana besarnya jumlah pembayaran mengalami kenaikan atau penurunan per tahun dengan jumlah yang sama. Metode ini digunakan untuk mengkonversi pembayaran yang tidak merata menjadi pembayaran tahunan yang setara. 2. Diberikan beberapa contoh perhitungan menggunakan metode gradient uniform untuk mengkonversi biaya operasional kendaraan, mesin,

1. Gradient Uniform
Pembayaran Yang Tidak Merata
Univ. Atma Jaya Makassar, Simon Patabang, ST., MT.

2. Definisi
• Gradient Uniform adalah cara pembayaran yang
teratur (seri) dimana besarnya jumlah pembayaran
mengalami kenaikan atau penurunan per tahun
dengan jumlah yang sama.
• Misalnya biaya perawatan yang cenderung naik
setiap tahun adalah :
– Mesin produksi
– Mobil
• Dengan menggunakan pembayaran akhir tahun,
maka jumlah pembayaran selalu mengalami kenaikan
sebesar G dari tahun sebelumnya, spt digambarkan
pada diagram aliran kas .

3. Diagram Aliran Dana
Pada tahun pertama berlaku pembayaran tahunan
sebesar A kemudian mulai tahun ke-2 berlaku
pertambahan pembayaran sebesar G

4. Pembayaran setiap tahun adalah sebagai berikut :
Akhir Tahun ke- Pembayaran
1 0
2 G
3 2G
4 3G4 3G
…. …..
…. …..
( n-1 ) (n-2)G
n (n-1)G

5. • Akumulasi pembayaran pada akhir tahun ke-n adalah
sejumlah F dengan faktor bunga majemuk sebesar :
• Maka besarnya nilai F adalah jumlah dari Faktor
bunga majemuk setiap akhir tahun dikalikan dengan
besarnya kenaikan pembayaran sebesar G.

6. Faktor bunga majemuk dari pembayaran G tiap akhir
tahun yg dimulai pada tahun ke-2 adalah :
Tahun ke- Faktor Bunga Majemuk
2 [(1 + i) - 1 ] / i
3 [(1 + i)² - 1 ] / i3 [(1 + i)² - 1 ] / i
4 [(1 + i)³ - 1 ] / i
…….. …………
n – 1 [(1 + i)ⁿ⁻² - 1 ] / i
n [(1 + i)ⁿ⁻¹ - 1 ] / i

7. Jumlah dari faktor majemuk adalah :

8. Maka :
Jika F adalah nilai pada periode
ke-n dari serangkaian pembaya
ran yg merata, dimana F adalah :

9. 1. Faktor konversi gradien menjadi pembayaran tahunan
yang merata. (Menyatakan hubungan antara A dan G).
A = G(A/G, i %, n)
2. Faktor konversi gradien menjadi nilai sekarang
(Menyatakan hubungan antara P dan G)
P = G (P/G, i %, n)
Gunakan Tabel D30 (A/G) dan D31 (P/G) untuk mencari
faktor konversi gradien untuk i, n, dan G diketahui.

10. Contoh :
1. Biaya pengoperasian dan pemeliharaan suatu mesin
produksi pada akhir tahun pertama adalah Rp.155.000,
dan naik tiap tahun sebesar Rp. 35.000,- selama 7
tahun. Berapakah uang yang harus disediakan sekarang
untuk pengoperasian dan pemeliharaan selama 8 tahun
jika suku bunga 6% tiap tahun.
Penyelesaian :
Diketahui :
A = Rp.155.000, G = Rp. 35.000, n = 8, i= 6%
Ditanyakan : P untuk n = 8

11. Diagram aliran kas :
Pada tahun pertama berlaku pembayaran tahunan
sebesar A kemudian mulai tahun ke-2 berlaku
pertambahan pembayaran sebesar G

12. P = A(P/A,6%,8) + G (P/G,6%,8)
P = 155.000 (P/A, 6 %, 8) + 35.000 (P/G, 6 %, 8)
P = 155.000 (6,210) + 35.000 (19,842) = Rp. 1.657.200,-
Jadi jumlah uang yang diperlukan sekarang adalah Rp.
1.657.200,-1.657.200,-

13. 2. Sebuah kontraktor menyediakan kendaraan
operasional untuk memantau setiap proyek. Jika
biaya operasinal dan pemeliharaan kendaraan dari
tahun pertama sampai tahun kelima, berturut-turut
Rp.5 Juta, Rp.7,5 juta, Rp. 10 juta, Rp.12,5 juta,
Rp.15 juta. Berapakah biaya per tahunnya jika
diketahui tingkat suku bunga 20% per tahun.diketahui tingkat suku bunga 20% per tahun.
Penyelesaian :
Diketahui : A = Rp. 5 juta, G = Rp. 2,5 juta, i= 20%, n = 5
Ditanyakan : A ?

14. Diagram Aliran Kas :
Ekivalen dengan Diagram Aliran Kas :

15. A = A1 + G(A/G,i,n)
A = Rp. 5 juta + Rp. 2,5 juta (A/G, 20,5)
A = Rp. 5 juta + Rp. 2,5 juta (1,6045)
A = Rp. 5 juta + Rp. 4,01125 juta
A = Rp.9,01125 juta/th.
Besarnya pembayaran per tahun adalah :
Rp.9,01125

16. 3. Sebuah mesin giling padi dibeli dengan harga $6000. Diperkirakan
umur mesin adalah 6 tahun tanpa nilai sisa pada kahir umurnya.
Pengeluaran untuk pajak, asuransi, perawatan, dll pada tahun
pertama sebesar $1500, tahun ke-2 $1700, tahun ke-3 $1900 dan
terus naik sebesar $200 tiap tahunnya. Berapa besar biaya
ekivalen tahunan jika tingkat suku bunga yg berlaku 12%.
Penyelesaian :
Diketahui : P= $6000, A = $1500, G=$200, i=12%, n= 6
Ditanyakan : A/tahun?Ditanyakan : A/tahun?
• Ada pengeluaran tahunan yang berhubungan dengan P pada saat
pembelian. (A/P)
• Setelah berjalan 1 tahun, maka ada pengeluaran tahun pertama A
sebesar $1500.
• Pada tahun kedua dst, terjadi kenaikan pembayaran sebesar $200
dari tahun sebelumnya. (A/G)
• Total pengeluaran tahunan adalah (A/P + A + A/G)

17. Diagram Aliran Kas
Pembayaran yg tidak merata diubah
menjadi pembayaran tahunan uniform
ekivalen.
A = (A/P) + A + (A/G)
A= (A/P,i%,n)+ A + G(G/A,i%,n)
A= P(A/P,12%,6)+ A + G(G/A,12%,6)
A= 6000(0,24323) + 1500 + 200(2,172)
A = $1459 + $1500 + $434
A = $3,393

18. 4. PT ABC menyewakan mesin alat berat kepada anda
selama 6 tahun dengan syarat : Pembayaran pertama
$2000 dan uang sewa pada tiap akhir tahun. Uang sewa
tahun pertama sebesar $2400 dan tahun berikutnya
berkurang sebesar $300 dari sebelumnya. Pada akhir
tahun ke-6, mesin dikembalikan ke PT ABC. Jika suku
bunga 8%.
a. Berapa ongkos tahunan ekivalen sewa mesina. Berapa ongkos tahunan ekivalen sewa mesin
b. Berapakah Nilai Sekarang ekivalen sewa mesin
Penyelesaian :
Diketahui : P1 = $2000, A= $2400, G = -$300, i=8%,n=6
Ditanyakan : A?

19. a. Ongkos tahunan ekivalen sewa mesin
A = (P/A) + A + (G/A)
A = P(P/A,8%,6) + A + G(G/A,8%,6)
A = 2000 (0,21632) + 2400 + (-300) (2,28)
A = $2.149
b. Nilai Sekarang ekivalen sewa mesin .
Untuk mendapatkan nilai sekarang, maka dikonversi menjadi (P/A) dan
(P/G)
P = P1 + (P/A) + (P/G)
P = 2.000 + 2000 (4,623) + (-300) (10,5233)
P = 2.000 + 11.095 – 3.157
P = $9.938

20. SekianSekian