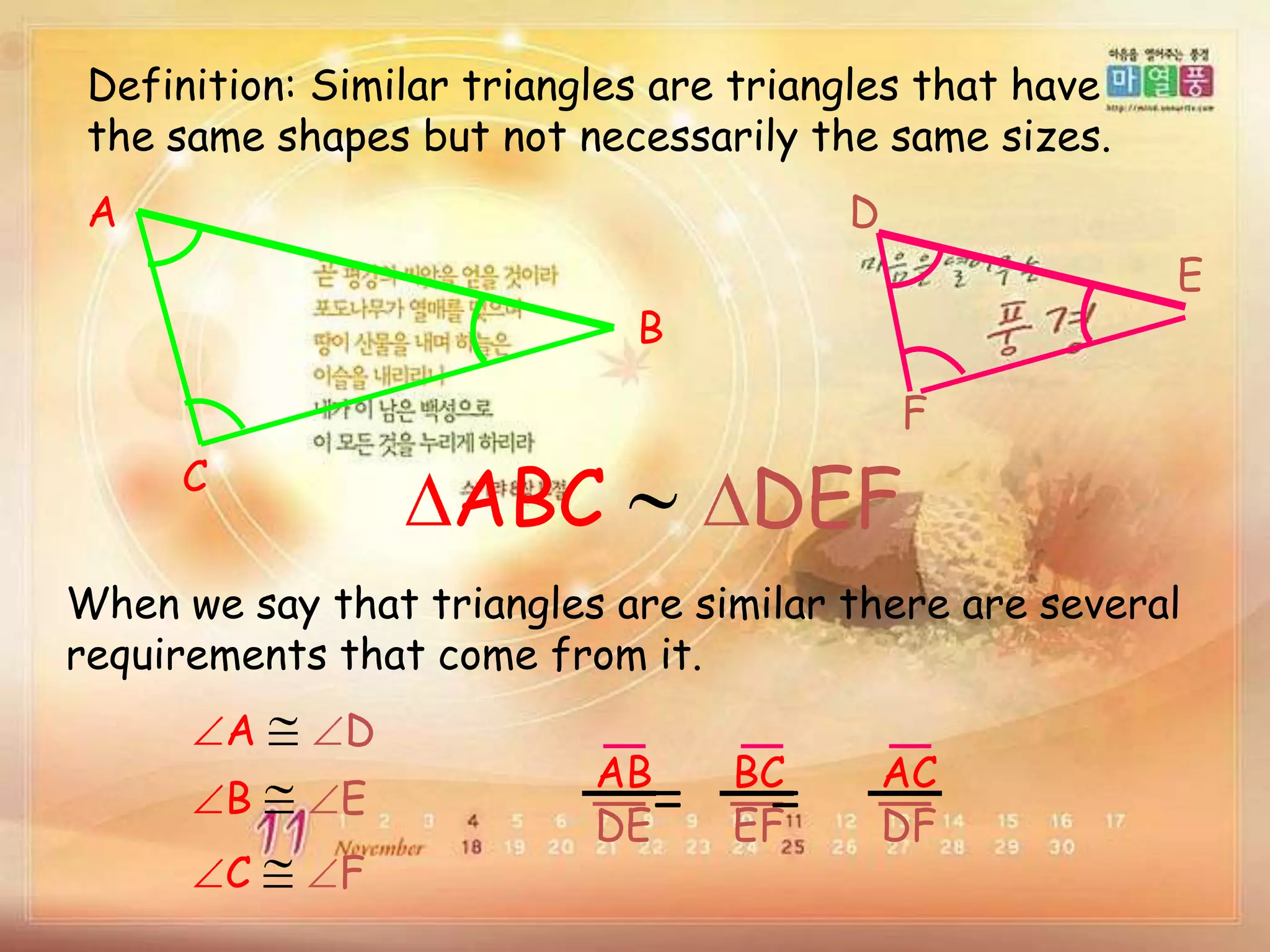
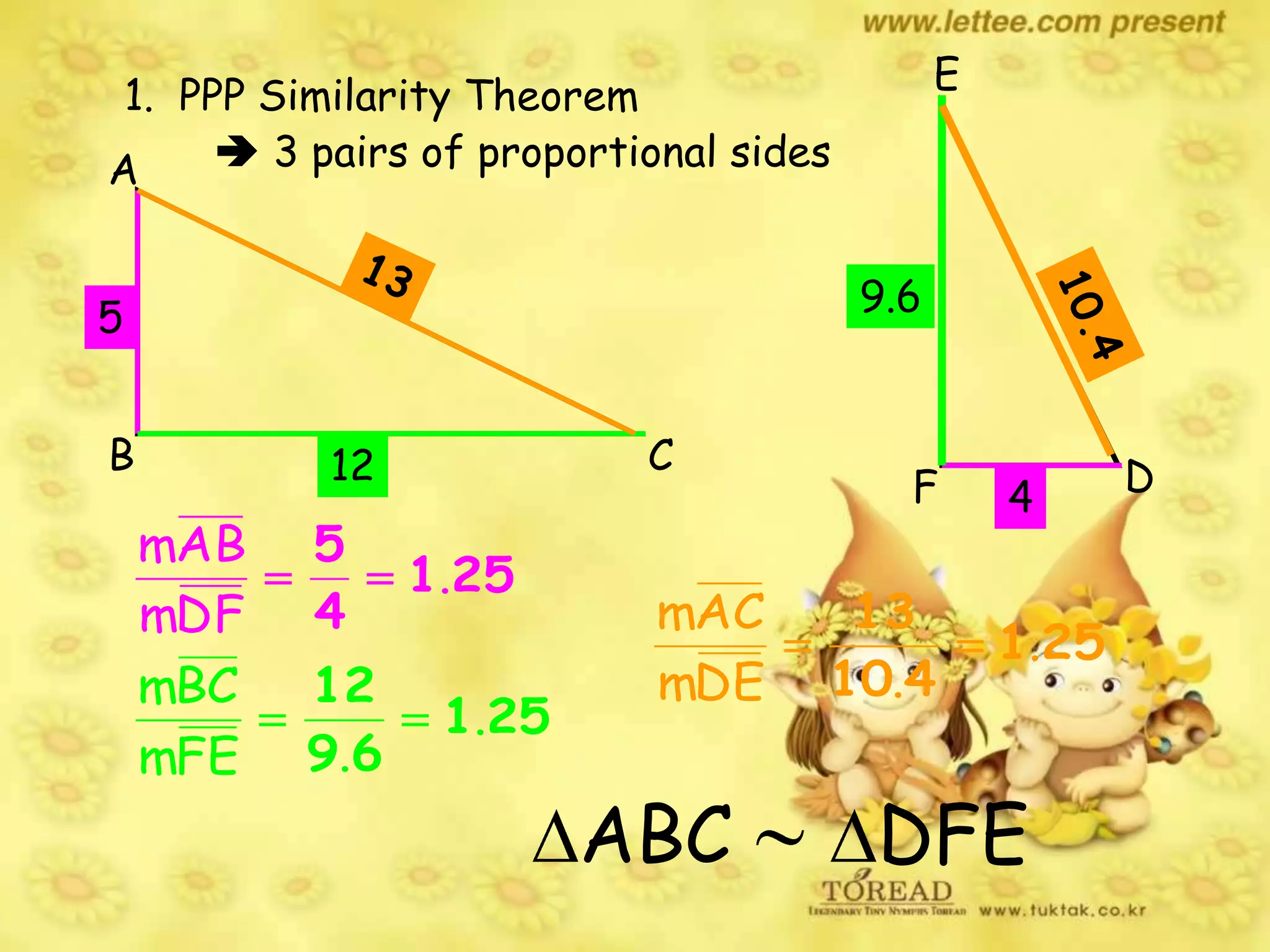
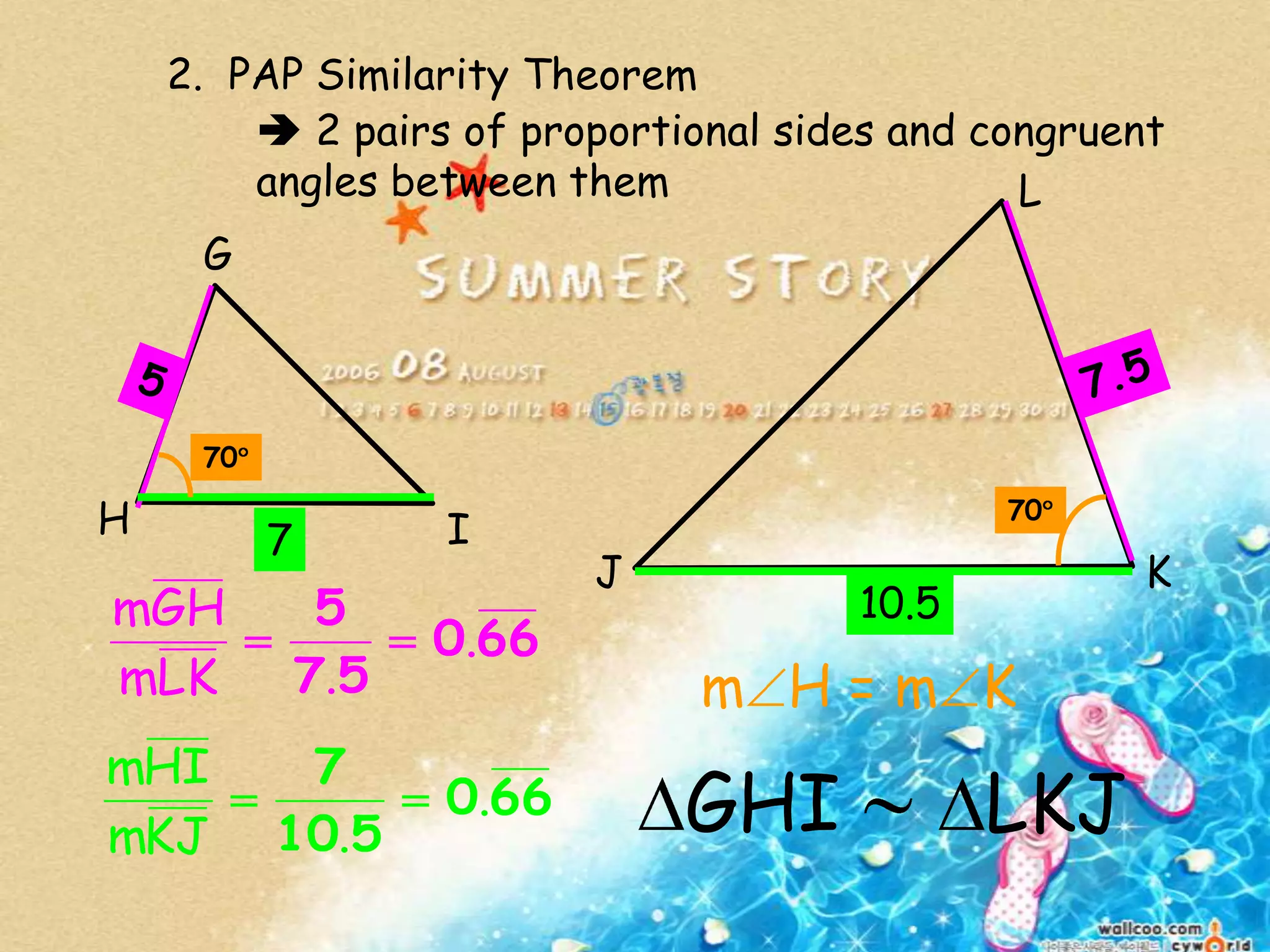
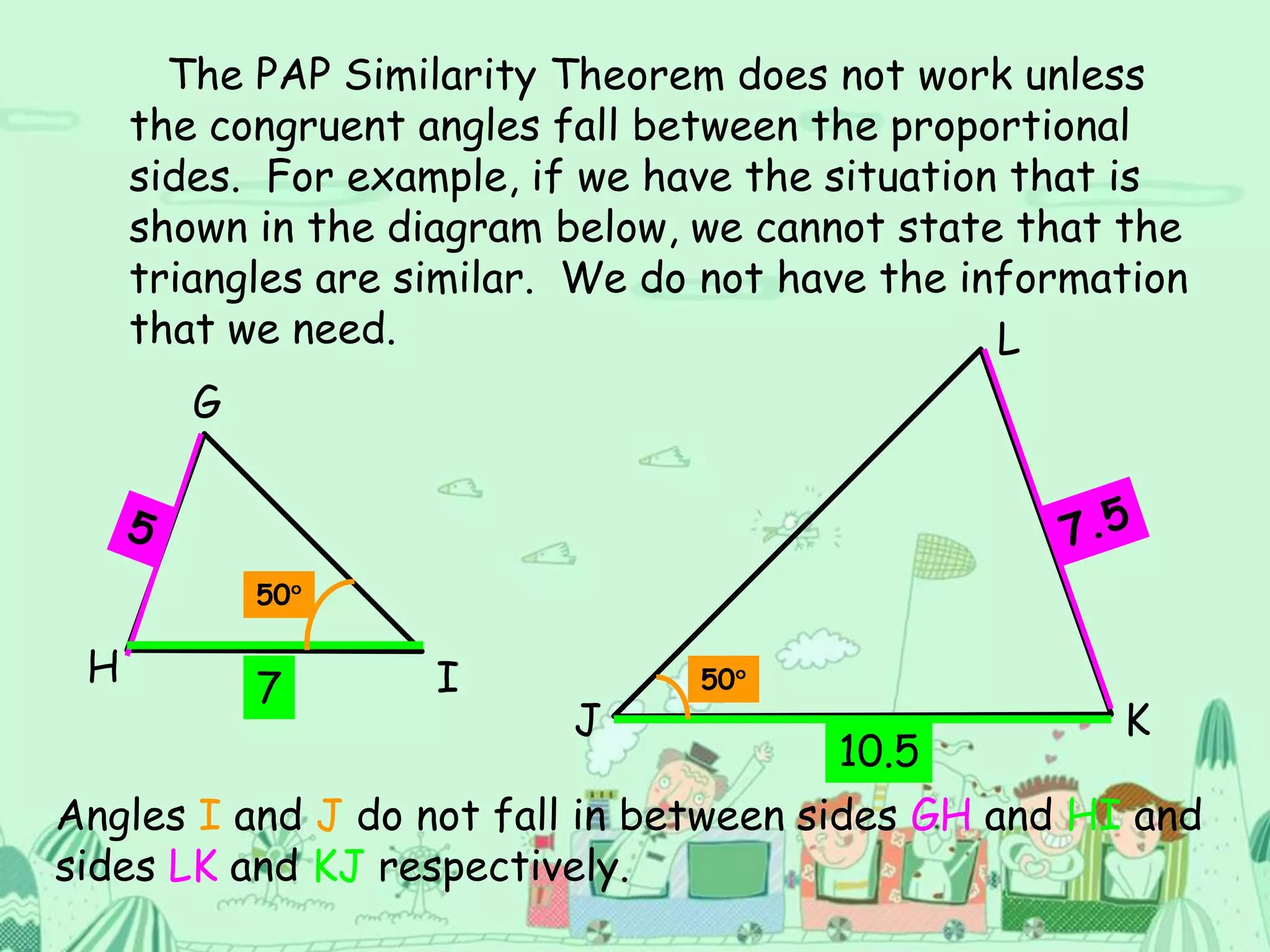
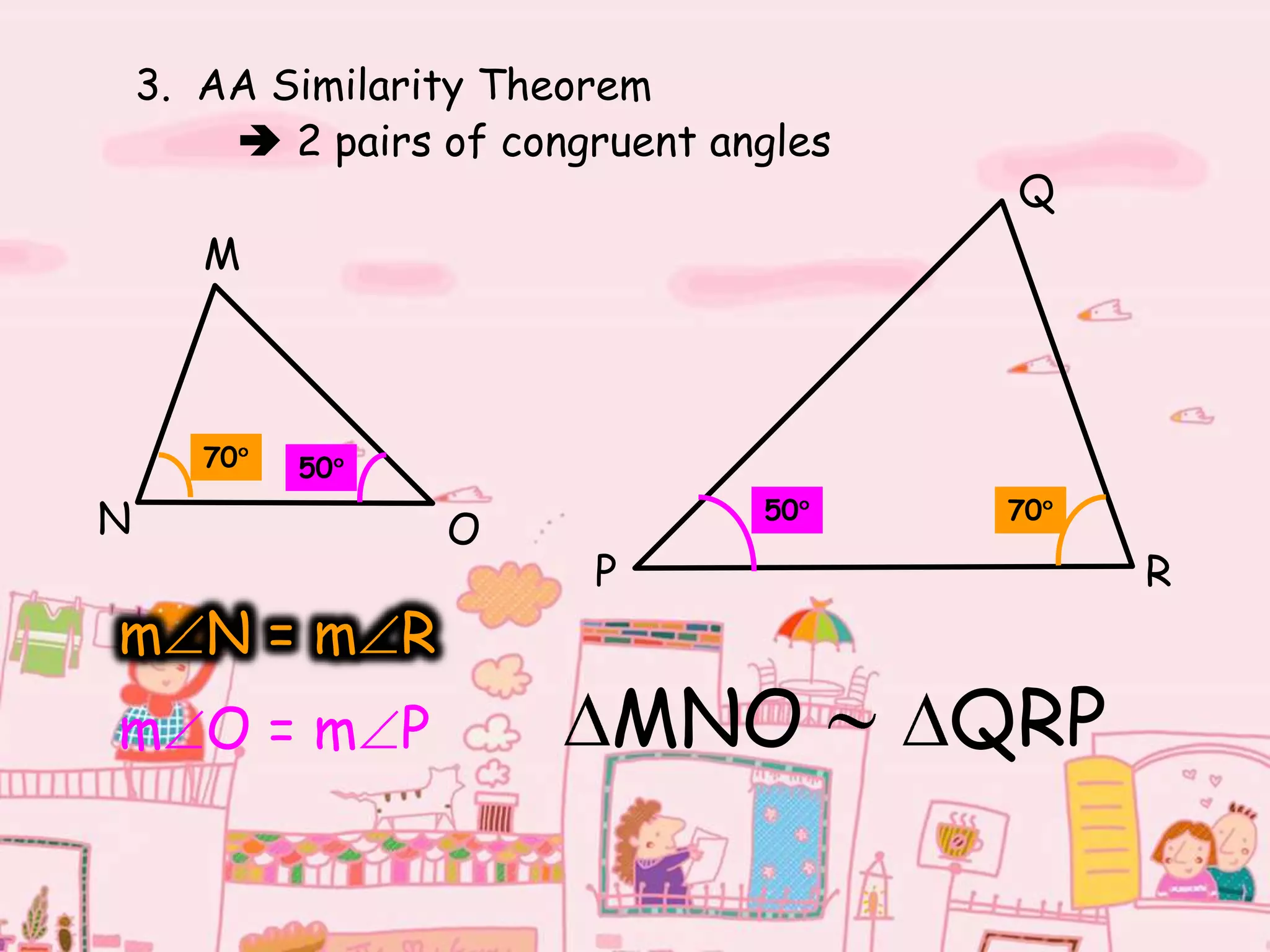
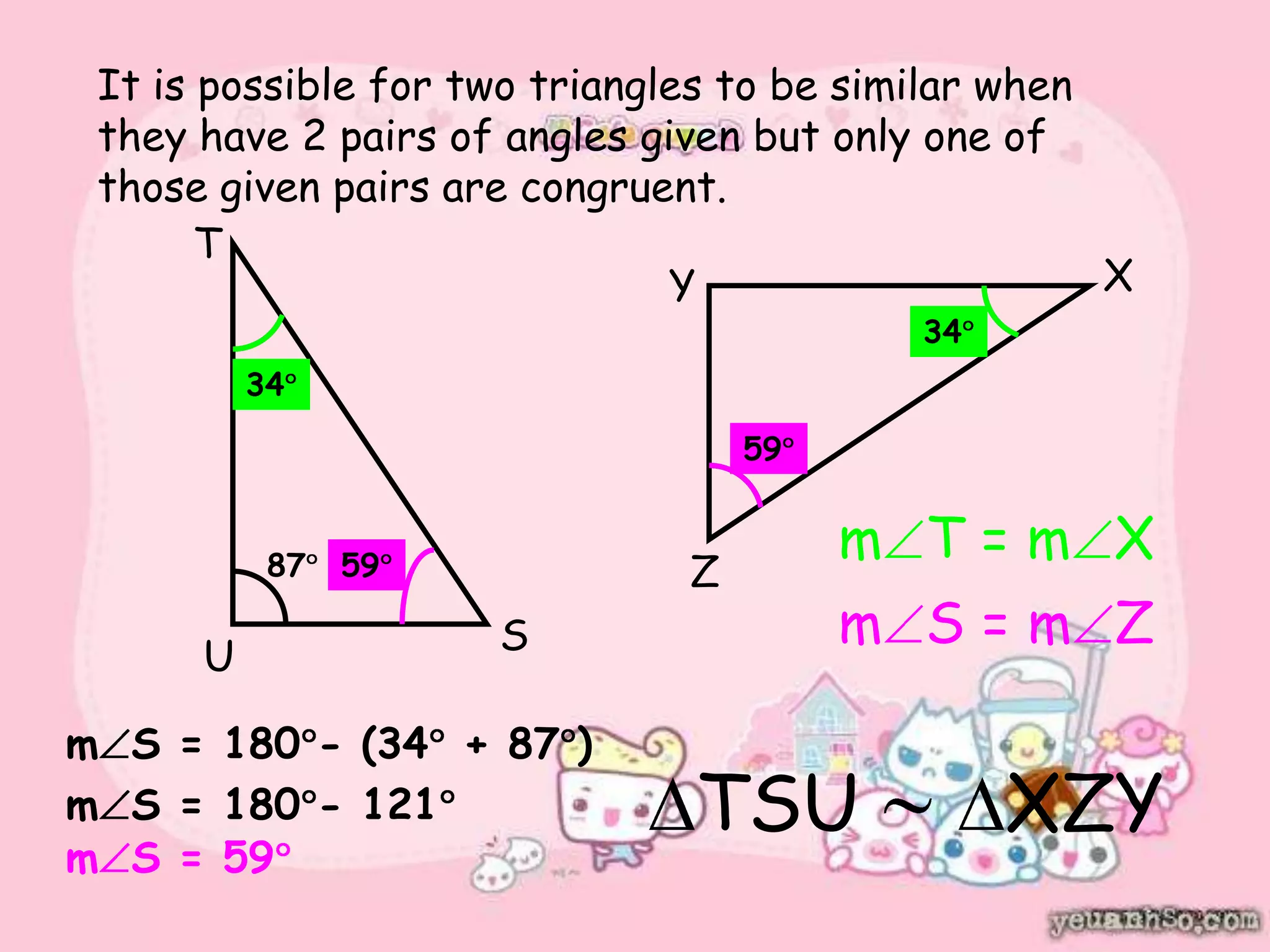
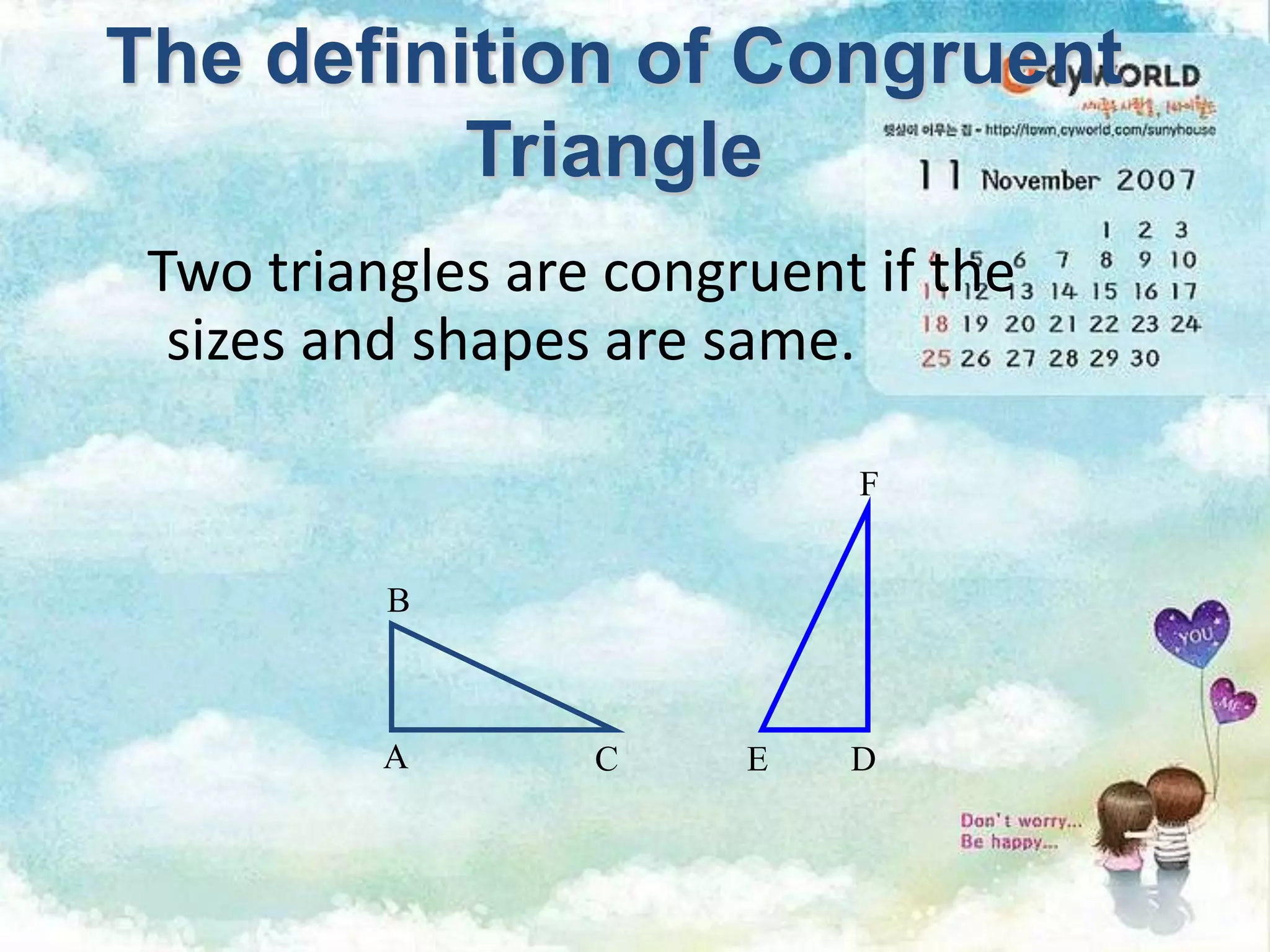
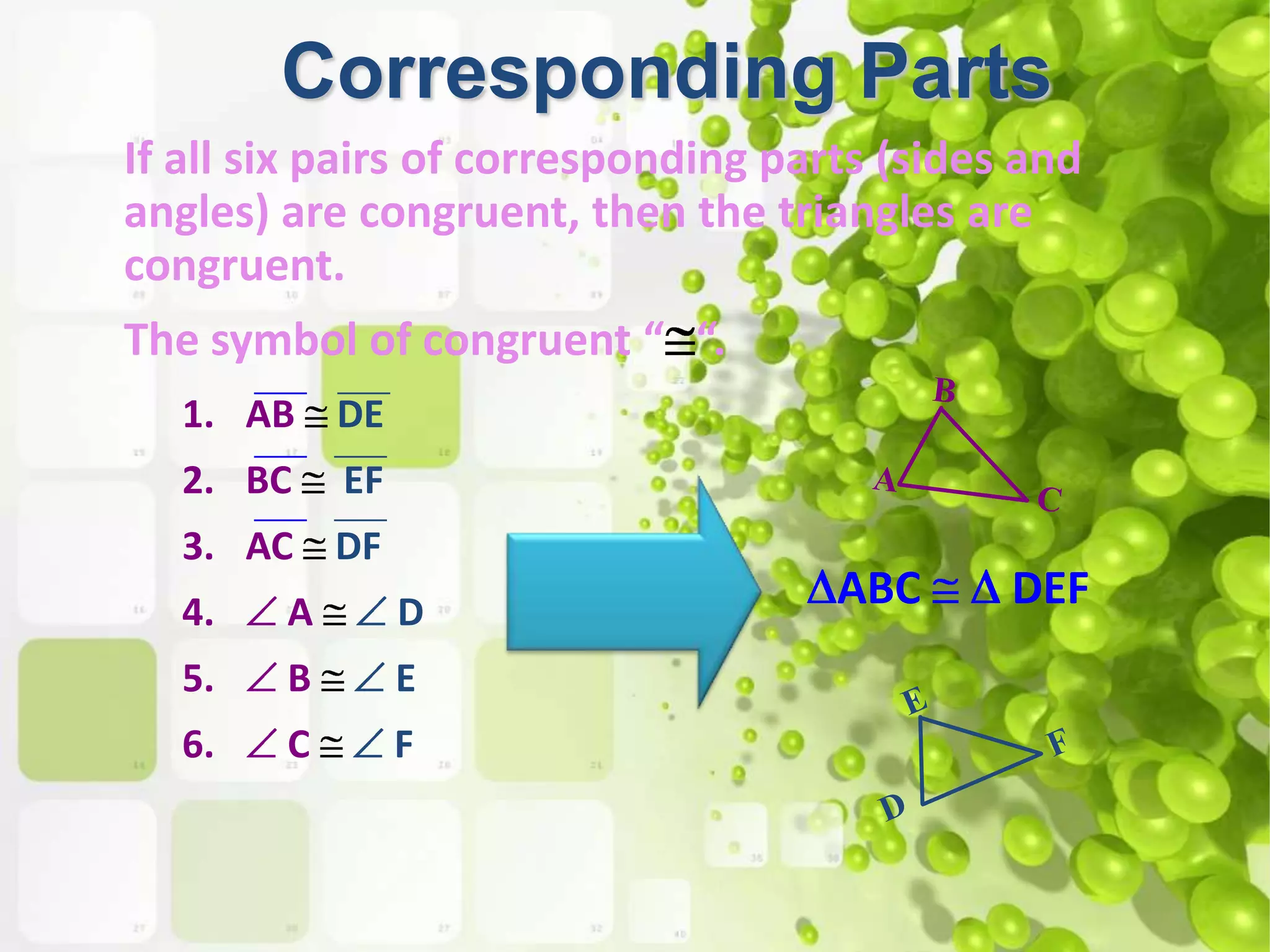
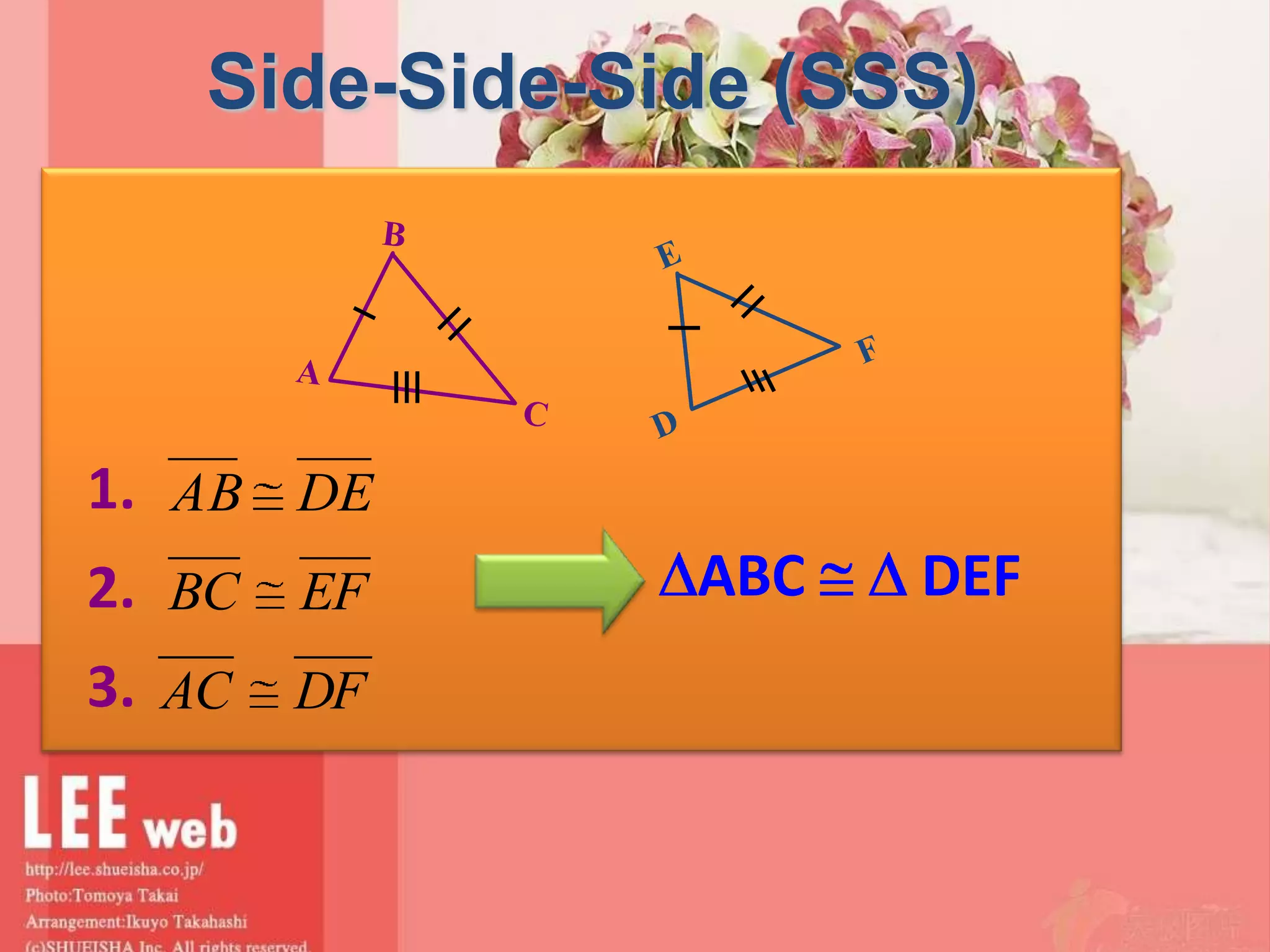
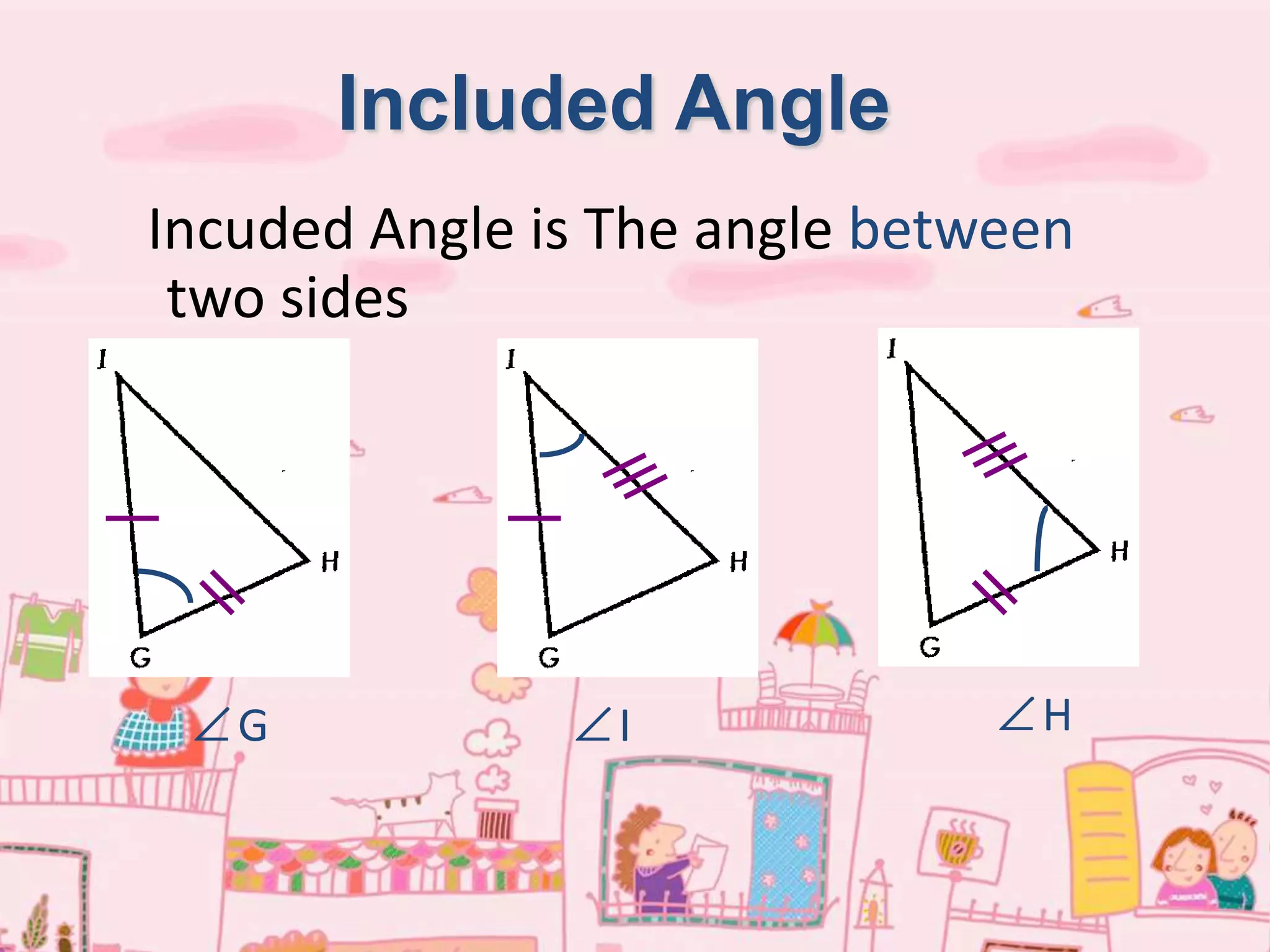
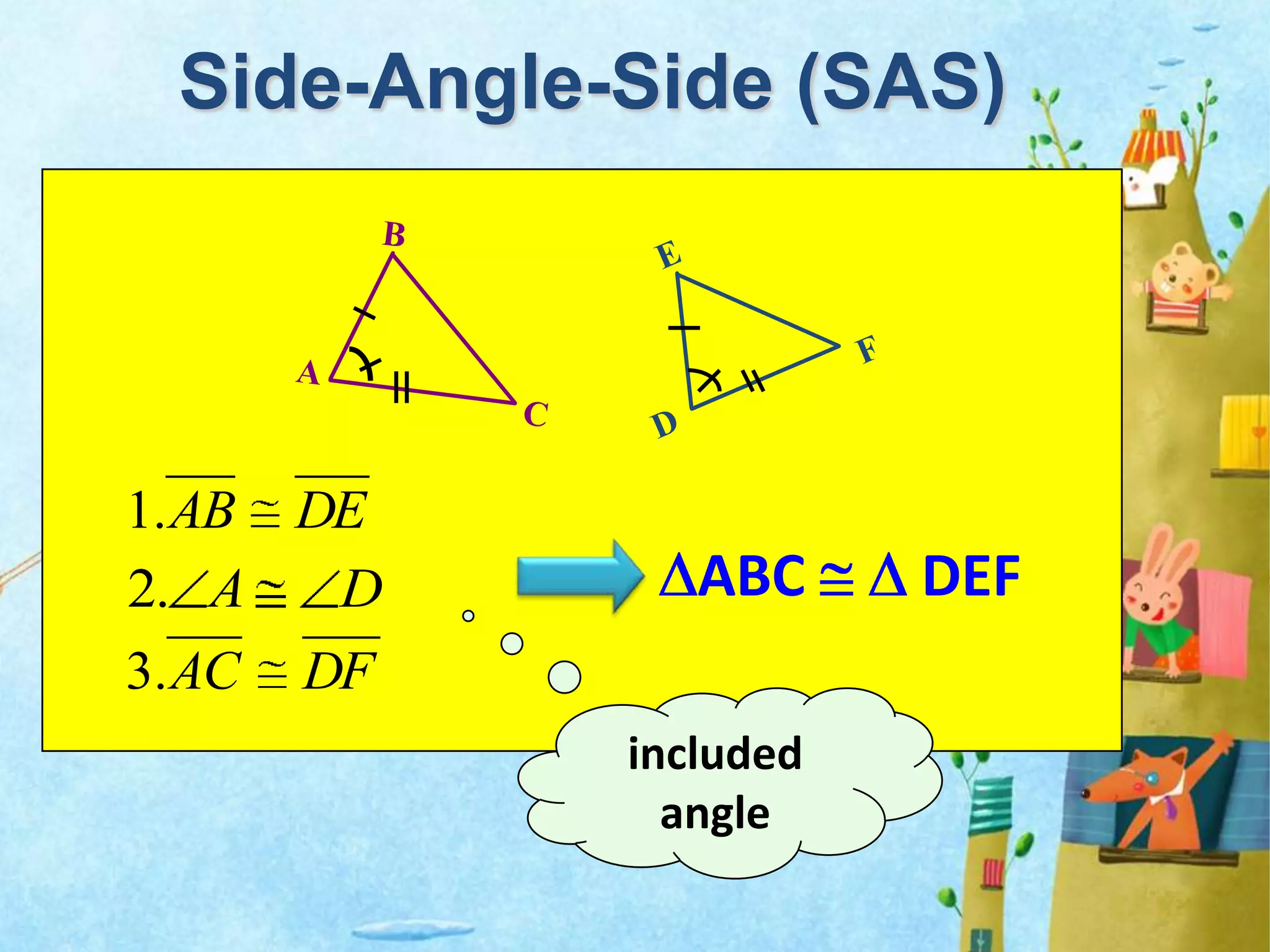
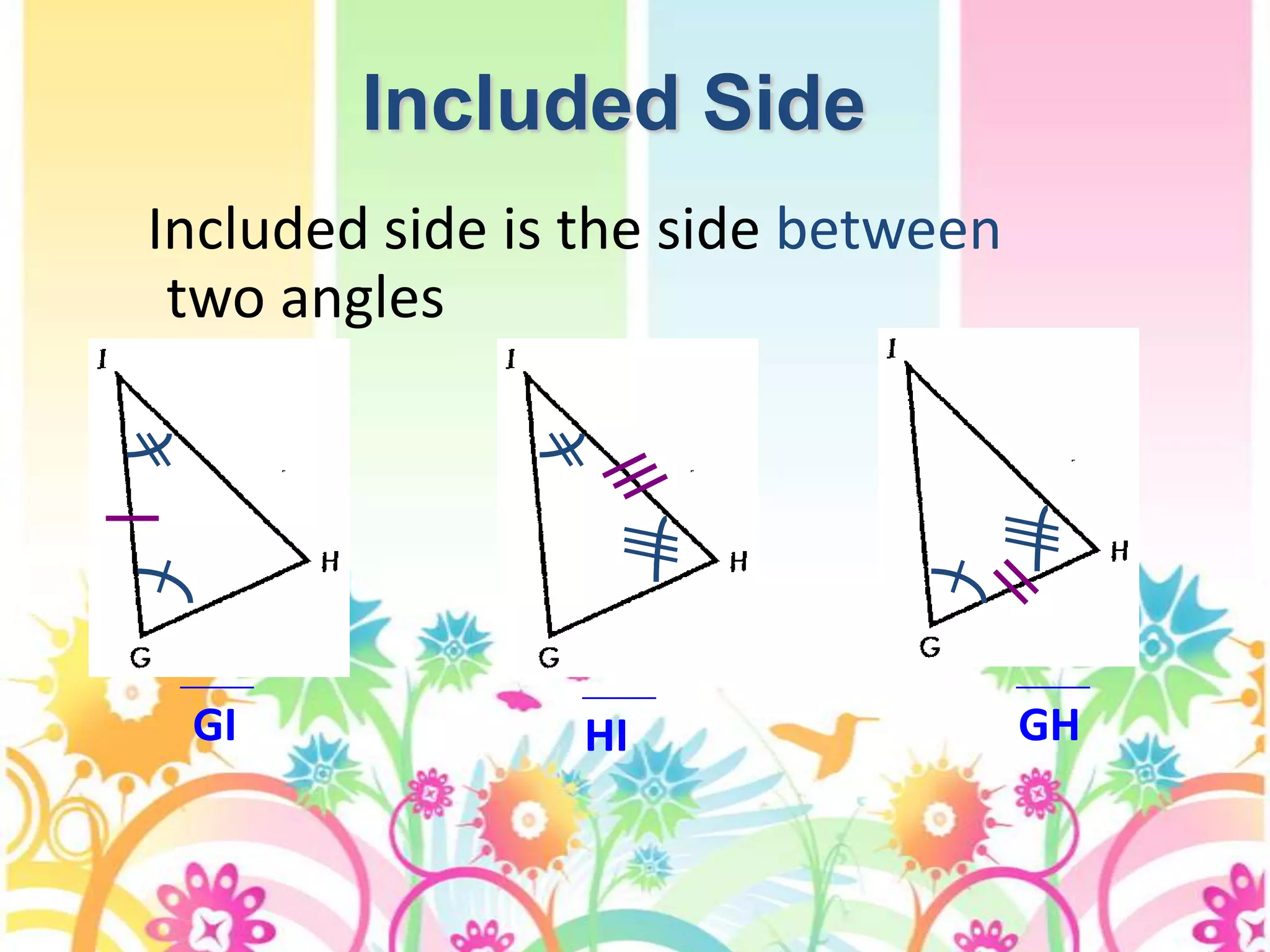
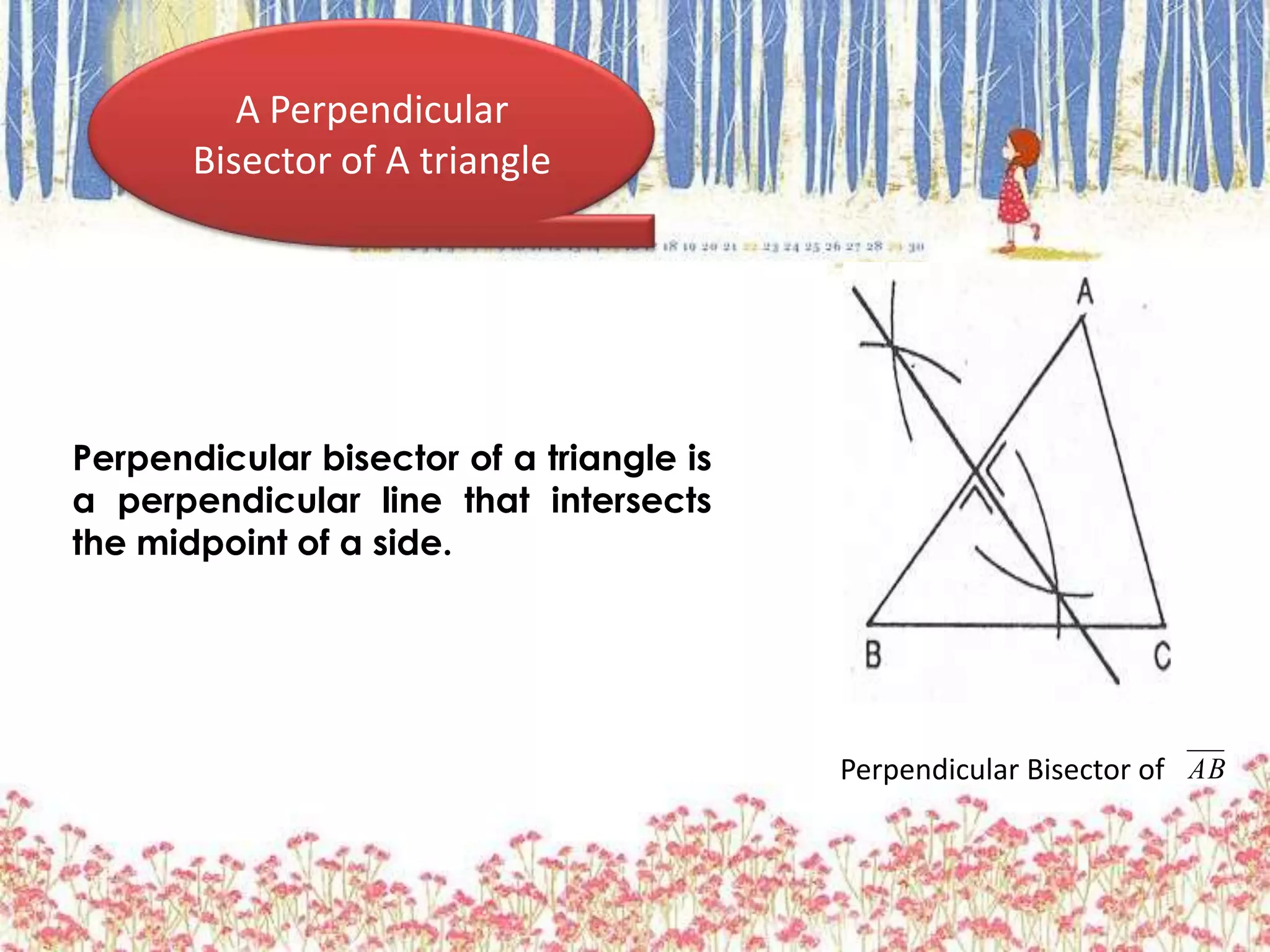
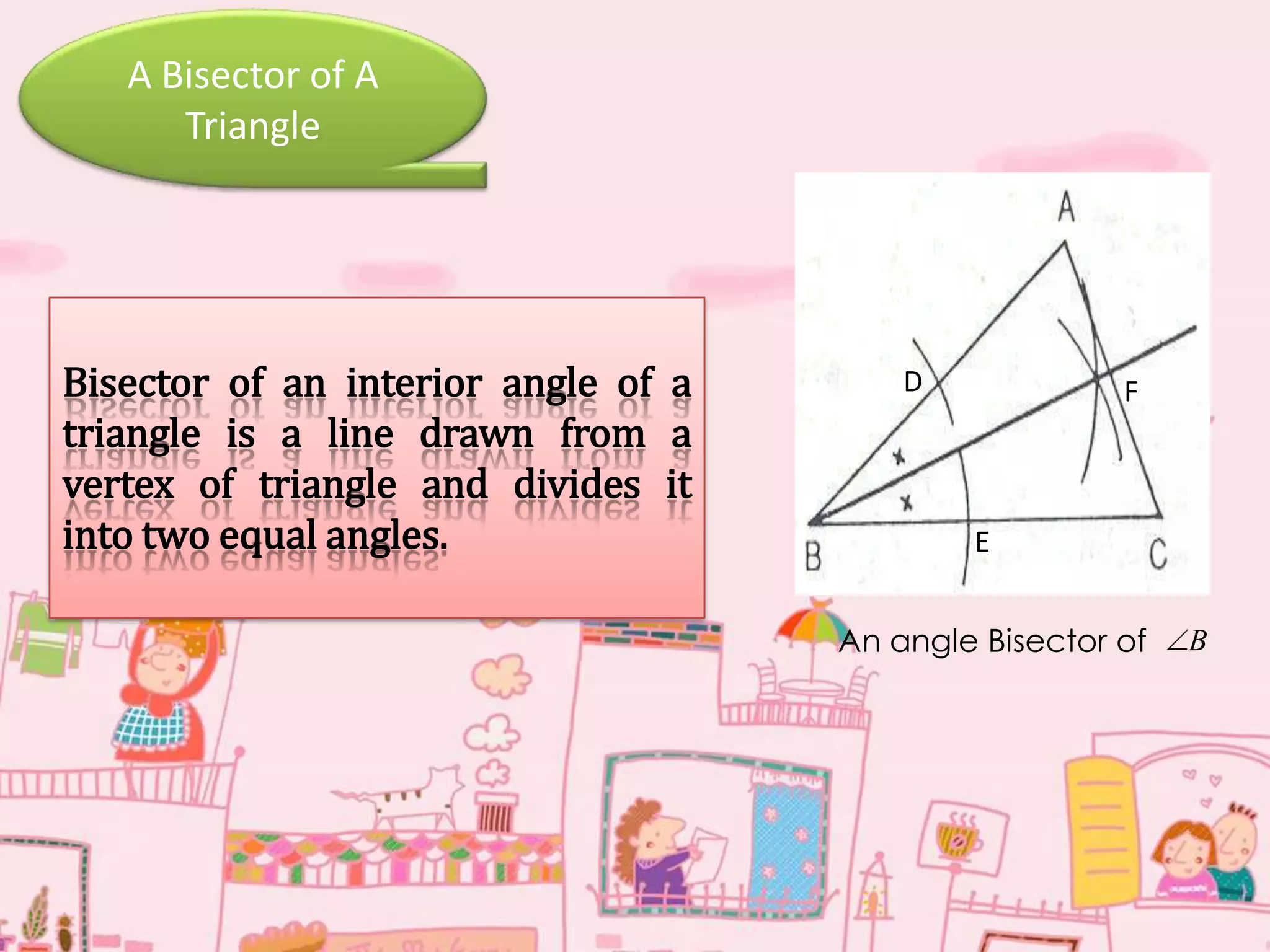
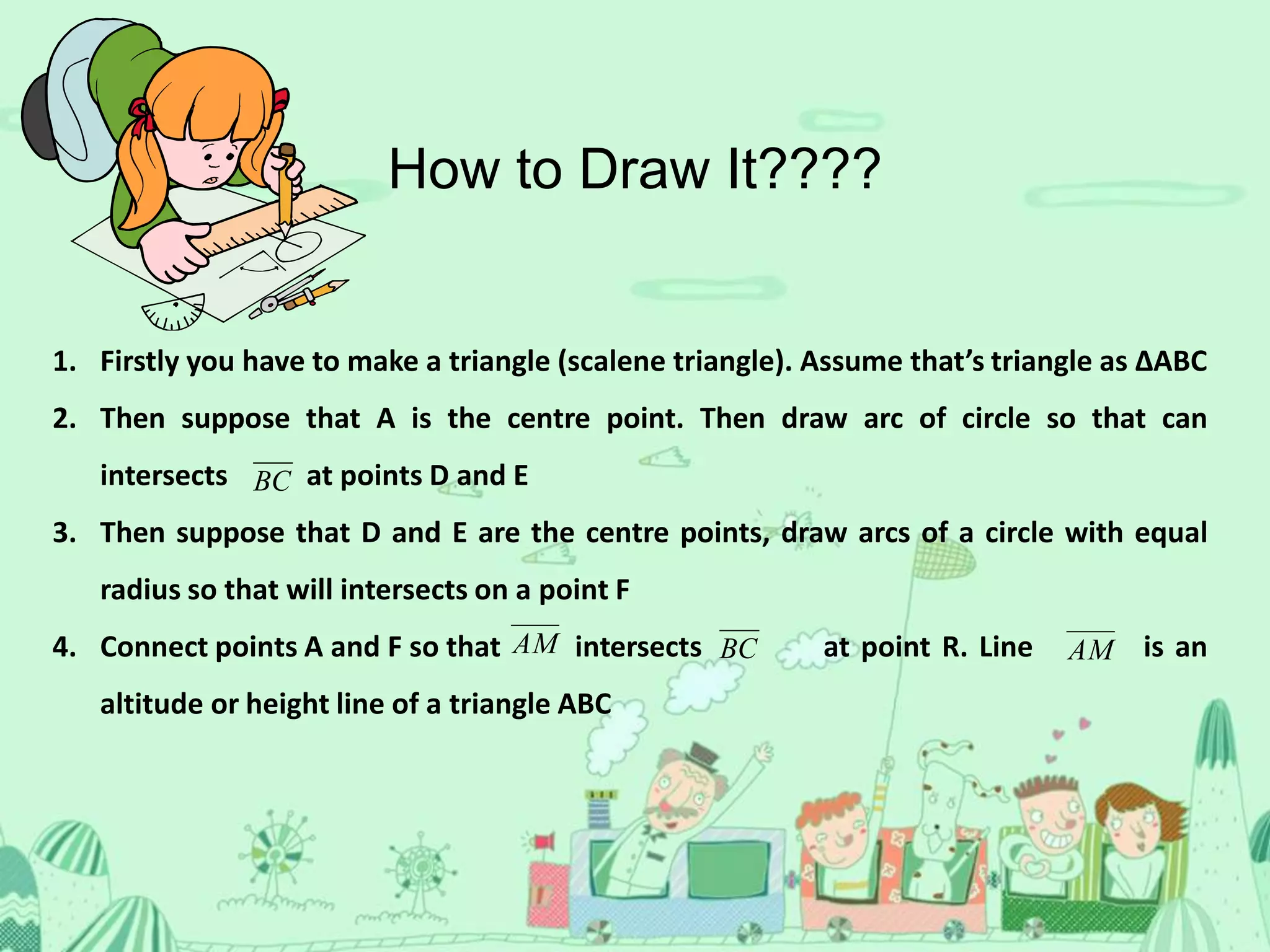
There are four types of lines that can be drawn in a triangle: 1. A perpendicular bisector of a side bisects the side at a 90 degree angle. 2. An angle bisector bisects the interior angle of the triangle into two equal angles. 3. A height or altitude drops perpendicular from a vertex to the opposite side. 4. A median connects a vertex to the midpoint of the opposite side.

1. TRIANGLE

3. There are four kinds of line in a triangle
A Perpendicular
Bisector of A
triangle
A Bisector of A
Triangle
A Height of A
Triangle
A Median of A
Triangle

4. A Perpendicular
Bisector of A triangle
Perpendicular Bisector of AB
Perpendicular bisector of a triangle is
a perpendicular line that intersects
the midpoint of a side.

6. 1. Firstly you have to make a triangle (scalene triangle). Assume that’s triangle as ∆ABC
2. Then suppose that A and B are the centre points. Then you can draw arcs of circle
above and below of the side of
3. Give a label of intersect point of those intersect points with D and E. Then connect
both points, so intersects to be an equal parts and also is
perpendicular to .
AB
DE AB DE
AB
How to Draw It????

7. A Bisector of A
Triangle
An angle Bisector of B
Bisector of an interior angle of a
triangle is a line drawn from a
vertex of triangle and divides it
into two equal angles.
D
E
F

9. 1. Firstly you have to make a triangle (scalene triangle). Assume that’s triangle as ∆ABC
2. Then suppose that B is the centre point. Then draw arcs of circle that intersects
on point D and it also intersects on point E
3. With D and E as the centre points, draw a circular arc with equal radius so that
those circular arcs intersect on point F
4. Connect the point s B and F, so it will be as a bisector of
AB
BF
BC
ABC
How to Draw It????

10. A Height or An
Altitude of A Triangle
A Height of A of ∆ABC

12. 1. Firstly you have to make a triangle (scalene triangle). Assume that’s triangle as ∆ABC
2. Then suppose that A is the centre point. Then draw arc of circle so that can
intersects at points D and E
3. Then suppose that D and E are the centre points, draw arcs of a circle with equal
radius so that will intersects on a point F
4. Connect points A and F so that intersects at point R. Line is an
altitude or height line of a triangle ABC
BC
AMBCAM
How to Draw It????

13. A Median of A
Triangle
A Median of BC
E
D
Q

15. 1. Firstly you have to make a triangle (scalene triangle). Assume that’s triangle as ∆ABC
2. Then suppose that B and C are the centre points. Then you can draw arcs of circle
above and below of the side of
3. Give a label of intersect point of those intersect points with D and E. Then connect
both points, so intersects on point Q
4. Connect points A and q. then line is a median of ∆ABC
BC
DE AB
PQ
How to Draw It????

16. SIMILARITY AND
CONGRUENCE OF
TRIANGLE

18. Definition: Similar triangles are triangles that have
the same shapes but not necessarily the same sizes.
A
C
B
D
F
E
ABC DEF
When we say that triangles are similar there are several
requirements that come from it.
A D
B E
C F
AB
DE
BC
EF
AC
DF
= =

19. 1. PPP Similarity Theorem
 3 pairs of proportional sides
Six of those statements are true as a result of the
similarity of the two triangles. However, if we need to
prove that a pair of triangles are similar, how many of
those statements do we need? Because we are working
with triangles and the measure of the angles and sides
are dependent on each other. We do not need all six.
There are three special combinations as requirements
that we can use to prove similarity of triangles.
2. PAP Similarity Theorem
 2 pairs of proportional sides and congruent
angles between them
3. AA Similarity Theorem
 2 pairs of congruent angles

20. 1. PPP Similarity Theorem
 3 pairs of proportional sidesA
B C
E
F D
251
4
5
.
DFm
ABm
251
69
12
.
.FEm
BCm
251
410
13
.
.DEm
ACm
5
4
12
9.6
ABC DFE

21. 2. PAP Similarity Theorem
 2 pairs of proportional sides and congruent
angles between them
G
H I
L
J K
660
57
5
.
.LKm
GHm
660
510
7
.
.KJm
HIm
7
10.5
70
70
m H = m K
GHI LKJ

22. The PAP Similarity Theorem does not work unless
the congruent angles fall between the proportional
sides. For example, if we have the situation that is
shown in the diagram below, we cannot state that the
triangles are similar. We do not have the information
that we need.
G
H I
L
J K
7
10.5
50
50
Angles I and J do not fall in between sides GH and HI and
sides LK and KJ respectively.

23. 3. AA Similarity Theorem
 2 pairs of congruent angles
M
N O
Q
P R
70
70
50
50
m N = m R
m O = m P MNO QRP

24. It is possible for two triangles to be similar when
they have 2 pairs of angles given but only one of
those given pairs are congruent.
87
34
34
S
T
U
XY
Z
m T = m X
m S = 180 - (34 + 87 )
m S = 180 - 121
m S = 59
m S = m Z
TSU XZY
59
5959
34
34

25. Congruent Triangles

26. Two triangles are congruent if the
sizes and shapes are same.
The definition of Congruent
Triangle
A C
B
DE
F

27. How much do you
need to know. . .
. . . about two triangles
that they
are congruent?

28. If all six pairs of corresponding parts (sides and
angles) are congruent, then the triangles are
congruent.
The symbol of congruent “ “.
Corresponding Parts
ABC DEF
1. AB DE
2. BC EF
3. AC DF
4. A D
5. B E
6. C F

29. Do you need all six ?
NO !
SSS
SAS
ASA
Some conditions or requirement
that are needed for a congruent triangle. They
are:
The Requirements

30. Side-Side-Side (SSS)
1.
2.
3.
ABC DEF
DEAB
EFBC
DFAC

31. Incuded Angle is The angle between
two sides
Included Angle
G I H

32. Included Angle
SY
E
Name the included angle
between two sides following
below:
and is
and is
and is
E
S
Y
YE ES
YSES
YS YE

33. Side-Angle-Side (SAS)
ABC DEF
included
angle
DEAB.1
DFAC.3
DA.2

34. Included side is the side between
two angles
Included Side
GI HI GH

35. Name the included angle
between two angles following
below:
Y and E is
E and S is
S and Y is
Included Side
SY
E
YE
ES
SY

36. Angle-Side-Angle (ASA)
1. A D
2. AB DE
3. B E
ABC DEF
included
side

37. Name That requirement
SAS
ASA
(when possible)
SSS

38. Let’s Practice
Indicate the additional information needed to
enable us to show that those two triangles are
congruent.
For ASA:
For SAS:
B D
AC FE

39. HW
For ASA:
For SAS:
Indicate the additional information needed to
enable us to show that those two triangles are
congruent.

40. THANKS
THANKS