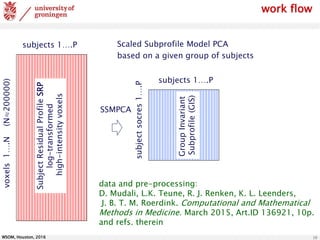
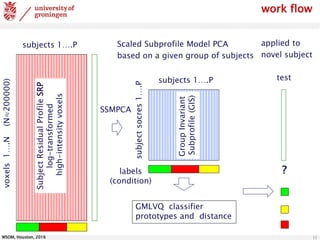
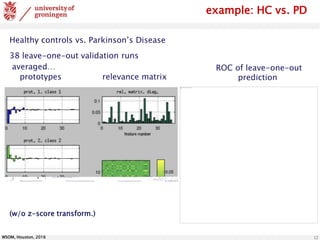
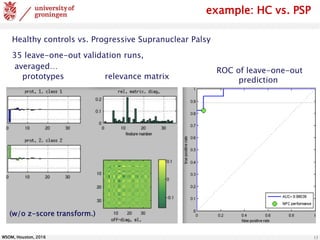
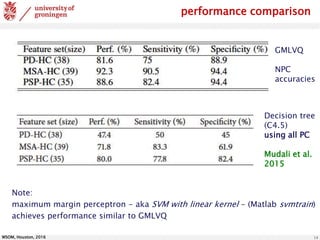
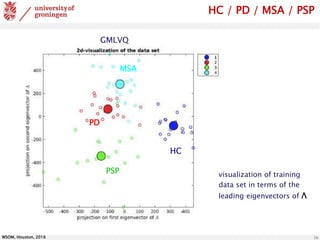
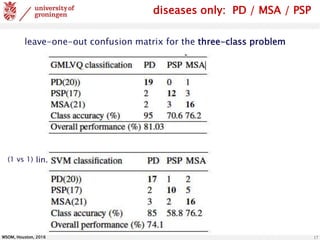
The document discusses the classification of brain data using FDG-PET scans to differentiate between various parkinsonian syndromes through advanced machine learning techniques like Generalized Matrix Relevance Learning Vector Quantization (GMLVQ) and Principal Component Analysis (PCA). The research highlights the benefits of prototype-based classification methods for improved accuracy compared to traditional decision trees, particularly in multi-class scenarios involving healthy controls and patients with Parkinson's disease, multiple system atrophy, and progressive supranuclear palsy. Future work involves optimizing feature selection and understanding relevance in voxel-space to further enhance classifier performance.

1. Classification of FDG-PET* Brain Data
* Fluorodeoxyglucose positron emission tomography
Deborah Mudali 1,* Michael Biehl 1
Klaus L. Leenders 2 Jos B.T.M. Roerdink 1,3
1 Johann Bernoulli Institute for Mathematics
and Computer Science, University of Groningen, NL
2 Department of Neurology
University Medical Center Groningen, NL
3 Neuroimaging Center
University Medical Center Groningen, NL
* Mbarara University of Science & Technology, Uganda

2. WSOM, Houston, 2016 2
overview
Example application
Classification of Parkinsonian Syndromes
based on FDG-PET brain data
Combination: PCA + GMLVQ
comparison with DT, SVM
Conclusion and Outlook
Prototype-based classification
Learning Vector Quantization
Generalized Matrix Relevance Learning (GMLVQ)

3. WSOM, Houston, 2016
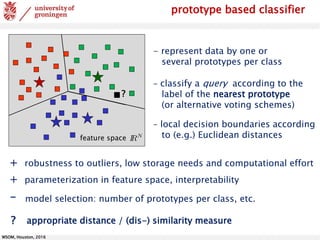
∙ identification of prototype vectors from labeled example data
∙ (dis)-similarity based classification (e.g. Euclidean distance)
Learning Vector Quantization
N-dimensional data, feature vectors
• initialize prototype vectors
for different classes
competitive learning: Winner-Takes-All LVQ1 [Kohonen, 1990, 1997]
• identify the winner
(closest prototype)
• present a single example
• move the winner
- closer towards the data (same class)
- away from the data (different class)
feature space

4. WSOM, Houston, 2016
prototype based classifier
- represent data by one or
several prototypes per class
- classify a query according to the
label of the nearest prototype
(or alternative voting schemes)
- local decision boundaries according
to (e.g.) Euclidean distances
+ robustness to outliers, low storage needs and computational effort
- model selection: number of prototypes per class, etc.
feature space
?
? appropriate distance / (dis-) similarity measure
+ parameterization in feature space, interpretability

5. WSOM, Houston, 2016 5
fixed distance measures:
- choice based on prior knowledge or preprocessing
- determine prototypes from example data
by means of (iterative) learning schemes
e.g. heuristic LVQ1, cost function based Generalized LVQ
relevance learning, adaptive distances:
- employ parameterized distance measure
- update parameters in one training process with prototypes
- optimize adaptive, data driven dissimilarity
example: Matrix Relevance LVQ
Learning Vector Quantization

6. WSOM, Houston, 2016
Relevance Matrix LVQ
generalized quadratic distance in LVQ:
variants: global/local matrices (piecewise quadratic boundaries)
diagonal relevances (single feature weights)
rectangular (low-dim. representation)
[Schneider et al., 2009]
relevance matrix:
quantifies importance of features and pairs of features
summarizes relevance of feature j
( for equally scaled features )
training: optimize prototypes and Λ w.r.t. classification of examples

7. WSOM, Houston, 2016
cost function based training
one example: Generalized LVQ [Sato & Yamada, 1995]
sigmoidal (linear for small arguments), e.g.
E approximates number of misclassifications
linear
E favors large margin separation of classes, e.g.
two winning prototypes:
minimize
small , large
E favors class-typical prototypes

8. WSOM, Houston, 2016
cost function based LVQ
There is nothing objective about objective functions
James McClelland

9. WSOM, Houston, 2016 9
FDG-PET (Fluorodeoxyglucose positron emission tomography, 3d-images)
condition
Glucoseuptake
n=18 HC
Healhy controls
n= 20 PD
Parkinson’s Disease
n=21 MSA
Multiple System Atrophy
n=17 PSP
Progressive Supranuclear
Palsy
classification of FDG-PET data
[http://glimpsproject.com]

10. WSOM, Houston, 2016 10
work flow
subjects 1….P
voxels1….N(N≈200000)
SubjectResidualProfileSRP
log-transformed
high-intensityvoxels
GroupInvariant
Subprofile(GIS)
subjectsocres1….P
subjects 1….P
Scaled Subprofile Model PCA
based on a given group of subjects
SSMPCA
data and pre-processing:
D. Mudali, L.K. Teune, R. J. Renken, K. L. Leenders,
J. B. T. M. Roerdink. Computational and Mathematical
Methods in Medicine. March 2015, Art.ID 136921, 10p.
and refs. therein

11. WSOM, Houston, 2016 11
work flow
subjects 1….P
voxels1….N(N≈200000)
SubjectResidualProfileSRP
log-transformed
high-intensityvoxels
GroupInvariant
Subprofile(GIS)
subjectsocres1….P
subjects 1….P
Scaled Subprofile Model PCA
based on a given group of subjects
applied to
novel subject
test
labels
(condition)
GMLVQ classifier
prototypes and distance
?
SSMPCA

12. WSOM, Houston, 2016 12
Healthy controls vs. Parkinson’s Disease
38 leave-one-out validation runs
averaged…
prototypes relevance matrix
ROC of leave-one-out
prediction
example: HC vs. PD
(w/o z-score transform.)

13. WSOM, Houston, 2016 13
Healthy controls vs. Progressive Supranuclear Palsy
35 leave-one-out validation runs,
averaged…
prototypes relevance matrix
example: HC vs. PSP
ROC of leave-one-out
prediction
(w/o z-score transform.)

14. WSOM, Houston, 2016 14
GMLVQ
NPC
accuracies
Note:
maximum margin perceptron - aka SVM with linear kernel - (Matlab svmtrain)
achieves performance similar to GMLVQ
performance comparison
Decision tree
(C4.5)
using all PC
Mudali et al.
2015

15. WSOM, Houston, 2016 15
four classes: HC / PD / MSA / PSP
leave-one-out confusion matrix for the four-class problem
GM
lin.
77.8 %
65.0 %
64.7 %
76.2 %
class acc.
66.7 %
60.0 %
52.9 %
89.0 %
class acc.(1 vs 1)

16. WSOM, Houston, 2016 16
HC / PD / MSA / PSP
HC
PSP
PD
MSA
GMLVQ
visualization of training
data set in terms of the
leading eigenvectors of Λ

17. WSOM, Houston, 2016 17
diseases only: PD / MSA / PSP
leave-one-out confusion matrix for the three-class problem
lin.(1 vs 1)

18. WSOM, Houston, 2016 18
diseases only: PD / MSA / PSP
MSA
PD
PSP
GMLVQ
visualization of training
data set in terms of the
leading eigenvectors of Λ

19. WSOM, Houston, 2016 19
discussion / conclusion
- detection and discrimination of Parkinsonian syndromes:
GMLVQ classifier and SVM clearly outperform decision trees
decision trees
- serious limitations:
small data set
leave-one-out validation
over-fitting
- accuracy is not enough:
can we obtain better insight into the classifiers ?

20. WSOM, Houston, 2016 20
outlook/work in progress
- optimization of the number of PCs used as features
shown to improve decision tree performance
potential improvement for other classifiers
- larger data sets
- understanding relevances in voxel-space
relevant PC hint at discriminative between-patient variability
PCA:
recent example:
diagnosis of rheumatoid arthritis based on cytokine expression
[L. Yeo et al., Ann. of the Rheumatic Diseases, 2015]

21. WSOM, Houston, 2016 21
http://matlabserver.cs.rug.nl/gmlvqweb/web/
Matlab code:
Relevance and Matrix adaptation in Learning Vector
Quantization (GRLVQ, GMLVQ and LiRaM LVQ):
http://www.cs.rug.nl/~biehl/
links
Pre- and re-prints etc.:
A no-nonsense beginners’ tool for GMLVQ:
http://www.cs.rug.nl/~biehl/gmlvq

22. WSOM, Houston, 2016
Questions ?