The document discusses the statistical physics perspective on learning, particularly focusing on student/teacher models and the typical learning curves associated with them. It covers topics like stochastic optimization, phase transitions in neural networks, and the complexities involved in training, including high temperature limits and the interplay between training error and generalization error. Additionally, it examines specific systems like soft-committee machines to illustrate the concepts involved in neural network training and optimization.

1. 1
The statistical physics approach to
the theory of learning
Typical learning curves in student / teacher models
www.cs.rug.nl/~biehl
Michael Biehl
APPIS 2023

2. 1
The statistical physics approach to
the theory of learning
Typical learning curves in student / teacher models
www.cs.rug.nl/~biehl
Michael Biehl
APPIS 2023
•statistical physics of stochastic optimizaton

3. 1
The statistical physics approach to
the theory of learning
Typical learning curves in student / teacher models
www.cs.rug.nl/~biehl
Michael Biehl
APPIS 2023
•statistical physics of stochastic optimizaton
•machine learning specifics, disorder average over data sets

4. 1
The statistical physics approach to
the theory of learning
Typical learning curves in student / teacher models
www.cs.rug.nl/~biehl
Michael Biehl
APPIS 2023
•statistical physics of stochastic optimizaton
•machine learning specifics, disorder average over data sets
•a simplifying limit: training at high temperature

5. 1
The statistical physics approach to
the theory of learning
Typical learning curves in student / teacher models
www.cs.rug.nl/~biehl
Michael Biehl
APPIS 2023
•statistical physics of stochastic optimizaton
•machine learning specifics, disorder average over data sets
•a simplifying limit: training at high temperature
•student / teacher models

6. 1
The statistical physics approach to
the theory of learning
Typical learning curves in student / teacher models
www.cs.rug.nl/~biehl
Michael Biehl
APPIS 2023
•statistical physics of stochastic optimizaton
•machine learning specifics, disorder average over data sets
•a simplifying limit: training at high temperature
•student / teacher models
•example: phase transitions in (shallow) layered neural networks

7. 2
Statistical Physics of Neural Networks
John Hopfield
Neural Networks and physical systems with emergent
collective computational abilities
PNAS 79(8): 2554, 1982
[activity of model neurons for given synaptic weights]

8. 2
Statistical Physics of Neural Networks
John Hopfield
Neural Networks and physical systems with emergent
collective computational abilities
PNAS 79(8): 2554, 1982
[activity of model neurons for given synaptic weights]
Elizabeth Gardner (1957-1988)
The space of interactions in neural networks
J. Phys. A 21: 257, 1988
[synaptic weights determined for given activity patterns]

9. 3
stochastic optimization
objective/cost/ energy function , e.g. (later: )
consider stochastic optimization process, for example:
H(w) w ∈ ℝN
N → ∞

10. 3
stochastic optimization
objective/cost/ energy function , e.g. (later: )
consider stochastic optimization process, for example:
H(w) w ∈ ℝN
N → ∞
Metropolis-like updates: small random changes of
accepted with probability
Δw w
min{1, exp[−βΔH]}

11. 3
stochastic optimization
objective/cost/ energy function , e.g. (later: )
consider stochastic optimization process, for example:
H(w) w ∈ ℝN
N → ∞
Metropolis-like updates: small random changes of
accepted with probability
Δw w
min{1, exp[−βΔH]}
Langevin dynamics: noisy gradient descent
∂w
∂t
= − ∇wH(w) + f(t)
⟨fj(t)fk(s)⟩ =
2
β
δjkδ(t − s)
with delta-correlated noise:

12. 3
stochastic optimization
objective/cost/ energy function , e.g. (later: )
consider stochastic optimization process, for example:
H(w) w ∈ ℝN
N → ∞
Metropolis-like updates: small random changes of
accepted with probability
Δw w
min{1, exp[−βΔH]}
Langevin dynamics: noisy gradient descent
∂w
∂t
= − ∇wH(w) + f(t)
⟨fj(t)fk(s)⟩ =
2
β
δjkδ(t − s)
with delta-correlated noise:
… acceptance rate for uphill moves in Metropolis algorithms
... noise level, i.e. random deviation from gradient
… “how serious we are about minimizing ”
H
temperature-like parameter controls

13. thermal equilibrium
stationary density of configurations:
normalization:
Zustandssumme, partition function
4
P(w) =
1
Z
exp [−βH(w)]
Z =
∫
dN
w exp [−βH(w)]

14. thermal equilibrium
stationary density of configurations:
normalization:
Zustandssumme, partition function
Gibbs-Boltzmann density of states
• physics: thermal equilibrium of a physical system at temperature T
• optimization: formal equilibrium situation, control parameter T
4
P(w) =
1
Z
exp [−βH(w)]
Z =
∫
dN
w exp [−βH(w)]

15. thermal equilibrium
stationary density of configurations:
normalization:
Zustandssumme, partition function
Gibbs-Boltzmann density of states
• physics: thermal equilibrium of a physical system at temperature T
• optimization: formal equilibrium situation, control parameter T
4
P(w) =
1
Z
exp [−βH(w)]
• thermal averages, e.g.
equilibrium properties given by (derivatives of) ln Z
E = ⟨H⟩T
=
∫
dN
w H(w) P(w) = −
∂
∂β
ln Z
Z =
∫
dN
w exp [−βH(w)]

16. 5
~ volume of states with energy E
Z =
∫
dN
w exp[−β(Hw)] =
∫
dE
∫
dN
w δ[H(w) − E] e−βE
free energy

17. 5
~ volume of states with energy E
Z =
∫
dN
w exp[−β(Hw)] =
∫
dE
∫
dN
w δ[H(w) − E] e−βE
assume extensive energy , for
E = Ne N → ∞
Z =
∫
dE exp [−Nβ (e − s(e)/β)]
entropy ,
s(E)
f = e − s/β ∼ − ln Z/(βN)
dominated by the minimum of the
free energy
free energy

18. 5
~ volume of states with energy E
Z =
∫
dN
w exp[−β(Hw)] =
∫
dE
∫
dN
w δ[H(w) − E] e−βE
assume extensive energy , for
E = Ne N → ∞
Z =
∫
dE exp [−Nβ (e − s(e)/β)]
entropy ,
s(E)
f = e − s/β ∼ − ln Z/(βN)
dominated by the minimum of the
free energy
free energy
controls the competition between
minimization of energy e and
maximization of entropy s(e)
T = 1/β

19. 6
machine learning
ID = {ξμ
, τμ
= τ(ξμ
)}
P
μ=1
H(w) =
P
∑
μ=1
ϵ(σμ
, τμ
)
specifically:
extensive ( ) for
∼ N P = αN
compares student outputs σμ
= σ(ξμ
) and targets τμ
= τ(ξμ
)
energy: defined with respect a given data set

20. 6
machine learning
ID = {ξμ
, τμ
= τ(ξμ
)}
P
μ=1
H(w) =
P
∑
μ=1
ϵ(σμ
, τμ
)
specifically:
extensive ( ) for
∼ N P = αN
compares student outputs σμ
= σ(ξμ
) and targets τμ
= τ(ξμ
)
energy: defined with respect a given data set

21. 6
machine learning
ID = {ξμ
, τμ
= τ(ξμ
)}
P
μ=1
H(w) =
P
∑
μ=1
ϵ(σμ
, τμ
)
typical results on average over data sets ID
•specific input density, e.g. i.i.d. zero mean, unit variance ξμ
j
•training labels provided by teacher network
τμ
, consider
specifically:
extensive ( ) for
∼ N P = αN
compares student outputs σμ
= σ(ξμ
) and targets τμ
= τ(ξμ
)
energy: defined with respect a given data set

22. 6
machine learning
ID = {ξμ
, τμ
= τ(ξμ
)}
P
μ=1
H(w) =
P
∑
μ=1
ϵ(σμ
, τμ
)
typical results on average over data sets ID
•specific input density, e.g. i.i.d. zero mean, unit variance ξμ
j
•training labels provided by teacher network
τμ
, consider
disorder average:
quenched free energy ∼ ⟨ln Z⟩ID
technically difficult for general T = 1/β
specifically:
extensive ( ) for
∼ N P = αN
compares student outputs σμ
= σ(ξμ
) and targets τμ
= τ(ξμ
)
energy: defined with respect a given data set

23. 6
machine learning
ID = {ξμ
, τμ
= τ(ξμ
)}
P
μ=1
H(w) =
P
∑
μ=1
ϵ(σμ
, τμ
)
typical results on average over data sets ID
•specific input density, e.g. i.i.d. zero mean, unit variance ξμ
j
•training labels provided by teacher network
τμ
, consider
disorder average:
quenched free energy ∼ ⟨ln Z⟩ID
technically difficult for general T = 1/β
specifically:
e.g. by means of the replica trick/method Giorgio Parisi, Nobel 2021
extensive ( ) for
∼ N P = αN
compares student outputs σμ
= σ(ξμ
) and targets τμ
= τ(ξμ
)
energy: defined with respect a given data set

24. 7
high temperature limit
a simplifying limit: training at high temperature
lim
β→0
: ⟨ln Z⟩ID
= ln ⟨Z⟩ID ⟨H(w) ⟩ID
= P ⟨ϵ(σ, τ)⟩ξ
= P ϵg
generalization error

25. 7
high temperature limit
a simplifying limit: training at high temperature
lim
β→0
: ⟨ln Z⟩ID
= ln ⟨Z⟩ID
βf = β (P/N) ϵg − s(ϵg)
⟨H(w) ⟩ID
= P ⟨ϵ(σ, τ)⟩ξ
= P ϵg
generalization error

26. 7
high temperature limit
a simplifying limit: training at high temperature
lim
β→0
: ⟨ln Z⟩ID
= ln ⟨Z⟩ID
βf = β (P/N) ϵg − s(ϵg)
⟨H(w) ⟩ID
= P ⟨ϵ(σ, τ)⟩ξ
= P ϵg
generalization error
β → 0
P/N → ∞
⏟
α = 𝒪(1)
“learn almost nothing from
infinitely many examples”

27. 7
high temperature limit
a simplifying limit: training at high temperature
lim
β→0
: ⟨ln Z⟩ID
= ln ⟨Z⟩ID
βf = β (P/N) ϵg − s(ϵg)
⟨H(w) ⟩ID
= P ⟨ϵ(σ, τ)⟩ξ
= P ϵg
generalization error
β → 0
P/N → ∞
⏟
α = 𝒪(1)
“learn almost nothing from
infinitely many examples”
min. free energy typical learning curve ϵg(α)

28. 7
high temperature limit
a simplifying limit: training at high temperature
lim
β→0
: ⟨ln Z⟩ID
= ln ⟨Z⟩ID
βf = β (P/N) ϵg − s(ϵg)
⟨H(w) ⟩ID
= P ⟨ϵ(σ, τ)⟩ξ
= P ϵg
generalization error
β → 0
P/N → ∞
⏟
α = 𝒪(1)
“learn almost nothing from
infinitely many examples”
limitations:
- training error and generalization error cannot be distinguished
- number of examples and training temperature are coupled
- (at best) qualitative agreement with low temperature results
min. free energy typical learning curve ϵg(α)

29. 8
student/teacher scenarios
example system: soft-committee machines (SCM)
adaptive student N-dim. inputs
<latexit
sha1_base64="EWEUTU/uT8q6Rkb2wo5Q65mhUMs=">AAACQXicbVDPaxQxFM5Ubetq66pHL8FF2l6WmaJYCoWCIEKhtOBuFzbbIZPJzIZNJtPkjbqE+de8ePDupfTeSw9K8erFzG4P/fVByMf3vcd770tKKSyE4Vmw8ODho8Wl5cetJ09XVp+1n7/oW10ZxntMS20GCbVcioL3QIDkg9JwqhLJj5LJh8Y/+sKNFbr4DNOSjxTNC5EJRsFLcXtArMgVxTuY2ErFbrIT1cd7OCeSZ7BOMkOZI4rCOMnc1zqeYMJSDZgkWqZ2qvznyDdR147YEwNuv66JEfkYNuJ2J+yGM+C7JLoind3ttdNj/PHnQdz+RVLNKsULYJJaO4zCEkaOGhBM8rpFKstLyiY050NPC6q4HblZAjV+45UUZ9r4VwCeqdc7HFW2WddXNsfY214j3ucNK8i2Rk4UZQW8YPNBWSUxaNzEiVNhOAM59YQyI/yumI2pTw186C0fQnT75Lukv9mN3nXDQ5/GWzTHMnqFXqN1FKH3aBd9Qgeohxj6js7Rb/Qn+BFcBJfB33npQnDV8xLdQPDvP9i7tUY=</latexit>
=
K
X
k=1
g
✓
wk · ⇠
p
N
◆

30. 8
student/teacher scenarios
example system: soft-committee machines (SCM)
adaptive student N-dim. inputs
•non-linear hidden unit activations , fixed linear output
g(z)
<latexit
sha1_base64="EWEUTU/uT8q6Rkb2wo5Q65mhUMs=">AAACQXicbVDPaxQxFM5Ubetq66pHL8FF2l6WmaJYCoWCIEKhtOBuFzbbIZPJzIZNJtPkjbqE+de8ePDupfTeSw9K8erFzG4P/fVByMf3vcd770tKKSyE4Vmw8ODho8Wl5cetJ09XVp+1n7/oW10ZxntMS20GCbVcioL3QIDkg9JwqhLJj5LJh8Y/+sKNFbr4DNOSjxTNC5EJRsFLcXtArMgVxTuY2ErFbrIT1cd7OCeSZ7BOMkOZI4rCOMnc1zqeYMJSDZgkWqZ2qvznyDdR147YEwNuv66JEfkYNuJ2J+yGM+C7JLoind3ttdNj/PHnQdz+RVLNKsULYJJaO4zCEkaOGhBM8rpFKstLyiY050NPC6q4HblZAjV+45UUZ9r4VwCeqdc7HFW2WddXNsfY214j3ucNK8i2Rk4UZQW8YPNBWSUxaNzEiVNhOAM59YQyI/yumI2pTw186C0fQnT75Lukv9mN3nXDQ5/GWzTHMnqFXqN1FKH3aBd9Qgeohxj6js7Rb/Qn+BFcBJfB33npQnDV8xLdQPDvP9i7tUY=</latexit>
=
K
X
k=1
g
✓
wk · ⇠
p
N
◆

31. 8
•complexity (mis-)match: vs. hidden units, here
K M K = M
student/teacher scenarios
example system: soft-committee machines (SCM)
adaptive student N-dim. inputs teacher parameterizes target
? ? ? ? ? ? ?
<latexit
sha1_base64="ALwOwp1y3TncZZzQCxrhKlQLkC0=">AAACQXicbVA9TxwxEPVCCHBAckCZxgIhAcVpN0oEFEhIaWiIiJSDk87Hyuv13lnY68WeBS7W/hz+Bg3/gI6eJkWiKG2aeO8o+HqS5af3ZjQzLymksBCGd8HE5Jupt9Mzs425+YV375uLS0dWl4bxNtNSm05CLZci520QIHmnMJyqRPLj5PRL7R+fc2OFzr/DsOA9Rfu5yASj4KW42SFAS7yLiS1V7NRuVJ0c4D6RPIN1khnKHFEUBknmLqpYnWxiwlINmCRapnao/OfIpagqR+yZAfe1qogR/QFsxM3VsBWOgF+S6IGs7u3A1Y9LuXIYN29JqlmpeA5MUmu7UVhAz1EDgkleNUhpeUHZKe3zrqc5Vdz23CiBCq95JcWZNv7lgEfq4w5Hla3X9ZX1Ofa5V4uved0Ssu2eE3lRAs/ZeFBWSgwa13HiVBjOQA49ocwIvytmA+pzAx96w4cQPT/5JTn62Io+t8JvPo1PaIwZ9AGtoHUUoS20h/bRIWojhq7RPfqFfgc3wc/gT/B3XDoRPPQsoycI/v0HjhS1HA==</latexit>
⌧ =
M
X
m=1
g
✓
w⇤
m · ⇠
p
N
◆
•non-linear hidden unit activations , fixed linear output
g(z)
<latexit
sha1_base64="EWEUTU/uT8q6Rkb2wo5Q65mhUMs=">AAACQXicbVDPaxQxFM5Ubetq66pHL8FF2l6WmaJYCoWCIEKhtOBuFzbbIZPJzIZNJtPkjbqE+de8ePDupfTeSw9K8erFzG4P/fVByMf3vcd770tKKSyE4Vmw8ODho8Wl5cetJ09XVp+1n7/oW10ZxntMS20GCbVcioL3QIDkg9JwqhLJj5LJh8Y/+sKNFbr4DNOSjxTNC5EJRsFLcXtArMgVxTuY2ErFbrIT1cd7OCeSZ7BOMkOZI4rCOMnc1zqeYMJSDZgkWqZ2qvznyDdR147YEwNuv66JEfkYNuJ2J+yGM+C7JLoind3ttdNj/PHnQdz+RVLNKsULYJJaO4zCEkaOGhBM8rpFKstLyiY050NPC6q4HblZAjV+45UUZ9r4VwCeqdc7HFW2WddXNsfY214j3ucNK8i2Rk4UZQW8YPNBWSUxaNzEiVNhOAM59YQyI/yumI2pTw186C0fQnT75Lukv9mN3nXDQ5/GWzTHMnqFXqN1FKH3aBd9Qgeohxj6js7Rb/Qn+BFcBJfB33npQnDV8xLdQPDvP9i7tUY=</latexit>
=
K
X
k=1
g
✓
wk · ⇠
p
N
◆

32. 8
•complexity (mis-)match: vs. hidden units, here
K M K = M
student/teacher scenarios
example system: soft-committee machines (SCM)
adaptive student N-dim. inputs teacher parameterizes target
? ? ? ? ? ? ?
<latexit
sha1_base64="ALwOwp1y3TncZZzQCxrhKlQLkC0=">AAACQXicbVA9TxwxEPVCCHBAckCZxgIhAcVpN0oEFEhIaWiIiJSDk87Hyuv13lnY68WeBS7W/hz+Bg3/gI6eJkWiKG2aeO8o+HqS5af3ZjQzLymksBCGd8HE5Jupt9Mzs425+YV375uLS0dWl4bxNtNSm05CLZci520QIHmnMJyqRPLj5PRL7R+fc2OFzr/DsOA9Rfu5yASj4KW42SFAS7yLiS1V7NRuVJ0c4D6RPIN1khnKHFEUBknmLqpYnWxiwlINmCRapnao/OfIpagqR+yZAfe1qogR/QFsxM3VsBWOgF+S6IGs7u3A1Y9LuXIYN29JqlmpeA5MUmu7UVhAz1EDgkleNUhpeUHZKe3zrqc5Vdz23CiBCq95JcWZNv7lgEfq4w5Hla3X9ZX1Ofa5V4uved0Ssu2eE3lRAs/ZeFBWSgwa13HiVBjOQA49ocwIvytmA+pzAx96w4cQPT/5JTn62Io+t8JvPo1PaIwZ9AGtoHUUoS20h/bRIWojhq7RPfqFfgc3wc/gT/B3XDoRPPQsoycI/v0HjhS1HA==</latexit>
⌧ =
M
X
m=1
g
✓
w⇤
m · ⇠
p
N
◆
•non-linear hidden unit activations , fixed linear output
g(z)
•given determine weights
ID = {ξμ
, τμ
= τ(ξμ
)}
P
μ=1
W = {wk}
K
k=1
H(W) =
1
P
P
∑
μ=1
ϵ(σμ
, τμ
) =
1
P
P
∑
μ=1
1
2
(σμ
− τμ
)2
<latexit
sha1_base64="EWEUTU/uT8q6Rkb2wo5Q65mhUMs=">AAACQXicbVDPaxQxFM5Ubetq66pHL8FF2l6WmaJYCoWCIEKhtOBuFzbbIZPJzIZNJtPkjbqE+de8ePDupfTeSw9K8erFzG4P/fVByMf3vcd770tKKSyE4Vmw8ODho8Wl5cetJ09XVp+1n7/oW10ZxntMS20GCbVcioL3QIDkg9JwqhLJj5LJh8Y/+sKNFbr4DNOSjxTNC5EJRsFLcXtArMgVxTuY2ErFbrIT1cd7OCeSZ7BOMkOZI4rCOMnc1zqeYMJSDZgkWqZ2qvznyDdR147YEwNuv66JEfkYNuJ2J+yGM+C7JLoind3ttdNj/PHnQdz+RVLNKsULYJJaO4zCEkaOGhBM8rpFKstLyiY050NPC6q4HblZAjV+45UUZ9r4VwCeqdc7HFW2WddXNsfY214j3ucNK8i2Rk4UZQW8YPNBWSUxaNzEiVNhOAM59YQyI/yumI2pTw186C0fQnT75Lukv9mN3nXDQ5/GWzTHMnqFXqN1FKH3aBd9Qgeohxj6js7Rb/Qn+BFcBJfB33npQnDV8xLdQPDvP9i7tUY=</latexit>
=
K
X
k=1
g
✓
wk · ⇠
p
N
◆
by minimizing costs

33. 9
SCM student/teacher
thermodynamic limit Central Limit Theorem (CLT) :
N → ∞
xk =
wk ⋅ ξ
N
x*
m =
w*
m ⋅ ξ
N
become zero mean Gaussians
with -dim covariance matrix
(M + K) × (M + K)

34. 9
SCM student/teacher
thermodynamic limit Central Limit Theorem (CLT) :
N → ∞
xk =
wk ⋅ ξ
N
x*
m =
w*
m ⋅ ξ
N
become zero mean Gaussians
with -dim covariance matrix
(M + K) × (M + K)
C =
2
6
6
6
6
6
6
6
6
4
T11 T12 . . . T1M R11 R21 . . . RK1
.
.
.
.
.
.
...
.
.
.
.
.
.
.
.
.
...
.
.
.
TM1 TM2 . . . TMM R1M R2M . . . RKM
R11 R12 . . . R1M Q11 Q12 . . . Q1K
.
.
.
.
.
.
...
.
.
.
.
.
.
.
.
.
...
.
.
.
RK1 RK2 . . . RKM QK1 QK2 . . . QKK
3
7
7
7
7
7
7
7
7
5
=

T R
R>
Q
Rim = wi · w⇤
m/N
Qik = wi · wk/N
Tmn = w⇤
m · w⇤
n/N
order parameters: model parameters:
macroscopic
properties of
the system
Qik = Qki
Tmn = Tnm

35. 9
SCM student/teacher
thermodynamic limit Central Limit Theorem (CLT) :
N → ∞
xk =
wk ⋅ ξ
N
x*
m =
w*
m ⋅ ξ
N
become zero mean Gaussians
with -dim covariance matrix
(M + K) × (M + K)
C =
2
6
6
6
6
6
6
6
6
4
T11 T12 . . . T1M R11 R21 . . . RK1
.
.
.
.
.
.
...
.
.
.
.
.
.
.
.
.
...
.
.
.
TM1 TM2 . . . TMM R1M R2M . . . RKM
R11 R12 . . . R1M Q11 Q12 . . . Q1K
.
.
.
.
.
.
...
.
.
.
.
.
.
.
.
.
...
.
.
.
RK1 RK2 . . . RKM QK1 QK2 . . . QKK
3
7
7
7
7
7
7
7
7
5
=

T R
R>
Q
Rim = wi · w⇤
m/N
Qik = wi · wk/N
Tmn = w⇤
m · w⇤
n/N
order parameters: model parameters:
macroscopic
properties of
the system
⟨…⟩ξ
→ ⟨…⟩
{xk,x*
m}
averages:
Qik = Qki
Tmn = Tnm
Gaussian integrals!

36. 10
simplification: orthonormal teacher vectors, isotropic input density
reflects permutation symmetry, allows for hidden unit specialization
Tij =
⇢
1 for i = j
0 else,
Rij =
⇢
R for i = j
S else,
Qij =
⇢
1 for i = j
C else.
<latexit
sha1_base64="z3U/1x66FQ8CCAKv5dCLWIcbiuE=">AAADPXicpVI7b9RAEF6bQBLzukBJMyICUSDLTiSSJlIgDWVel0S6PZ3We+O7TdZra3eNOFm+X5Ffk4aCf0BHR0PBQ4guLeu7gMhDCMRIK3365vHNzE5SSGFsFL33/Gsz12/Mzs0HN2/dvnO3tXBvz+Sl5tjmucz1QcIMSqGwbYWVeFBoZFkicT852mj8+69QG5GrXTsqsJuxgRKp4Mw6qrfg7ez2KnFYwxoAlZhaWgFNcCBUxbRmoxoqKesAYngMNEvy11Wa63ENYu0QKAUIIPrlQWnwad3QAVBU/Z8VqBaDoQ2DadR4PK6D7b8S3b5SdD6AnX/XdKJb/zGpE904Jxr+QbTXWozCaGJwGcRnYHH92ZfjF8/fft/std7Rfs7LDJXlkhnTiaPCdl1ZK7jEOqClwYLxIzbAjoOKZWi61eT3a3jkmD64Zt1TFibs7xkVy4wZZYmLzJgdmou+hrzK1yltutqthCpKi4pPhdJSgs2hOSXoC43cypEDjGvhegU+ZJpx6w6uWUJ8ceTLYG8pjJfDpS23jVUytTnygDwkT0hMVsg6eUk2SZtw78T74H3yPvtv/I/+V//bNNT3znLuk3Pmn/4AGwYIbw==</latexit>
SCM with sigmoidal activation

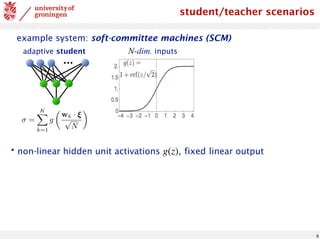
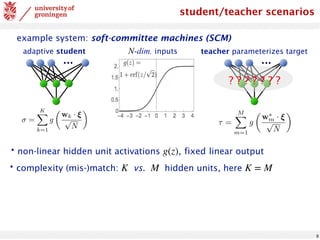
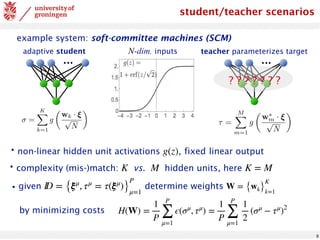
37. 10
simplification: orthonormal teacher vectors, isotropic input density
reflects permutation symmetry, allows for hidden unit specialization
Tij =
⇢
1 for i = j
0 else,
Rij =
⇢
R for i = j
S else,
Qij =
⇢
1 for i = j
C else.
<latexit
sha1_base64="z3U/1x66FQ8CCAKv5dCLWIcbiuE=">AAADPXicpVI7b9RAEF6bQBLzukBJMyICUSDLTiSSJlIgDWVel0S6PZ3We+O7TdZra3eNOFm+X5Ffk4aCf0BHR0PBQ4guLeu7gMhDCMRIK3365vHNzE5SSGFsFL33/Gsz12/Mzs0HN2/dvnO3tXBvz+Sl5tjmucz1QcIMSqGwbYWVeFBoZFkicT852mj8+69QG5GrXTsqsJuxgRKp4Mw6qrfg7ez2KnFYwxoAlZhaWgFNcCBUxbRmoxoqKesAYngMNEvy11Wa63ENYu0QKAUIIPrlQWnwad3QAVBU/Z8VqBaDoQ2DadR4PK6D7b8S3b5SdD6AnX/XdKJb/zGpE904Jxr+QbTXWozCaGJwGcRnYHH92ZfjF8/fft/std7Rfs7LDJXlkhnTiaPCdl1ZK7jEOqClwYLxIzbAjoOKZWi61eT3a3jkmD64Zt1TFibs7xkVy4wZZYmLzJgdmou+hrzK1yltutqthCpKi4pPhdJSgs2hOSXoC43cypEDjGvhegU+ZJpx6w6uWUJ8ceTLYG8pjJfDpS23jVUytTnygDwkT0hMVsg6eUk2SZtw78T74H3yPvtv/I/+V//bNNT3znLuk3Pmn/4AGwYIbw==</latexit>
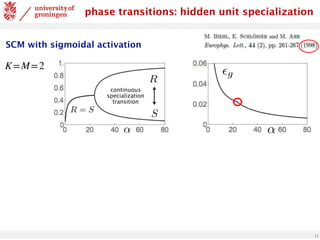
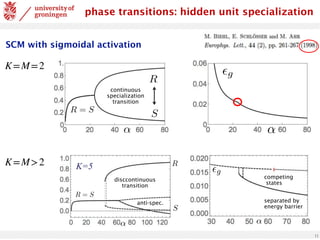
SCM with sigmoidal activation
✏g =
1
K
⇢
1
3
+
K 1
⇡

sin 1
✓
C
2
◆
2 sin 1
✓
S
2
◆
2
⇡
sin 1
✓
R
2
◆
<latexit
sha1_base64="050svsyqr1f80CEz0aVNkCq3F3g=">AAACx3icbVHLbtQwFHVSHiU8OpQlG4cKqQh1lKQSdIPUUhagbspj2krjMHI8zoyp85B9U3VkecE/8Ef8ATs2/AAbPgFPMkKlM1eyfHwesn1vVkuhIYp+ev7ajZu3bq/fCe7eu/9go/dw80RXjWJ8wCpZqbOMai5FyQcgQPKzWnFaZJKfZueHc/30gistqvITzGqeFnRSilwwCo4a9X4RXmshHZxgEr4iISa5oszE1hxZjInkORDzj9u1JHxOwqAjjki4Q0JHk1rY1jrERIvys9mJu/N2Zzy0JrFEickUnrUZnKz0fbzqa7c0wG2g05PFVauyH5ayxAaj3lbUj9rCyyBegK39F7+/vT74/ud41PtBxhVrCl4Ck1TrYRzVkBqqQDDJbUAazWvKzumEDx0sacF1ato5WPzUMWOcV8qtEnDLXk0YWmg9KzLnLChM9XVtTq7Shg3ke6kRZd0AL1l3Ud5IDBWeDxWPheIM5MwBypRwb8VsSl1XwI1+3oT4+peXwUnSj3f7yXvXjT3U1Tp6jJ6gbRSjl2gfvUXHaICY98b74mkP/Hd+5V/4l53V9xaZR+i/8r/+BbLn4Fo=</latexit>
=
⟨
1
2
(σ − τ)2
⟩
ξ
s =
1
2
ln det[ C ] (+ constant)
s =
1
2
ln
h
1+(K 1)C ((R S)+KS)
2
i
+K 1
2 ln
⇥
1 C (R S)2
⇤
<latexit
sha1_base64="R1D/dvB51gM9AtxPyLBvGiIN87s=">AAAC53icbZLLjtMwFIadcBvCrcCSjUtF1TKiSsKC2SCNNBukbgaGzoxUl8pxTlprHCfYDiKK+gJsWIAQW16JHS+DcC6gzgxHsvz7nN/57ONEueDa+P4vx71y9dr1Gzs3vVu379y917v/4FhnhWIwY5nI1GlENQguYWa4EXCaK6BpJOAkOjuo6ycfQGmeybemzGGR0pXkCWfU2NSy95tEsOKygveSKkXLpxtMBI1AVHpqpYGPRptSAPb08OUQk0RRVgWbKqx90g5IzBwHpL9L+qMp6T8j/WB80MxNbTR60yyOxo1lio+I4qu1Gb8LcasWmMhMFmkEChPiDfEQ7+Jqi9wyu2/XZIuOuc4FLTvDuYNYV8v/R7aovyyPgIy3LrvsDfyJ3wS+LIJODFAXh8veTxJnrEhBGiao1vPAz82iospwJmDjkUJDTtkZXcHcSklT0IuqeacNfmIzMU4yZYc0uMlu76hoqnWZRtaZUrPWF2t18n+1eWGSvUXFZV4YkKwFJYXAJsP1o+OYK2BGlFZQprg9K2Zrattq7K/h2SYEF698WRyHk+D5JHwdDvb3unbsoEfoMRqhAL1A++gVOkQzxJzY+eR8cb663P3sfnO/t1bX6fY8ROfC/fEHhtPgvQ==</latexit>
(+ constant)

38. 10
simplification: orthonormal teacher vectors, isotropic input density
reflects permutation symmetry, allows for hidden unit specialization
Tij =
⇢
1 for i = j
0 else,
Rij =
⇢
R for i = j
S else,
Qij =
⇢
1 for i = j
C else.
<latexit
sha1_base64="z3U/1x66FQ8CCAKv5dCLWIcbiuE=">AAADPXicpVI7b9RAEF6bQBLzukBJMyICUSDLTiSSJlIgDWVel0S6PZ3We+O7TdZra3eNOFm+X5Ffk4aCf0BHR0PBQ4guLeu7gMhDCMRIK3365vHNzE5SSGFsFL33/Gsz12/Mzs0HN2/dvnO3tXBvz+Sl5tjmucz1QcIMSqGwbYWVeFBoZFkicT852mj8+69QG5GrXTsqsJuxgRKp4Mw6qrfg7ez2KnFYwxoAlZhaWgFNcCBUxbRmoxoqKesAYngMNEvy11Wa63ENYu0QKAUIIPrlQWnwad3QAVBU/Z8VqBaDoQ2DadR4PK6D7b8S3b5SdD6AnX/XdKJb/zGpE904Jxr+QbTXWozCaGJwGcRnYHH92ZfjF8/fft/std7Rfs7LDJXlkhnTiaPCdl1ZK7jEOqClwYLxIzbAjoOKZWi61eT3a3jkmD64Zt1TFibs7xkVy4wZZYmLzJgdmou+hrzK1yltutqthCpKi4pPhdJSgs2hOSXoC43cypEDjGvhegU+ZJpx6w6uWUJ8ceTLYG8pjJfDpS23jVUytTnygDwkT0hMVsg6eUk2SZtw78T74H3yPvtv/I/+V//bNNT3znLuk3Pmn/4AGwYIbw==</latexit>
SCM with sigmoidal activation
✏g =
1
K
⇢
1
3
+
K 1
⇡

sin 1
✓
C
2
◆
2 sin 1
✓
S
2
◆
2
⇡
sin 1
✓
R
2
◆
<latexit
sha1_base64="050svsyqr1f80CEz0aVNkCq3F3g=">AAACx3icbVHLbtQwFHVSHiU8OpQlG4cKqQh1lKQSdIPUUhagbspj2krjMHI8zoyp85B9U3VkecE/8Ef8ATs2/AAbPgFPMkKlM1eyfHwesn1vVkuhIYp+ev7ajZu3bq/fCe7eu/9go/dw80RXjWJ8wCpZqbOMai5FyQcgQPKzWnFaZJKfZueHc/30gistqvITzGqeFnRSilwwCo4a9X4RXmshHZxgEr4iISa5oszE1hxZjInkORDzj9u1JHxOwqAjjki4Q0JHk1rY1jrERIvys9mJu/N2Zzy0JrFEickUnrUZnKz0fbzqa7c0wG2g05PFVauyH5ayxAaj3lbUj9rCyyBegK39F7+/vT74/ud41PtBxhVrCl4Ck1TrYRzVkBqqQDDJbUAazWvKzumEDx0sacF1ato5WPzUMWOcV8qtEnDLXk0YWmg9KzLnLChM9XVtTq7Shg3ke6kRZd0AL1l3Ud5IDBWeDxWPheIM5MwBypRwb8VsSl1XwI1+3oT4+peXwUnSj3f7yXvXjT3U1Tp6jJ6gbRSjl2gfvUXHaICY98b74mkP/Hd+5V/4l53V9xaZR+i/8r/+BbLn4Fo=</latexit>
=
⟨
1
2
(σ − τ)2
⟩
ξ
s =
1
2
ln det[ C ] (+ constant)
s =
1
2
ln
h
1+(K 1)C ((R S)+KS)
2
i
+K 1
2 ln
⇥
1 C (R S)2
⇤
<latexit
sha1_base64="R1D/dvB51gM9AtxPyLBvGiIN87s=">AAAC53icbZLLjtMwFIadcBvCrcCSjUtF1TKiSsKC2SCNNBukbgaGzoxUl8pxTlprHCfYDiKK+gJsWIAQW16JHS+DcC6gzgxHsvz7nN/57ONEueDa+P4vx71y9dr1Gzs3vVu379y917v/4FhnhWIwY5nI1GlENQguYWa4EXCaK6BpJOAkOjuo6ycfQGmeybemzGGR0pXkCWfU2NSy95tEsOKygveSKkXLpxtMBI1AVHpqpYGPRptSAPb08OUQk0RRVgWbKqx90g5IzBwHpL9L+qMp6T8j/WB80MxNbTR60yyOxo1lio+I4qu1Gb8LcasWmMhMFmkEChPiDfEQ7+Jqi9wyu2/XZIuOuc4FLTvDuYNYV8v/R7aovyyPgIy3LrvsDfyJ3wS+LIJODFAXh8veTxJnrEhBGiao1vPAz82iospwJmDjkUJDTtkZXcHcSklT0IuqeacNfmIzMU4yZYc0uMlu76hoqnWZRtaZUrPWF2t18n+1eWGSvUXFZV4YkKwFJYXAJsP1o+OYK2BGlFZQprg9K2Zrattq7K/h2SYEF698WRyHk+D5JHwdDvb3unbsoEfoMRqhAL1A++gVOkQzxJzY+eR8cb663P3sfnO/t1bX6fY8ROfC/fEHhtPgvQ==</latexit>
(+ constant)
David Saad, Sara Solla
Robert Urbanczik

39. 10
simplification: orthonormal teacher vectors, isotropic input density
reflects permutation symmetry, allows for hidden unit specialization
Tij =
⇢
1 for i = j
0 else,
Rij =
⇢
R for i = j
S else,
Qij =
⇢
1 for i = j
C else.
<latexit
sha1_base64="z3U/1x66FQ8CCAKv5dCLWIcbiuE=">AAADPXicpVI7b9RAEF6bQBLzukBJMyICUSDLTiSSJlIgDWVel0S6PZ3We+O7TdZra3eNOFm+X5Ffk4aCf0BHR0PBQ4guLeu7gMhDCMRIK3365vHNzE5SSGFsFL33/Gsz12/Mzs0HN2/dvnO3tXBvz+Sl5tjmucz1QcIMSqGwbYWVeFBoZFkicT852mj8+69QG5GrXTsqsJuxgRKp4Mw6qrfg7ez2KnFYwxoAlZhaWgFNcCBUxbRmoxoqKesAYngMNEvy11Wa63ENYu0QKAUIIPrlQWnwad3QAVBU/Z8VqBaDoQ2DadR4PK6D7b8S3b5SdD6AnX/XdKJb/zGpE904Jxr+QbTXWozCaGJwGcRnYHH92ZfjF8/fft/std7Rfs7LDJXlkhnTiaPCdl1ZK7jEOqClwYLxIzbAjoOKZWi61eT3a3jkmD64Zt1TFibs7xkVy4wZZYmLzJgdmou+hrzK1yltutqthCpKi4pPhdJSgs2hOSXoC43cypEDjGvhegU+ZJpx6w6uWUJ8ceTLYG8pjJfDpS23jVUytTnygDwkT0hMVsg6eUk2SZtw78T74H3yPvtv/I/+V//bNNT3znLuk3Pmn/4AGwYIbw==</latexit>
SCM with sigmoidal activation
✏g =
1
K
⇢
1
3
+
K 1
⇡

sin 1
✓
C
2
◆
2 sin 1
✓
S
2
◆
2
⇡
sin 1
✓
R
2
◆
<latexit
sha1_base64="050svsyqr1f80CEz0aVNkCq3F3g=">AAACx3icbVHLbtQwFHVSHiU8OpQlG4cKqQh1lKQSdIPUUhagbspj2krjMHI8zoyp85B9U3VkecE/8Ef8ATs2/AAbPgFPMkKlM1eyfHwesn1vVkuhIYp+ev7ajZu3bq/fCe7eu/9go/dw80RXjWJ8wCpZqbOMai5FyQcgQPKzWnFaZJKfZueHc/30gistqvITzGqeFnRSilwwCo4a9X4RXmshHZxgEr4iISa5oszE1hxZjInkORDzj9u1JHxOwqAjjki4Q0JHk1rY1jrERIvys9mJu/N2Zzy0JrFEickUnrUZnKz0fbzqa7c0wG2g05PFVauyH5ayxAaj3lbUj9rCyyBegK39F7+/vT74/ud41PtBxhVrCl4Ck1TrYRzVkBqqQDDJbUAazWvKzumEDx0sacF1ato5WPzUMWOcV8qtEnDLXk0YWmg9KzLnLChM9XVtTq7Shg3ke6kRZd0AL1l3Ud5IDBWeDxWPheIM5MwBypRwb8VsSl1XwI1+3oT4+peXwUnSj3f7yXvXjT3U1Tp6jJ6gbRSjl2gfvUXHaICY98b74mkP/Hd+5V/4l53V9xaZR+i/8r/+BbLn4Fo=</latexit>
=
⟨
1
2
(σ − τ)2
⟩
ξ
s =
1
2
ln det[ C ] (+ constant)
s =
1
2
ln
h
1+(K 1)C ((R S)+KS)
2
i
+K 1
2 ln
⇥
1 C (R S)2
⇤
<latexit
sha1_base64="R1D/dvB51gM9AtxPyLBvGiIN87s=">AAAC53icbZLLjtMwFIadcBvCrcCSjUtF1TKiSsKC2SCNNBukbgaGzoxUl8pxTlprHCfYDiKK+gJsWIAQW16JHS+DcC6gzgxHsvz7nN/57ONEueDa+P4vx71y9dr1Gzs3vVu379y917v/4FhnhWIwY5nI1GlENQguYWa4EXCaK6BpJOAkOjuo6ycfQGmeybemzGGR0pXkCWfU2NSy95tEsOKygveSKkXLpxtMBI1AVHpqpYGPRptSAPb08OUQk0RRVgWbKqx90g5IzBwHpL9L+qMp6T8j/WB80MxNbTR60yyOxo1lio+I4qu1Gb8LcasWmMhMFmkEChPiDfEQ7+Jqi9wyu2/XZIuOuc4FLTvDuYNYV8v/R7aovyyPgIy3LrvsDfyJ3wS+LIJODFAXh8veTxJnrEhBGiao1vPAz82iospwJmDjkUJDTtkZXcHcSklT0IuqeacNfmIzMU4yZYc0uMlu76hoqnWZRtaZUrPWF2t18n+1eWGSvUXFZV4YkKwFJYXAJsP1o+OYK2BGlFZQprg9K2Zrattq7K/h2SYEF698WRyHk+D5JHwdDvb3unbsoEfoMRqhAL1A++gVOkQzxJzY+eR8cb663P3sfnO/t1bX6fY8ROfC/fEHhtPgvQ==</latexit>
(+ constant)
minimize (βf ) = α ϵg − s(ϵg) →
R(α)
C(α)
S(α)
→ ϵg(α)
success of learning
as a function of
the training set size
David Saad, Sara Solla
Robert Urbanczik

40. 11
↵
<
latexit
sha1_base64="+wSBPeL8nxBdvzPXA2qswhGhfpg=">AAAB7XicbVBNS8NAEJ3Ur1q/qh69LBbBU0mqoMeiF48V7Ae0oUy2m3btZhN2N0IJ/Q9ePCji1f/jzX/jts1BWx8MPN6bYWZekAiujet+O4W19Y3NreJ2aWd3b/+gfHjU0nGqKGvSWMSqE6BmgkvWNNwI1kkUwygQrB2Mb2d++4kpzWP5YCYJ8yMcSh5yisZKrR6KZIT9csWtunOQVeLlpAI5Gv3yV28Q0zRi0lCBWnc9NzF+hspwKti01Es1S5COcci6lkqMmPaz+bVTcmaVAQljZUsaMld/T2QYaT2JAtsZoRnpZW8m/ud1UxNe+xmXSWqYpItFYSqIicnsdTLgilEjJpYgVdzeSugIFVJjAyrZELzll1dJq1b1Lqq1+8tK/SaPowgncArn4MEV1OEOGtAECo/wDK/w5sTOi/PufCxaC04+cwx/4Hz+AIzPjxw=</latexit>
R
<
latexit
sha1_base64="cVRUNBy/RTcU6LUbsjbBwonoaeo=">AAAB6HicbVDLTgJBEOzFF+IL9ehlIjHxRHbRRI9ELx7ByCOBDZkdemFkdnYzM2tCCF/gxYPGePWTvPk3DrAHBSvppFLVne6uIBFcG9f9dnJr6xubW/ntws7u3v5B8fCoqeNUMWywWMSqHVCNgktsGG4EthOFNAoEtoLR7cxvPaHSPJYPZpygH9GB5CFn1Fipft8rltyyOwdZJV5GSpCh1it+dfsxSyOUhgmqdcdzE+NPqDKcCZwWuqnGhLIRHWDHUkkj1P5kfuiUnFmlT8JY2ZKGzNXfExMaaT2OAtsZUTPUy95M/M/rpCa89idcJqlByRaLwlQQE5PZ16TPFTIjxpZQpri9lbAhVZQZm03BhuAtv7xKmpWyd1Gu1C9L1ZssjjycwCmcgwdXUIU7qEEDGCA8wyu8OY/Oi/PufCxac042cwx/4Hz+AK3vjNo=</latexit>
S
<
latexit
sha1_base64="vFchJGr6Z+gyWiveB04FdIL/myI=">AAAB6HicbVDLTgJBEOzFF+IL9ehlIjHxRHbRRI9ELx4hyiOBDZkdemFkdnYzM2tCCF/gxYPGePWTvPk3DrAHBSvppFLVne6uIBFcG9f9dnJr6xubW/ntws7u3v5B8fCoqeNUMWywWMSqHVCNgktsGG4EthOFNAoEtoLR7cxvPaHSPJYPZpygH9GB5CFn1Fipft8rltyyOwdZJV5GSpCh1it+dfsxSyOUhgmqdcdzE+NPqDKcCZwWuqnGhLIRHWDHUkkj1P5kfuiUnFmlT8JY2ZKGzNXfExMaaT2OAtsZUTPUy95M/M/rpCa89idcJqlByRaLwlQQE5PZ16TPFTIjxpZQpri9lbAhVZQZm03BhuAtv7xKmpWyd1Gu1C9L1ZssjjycwCmcgwdXUIU7qEEDGCA8wyu8OY/Oi/PufCxac042cwx/4Hz+AK9zjNs=</latexit>
R = S
<latexit
sha1_base64="nDUP4fccke/FNLKaaM8Wqz9O1M8=">AAAB6nicbVDLSgNBEOz1GeMr6tHLYBA8hd0o6EUIevEYjXlAsoTZSW8yZHZ2mZkVQsgnePGgiFe/yJt/4yTZgyYWNBRV3XR3BYng2rjut7Oyura+sZnbym/v7O7tFw4OGzpOFcM6i0WsWgHVKLjEuuFGYCtRSKNAYDMY3k795hMqzWP5aEYJ+hHtSx5yRo2Vag/XtW6h6JbcGcgy8TJShAzVbuGr04tZGqE0TFCt256bGH9MleFM4CTfSTUmlA1pH9uWShqh9sezUyfk1Co9EsbKljRkpv6eGNNI61EU2M6ImoFe9Kbif147NeGVP+YySQ1KNl8UpoKYmEz/Jj2ukBkxsoQyxe2thA2ooszYdPI2BG/x5WXSKJe881L5/qJYucniyMExnMAZeHAJFbiDKtSBQR+e4RXeHOG8OO/Ox7x1xclmjuAPnM8f0umNfg==</latexit>
✏g
<latexit
sha1_base64="mglHXcqwu+eocCx6ul5cTySUvNg=">AAAB8XicbVBNS8NAEJ3Ur1q/qh69LBbBU0mqoMeiF48V7Ae2oWy2k3bpZhN2N0IJ/RdePCji1X/jzX/jts1BWx8MPN6bYWZekAiujet+O4W19Y3NreJ2aWd3b/+gfHjU0nGqGDZZLGLVCahGwSU2DTcCO4lCGgUC28H4dua3n1BpHssHM0nQj+hQ8pAzaqz02MNEcxHL/rBfrrhVdw6ySrycVCBHo1/+6g1ilkYoDRNU667nJsbPqDKcCZyWeqnGhLIxHWLXUkkj1H42v3hKzqwyIGGsbElD5urviYxGWk+iwHZG1Iz0sjcT//O6qQmv/YzLJDUo2WJRmApiYjJ7nwy4QmbExBLKFLe3EjaiijJjQyrZELzll1dJq1b1Lqq1+8tK/SaPowgncArn4MEV1OEOGtAEBhKe4RXeHO28OO/Ox6K14OQzx/AHzucPyzeQ/g==</latexit>
↵
<
latexit
sha1_base64="+wSBPeL8nxBdvzPXA2qswhGhfpg=">AAAB7XicbVBNS8NAEJ3Ur1q/qh69LBbBU0mqoMeiF48V7Ae0oUy2m3btZhN2N0IJ/Q9ePCji1f/jzX/jts1BWx8MPN6bYWZekAiujet+O4W19Y3NreJ2aWd3b/+gfHjU0nGqKGvSWMSqE6BmgkvWNNwI1kkUwygQrB2Mb2d++4kpzWP5YCYJ8yMcSh5yisZKrR6KZIT9csWtunOQVeLlpAI5Gv3yV28Q0zRi0lCBWnc9NzF+hspwKti01Es1S5COcci6lkqMmPaz+bVTcmaVAQljZUsaMld/T2QYaT2JAtsZoRnpZW8m/ud1UxNe+xmXSWqYpItFYSqIicnsdTLgilEjJpYgVdzeSugIFVJjAyrZELzll1dJq1b1Lqq1+8tK/SaPowgncArn4MEV1OEOGtAECo/wDK/w5sTOi/PufCxaC04+cwx/4Hz+AIzPjxw=</latexit>
K=M=2
phase transitions: hidden unit specialization
SCM with sigmoidal activation
continuous
specialization
transition

41. 11
↵
<
latexit
sha1_base64="+wSBPeL8nxBdvzPXA2qswhGhfpg=">AAAB7XicbVBNS8NAEJ3Ur1q/qh69LBbBU0mqoMeiF48V7Ae0oUy2m3btZhN2N0IJ/Q9ePCji1f/jzX/jts1BWx8MPN6bYWZekAiujet+O4W19Y3NreJ2aWd3b/+gfHjU0nGqKGvSWMSqE6BmgkvWNNwI1kkUwygQrB2Mb2d++4kpzWP5YCYJ8yMcSh5yisZKrR6KZIT9csWtunOQVeLlpAI5Gv3yV28Q0zRi0lCBWnc9NzF+hspwKti01Es1S5COcci6lkqMmPaz+bVTcmaVAQljZUsaMld/T2QYaT2JAtsZoRnpZW8m/ud1UxNe+xmXSWqYpItFYSqIicnsdTLgilEjJpYgVdzeSugIFVJjAyrZELzll1dJq1b1Lqq1+8tK/SaPowgncArn4MEV1OEOGtAECo/wDK/w5sTOi/PufCxaC04+cwx/4Hz+AIzPjxw=</latexit>
R
<
latexit
sha1_base64="cVRUNBy/RTcU6LUbsjbBwonoaeo=">AAAB6HicbVDLTgJBEOzFF+IL9ehlIjHxRHbRRI9ELx7ByCOBDZkdemFkdnYzM2tCCF/gxYPGePWTvPk3DrAHBSvppFLVne6uIBFcG9f9dnJr6xubW/ntws7u3v5B8fCoqeNUMWywWMSqHVCNgktsGG4EthOFNAoEtoLR7cxvPaHSPJYPZpygH9GB5CFn1Fipft8rltyyOwdZJV5GSpCh1it+dfsxSyOUhgmqdcdzE+NPqDKcCZwWuqnGhLIRHWDHUkkj1P5kfuiUnFmlT8JY2ZKGzNXfExMaaT2OAtsZUTPUy95M/M/rpCa89idcJqlByRaLwlQQE5PZ16TPFTIjxpZQpri9lbAhVZQZm03BhuAtv7xKmpWyd1Gu1C9L1ZssjjycwCmcgwdXUIU7qEEDGCA8wyu8OY/Oi/PufCxac042cwx/4Hz+AK3vjNo=</latexit>
S
<
latexit
sha1_base64="vFchJGr6Z+gyWiveB04FdIL/myI=">AAAB6HicbVDLTgJBEOzFF+IL9ehlIjHxRHbRRI9ELx4hyiOBDZkdemFkdnYzM2tCCF/gxYPGePWTvPk3DrAHBSvppFLVne6uIBFcG9f9dnJr6xubW/ntws7u3v5B8fCoqeNUMWywWMSqHVCNgktsGG4EthOFNAoEtoLR7cxvPaHSPJYPZpygH9GB5CFn1Fipft8rltyyOwdZJV5GSpCh1it+dfsxSyOUhgmqdcdzE+NPqDKcCZwWuqnGhLIRHWDHUkkj1P5kfuiUnFmlT8JY2ZKGzNXfExMaaT2OAtsZUTPUy95M/M/rpCa89idcJqlByRaLwlQQE5PZ16TPFTIjxpZQpri9lbAhVZQZm03BhuAtv7xKmpWyd1Gu1C9L1ZssjjycwCmcgwdXUIU7qEEDGCA8wyu8OY/Oi/PufCxac042cwx/4Hz+AK9zjNs=</latexit>
R = S
<latexit
sha1_base64="nDUP4fccke/FNLKaaM8Wqz9O1M8=">AAAB6nicbVDLSgNBEOz1GeMr6tHLYBA8hd0o6EUIevEYjXlAsoTZSW8yZHZ2mZkVQsgnePGgiFe/yJt/4yTZgyYWNBRV3XR3BYng2rjut7Oyura+sZnbym/v7O7tFw4OGzpOFcM6i0WsWgHVKLjEuuFGYCtRSKNAYDMY3k795hMqzWP5aEYJ+hHtSx5yRo2Vag/XtW6h6JbcGcgy8TJShAzVbuGr04tZGqE0TFCt256bGH9MleFM4CTfSTUmlA1pH9uWShqh9sezUyfk1Co9EsbKljRkpv6eGNNI61EU2M6ImoFe9Kbif147NeGVP+YySQ1KNl8UpoKYmEz/Jj2ukBkxsoQyxe2thA2ooszYdPI2BG/x5WXSKJe881L5/qJYucniyMExnMAZeHAJFbiDKtSBQR+e4RXeHOG8OO/Ox7x1xclmjuAPnM8f0umNfg==</latexit>
✏g
<latexit
sha1_base64="mglHXcqwu+eocCx6ul5cTySUvNg=">AAAB8XicbVBNS8NAEJ3Ur1q/qh69LBbBU0mqoMeiF48V7Ae2oWy2k3bpZhN2N0IJ/RdePCji1X/jzX/jts1BWx8MPN6bYWZekAiujet+O4W19Y3NreJ2aWd3b/+gfHjU0nGqGDZZLGLVCahGwSU2DTcCO4lCGgUC28H4dua3n1BpHssHM0nQj+hQ8pAzaqz02MNEcxHL/rBfrrhVdw6ySrycVCBHo1/+6g1ilkYoDRNU667nJsbPqDKcCZyWeqnGhLIxHWLXUkkj1H42v3hKzqwyIGGsbElD5urviYxGWk+iwHZG1Iz0sjcT//O6qQmv/YzLJDUo2WJRmApiYjJ7nwy4QmbExBLKFLe3EjaiijJjQyrZELzll1dJq1b1Lqq1+8tK/SaPowgncArn4MEV1OEOGtAEBhKe4RXeHO28OO/Ox6K14OQzx/AHzucPyzeQ/g==</latexit>
↵
<
latexit
sha1_base64="+wSBPeL8nxBdvzPXA2qswhGhfpg=">AAAB7XicbVBNS8NAEJ3Ur1q/qh69LBbBU0mqoMeiF48V7Ae0oUy2m3btZhN2N0IJ/Q9ePCji1f/jzX/jts1BWx8MPN6bYWZekAiujet+O4W19Y3NreJ2aWd3b/+gfHjU0nGqKGvSWMSqE6BmgkvWNNwI1kkUwygQrB2Mb2d++4kpzWP5YCYJ8yMcSh5yisZKrR6KZIT9csWtunOQVeLlpAI5Gv3yV28Q0zRi0lCBWnc9NzF+hspwKti01Es1S5COcci6lkqMmPaz+bVTcmaVAQljZUsaMld/T2QYaT2JAtsZoRnpZW8m/ud1UxNe+xmXSWqYpItFYSqIicnsdTLgilEjJpYgVdzeSugIFVJjAyrZELzll1dJq1b1Lqq1+8tK/SaPowgncArn4MEV1OEOGtAECo/wDK/w5sTOi/PufCxaC04+cwx/4Hz+AIzPjxw=</latexit>
K=M=2
phase transitions: hidden unit specialization
SCM with sigmoidal activation
↵
<
latexit
sha1_base64="+wSBPeL8nxBdvzPXA2qswhGhfpg=">AAAB7XicbVBNS8NAEJ3Ur1q/qh69LBbBU0mqoMeiF48V7Ae0oUy2m3btZhN2N0IJ/Q9ePCji1f/jzX/jts1BWx8MPN6bYWZekAiujet+O4W19Y3NreJ2aWd3b/+gfHjU0nGqKGvSWMSqE6BmgkvWNNwI1kkUwygQrB2Mb2d++4kpzWP5YCYJ8yMcSh5yisZKrR6KZIT9csWtunOQVeLlpAI5Gv3yV28Q0zRi0lCBWnc9NzF+hspwKti01Es1S5COcci6lkqMmPaz+bVTcmaVAQljZUsaMld/T2QYaT2JAtsZoRnpZW8m/ud1UxNe+xmXSWqYpItFYSqIicnsdTLgilEjJpYgVdzeSugIFVJjAyrZELzll1dJq1b1Lqq1+8tK/SaPowgncArn4MEV1OEOGtAECo/wDK/w5sTOi/PufCxaC04+cwx/4Hz+AIzPjxw=</latexit>
R
<
latexit
sha1_base64="cVRUNBy/RTcU6LUbsjbBwonoaeo=">AAAB6HicbVDLTgJBEOzFF+IL9ehlIjHxRHbRRI9ELx7ByCOBDZkdemFkdnYzM2tCCF/gxYPGePWTvPk3DrAHBSvppFLVne6uIBFcG9f9dnJr6xubW/ntws7u3v5B8fCoqeNUMWywWMSqHVCNgktsGG4EthOFNAoEtoLR7cxvPaHSPJYPZpygH9GB5CFn1Fipft8rltyyOwdZJV5GSpCh1it+dfsxSyOUhgmqdcdzE+NPqDKcCZwWuqnGhLIRHWDHUkkj1P5kfuiUnFmlT8JY2ZKGzNXfExMaaT2OAtsZUTPUy95M/M/rpCa89idcJqlByRaLwlQQE5PZ16TPFTIjxpZQpri9lbAhVZQZm03BhuAtv7xKmpWyd1Gu1C9L1ZssjjycwCmcgwdXUIU7qEEDGCA8wyu8OY/Oi/PufCxac042cwx/4Hz+AK3vjNo=</latexit>
S
<
latexit
sha1_base64="vFchJGr6Z+gyWiveB04FdIL/myI=">AAAB6HicbVDLTgJBEOzFF+IL9ehlIjHxRHbRRI9ELx4hyiOBDZkdemFkdnYzM2tCCF/gxYPGePWTvPk3DrAHBSvppFLVne6uIBFcG9f9dnJr6xubW/ntws7u3v5B8fCoqeNUMWywWMSqHVCNgktsGG4EthOFNAoEtoLR7cxvPaHSPJYPZpygH9GB5CFn1Fipft8rltyyOwdZJV5GSpCh1it+dfsxSyOUhgmqdcdzE+NPqDKcCZwWuqnGhLIRHWDHUkkj1P5kfuiUnFmlT8JY2ZKGzNXfExMaaT2OAtsZUTPUy95M/M/rpCa89idcJqlByRaLwlQQE5PZ16TPFTIjxpZQpri9lbAhVZQZm03BhuAtv7xKmpWyd1Gu1C9L1ZssjjycwCmcgwdXUIU7qEEDGCA8wyu8OY/Oi/PufCxac042cwx/4Hz+AK9zjNs=</latexit>
R = S
<latexit
sha1_base64="nDUP4fccke/FNLKaaM8Wqz9O1M8=">AAAB6nicbVDLSgNBEOz1GeMr6tHLYBA8hd0o6EUIevEYjXlAsoTZSW8yZHZ2mZkVQsgnePGgiFe/yJt/4yTZgyYWNBRV3XR3BYng2rjut7Oyura+sZnbym/v7O7tFw4OGzpOFcM6i0WsWgHVKLjEuuFGYCtRSKNAYDMY3k795hMqzWP5aEYJ+hHtSx5yRo2Vag/XtW6h6JbcGcgy8TJShAzVbuGr04tZGqE0TFCt256bGH9MleFM4CTfSTUmlA1pH9uWShqh9sezUyfk1Co9EsbKljRkpv6eGNNI61EU2M6ImoFe9Kbif147NeGVP+YySQ1KNl8UpoKYmEz/Jj2ukBkxsoQyxe2thA2ooszYdPI2BG/x5WXSKJe881L5/qJYucniyMExnMAZeHAJFbiDKtSBQR+e4RXeHOG8OO/Ox7x1xclmjuAPnM8f0umNfg==</latexit>
K=M>2 K=5 ✏g
<latexit
sha1_base64="mglHXcqwu+eocCx6ul5cTySUvNg=">AAAB8XicbVBNS8NAEJ3Ur1q/qh69LBbBU0mqoMeiF48V7Ae2oWy2k3bpZhN2N0IJ/RdePCji1X/jzX/jts1BWx8MPN6bYWZekAiujet+O4W19Y3NreJ2aWd3b/+gfHjU0nGqGDZZLGLVCahGwSU2DTcCO4lCGgUC28H4dua3n1BpHssHM0nQj+hQ8pAzaqz02MNEcxHL/rBfrrhVdw6ySrycVCBHo1/+6g1ilkYoDRNU667nJsbPqDKcCZyWeqnGhLIxHWLXUkkj1H42v3hKzqwyIGGsbElD5urviYxGWk+iwHZG1Iz0sjcT//O6qQmv/YzLJDUo2WJRmApiYjJ7nwy4QmbExBLKFLe3EjaiijJjQyrZELzll1dJq1b1Lqq1+8tK/SaPowgncArn4MEV1OEOGtAEBhKe4RXeHO28OO/Ox6K14OQzx/AHzucPyzeQ/g==</latexit>
↵
<
latexit
sha1_base64="+wSBPeL8nxBdvzPXA2qswhGhfpg=">AAAB7XicbVBNS8NAEJ3Ur1q/qh69LBbBU0mqoMeiF48V7Ae0oUy2m3btZhN2N0IJ/Q9ePCji1f/jzX/jts1BWx8MPN6bYWZekAiujet+O4W19Y3NreJ2aWd3b/+gfHjU0nGqKGvSWMSqE6BmgkvWNNwI1kkUwygQrB2Mb2d++4kpzWP5YCYJ8yMcSh5yisZKrR6KZIT9csWtunOQVeLlpAI5Gv3yV28Q0zRi0lCBWnc9NzF+hspwKti01Es1S5COcci6lkqMmPaz+bVTcmaVAQljZUsaMld/T2QYaT2JAtsZoRnpZW8m/ud1UxNe+xmXSWqYpItFYSqIicnsdTLgilEjJpYgVdzeSugIFVJjAyrZELzll1dJq1b1Lqq1+8tK/SaPowgncArn4MEV1OEOGtAECo/wDK/w5sTOi/PufCxaC04+cwx/4Hz+AIzPjxw=</latexit>
competing
states
separated by
energy barrier
continuous
specialization
transition
disccontinuous
transition
anti-spec.

42. 12
Hidden unit Specialization in Layered Neural Networks:
ReLU vs. Sigmoidal Activation
Elisa Oostwal, Michiel Straat, M. Biehl
Physica A 564: 125517 (2021)
Phase Transitions in Soft-Committee Machines
M. Biehl, E. Schlösser, M. Ahr
Europhysics Letters 44: 261-267 (1998)
Statistical Physics and Practical Training of Soft-Committee Machines
M. Ahr, M. Biehl, R. Urbanczik
European Physics B 10: 583-588 (1999)
sigmoidal activation
high-T, arbitrary K = M
sigmoidal activation,
replica, large
T < ∞
K = M → ∞
ReLU activation
high-T, arbitrary K = M
references

43. 13
challenges:
- more general activation functions,
see the following talk by Frederieke Richert
- overfitting/underfitting (mismatched students)
- low temperature training (Annealed Approximation, Replica)
outlook

44. 13
challenges:
- more general activation functions,
see the following talk by Frederieke Richert
- overfitting/underfitting (mismatched students)
- low temperature training (Annealed Approximation, Replica)
- many layers (deep networks, tree architectures)
- realistic input densities
- material specific activation functions
- regularization techniques, e.g. drop-out
-
outlook

45. 14
Cognigron March 2021 12 / 11
www.cs.rug.nl/~biehl m.biehl@rug.nl