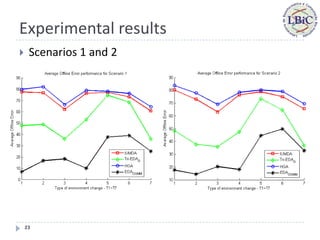
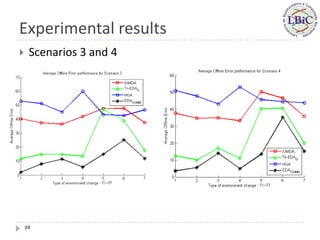
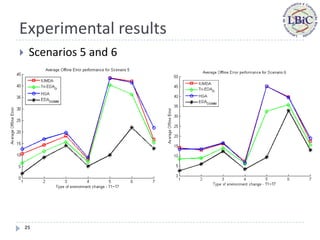
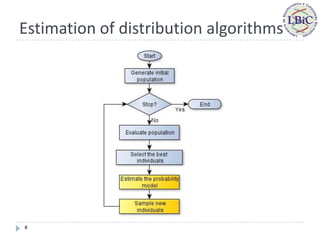
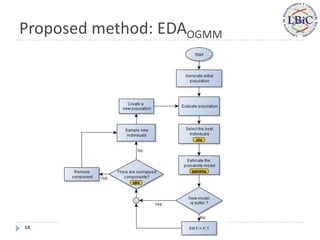
This document proposes a new estimation of distribution algorithm called EDAOGMM that uses an online Gaussian mixture model to optimize problems in dynamic environments. EDAOGMM adapts its internal model through online learning as the environment changes. It was tested on benchmark dynamic optimization problems and outperformed other state-of-the-art algorithms, especially in high-frequency changing environments. Future work includes improving EDAOGMM's ability to avoid premature convergence and further experimental testing.

1. Departamento de Engenharia de Faculdade de Engenharia Unicamp
Computação e Automação Elétrica e de Computação
Industrial
Online learning in estimation of distribution
algorithms for dynamic environments
André Ricardo Gonçalves
Fernando J. Von Zuben

2. Outline
 Optimization in dynamic environments
 Estimation of distribution algorithms
 Mixture model and online learning
 Proposed method: EDAOGMM
 Experimental results
 Concluding remarks and future works
 References
2

3. Outline
 Optimization in dynamic environments
 Estimation of distribution algorithms
 Mixture model and online learning
 Proposed method: EDAOGMM
 Experimental results
 Concluding remarks and future works
 References
3

4. Optimization in dynamic environments
 World is dynamic!
 New events arrive and others canceled at a scheduling
problem;
 Vehicles must reroute around heavy trac and road repairs;
 Machine breakdown occurs during a production run.
4

5. Optimization in dynamic environments
 Dynamic optimization algorithm should be able to react to the
new environment, updating the internal model and generating
new candidate solutions;
 Evolutionary algorithms (EAs) appear as promising
approaches, since they maintain a population of solutions that
can be adapted by means of a balance between exploration
and exploitation of the search space;
 EAs approaches: GA, PSO, AIS, EDAs, among others;
 However, to be applied in dynamic environments, they must
be adapted.
5

6. Outline
 Optimization in dynamic environments
 Estimation of distribution algorithms
 Mixture model and online learning
 Proposed method: EDAOGMM
 Experimental results
 Concluding remarks and future works
 References
6

7. Estimation of distribution algorithms
 Estimation of distribution algorithms (EDA) are
evolutionary methods that use estimation of
distribution techniques, instead of genetic operators.
 The key aspect in EDAs is how to estimate the true
distribution of promising solutions.
 Dependence trees, Bayesian networks, mixture models, etc.
 Classication of EDAs based on complexity of
probabilistic model.
7

8. Estimation of distribution algorithms
8

9. Outline
 Optimization in dynamic environments
 Estimation of distribution algorithms
 Mixture model and online learning
 Proposed method: EDAOGMM
 Experimental results
 Concluding remarks and future works
 References
9

10. Mixture model and online learning
 Mixture models are flexible estimators;
 In optimization, they are able to capture the
multimodality of the search space;
 Learning methods, such as Expectation-Maximization
(EM), are computationally efficient;
 In optimization of dynamic environments, the model
tends to change constantly;
 EM with online learning appear as a promising approach
to model dynamic environments.
10

11. Mixture model and online learning
 Online learning
 Fast adaptation model to the new data coming from the
environment;
 Approach proposed by (Nowlan,1991) stores the relevant
information in a vector of sufficient statistics;
 Exponential decay (γ) of the data importance to the model.
11

12. Outline
 Optimization in dynamic environments
 Estimation of distribution algorithms
 Mixture model and online learning
 Proposed method: EDAOGMM
 Experimental results
 Concluding remarks and future works
 References
12

13. Proposed method: EDAOGMM
 EDA with online Gaussian mixture model (EDAOGMM)
 Employs an incremental and constructive mixture model (low
computational cost);
 Self-adjusts the components number by means of BIC;
 Model tends to adapt to the multimodality of search space;
 Employs a “random immigrants” approach to promote
population diversity;
13

14. Proposed method: EDAOGMM
14

15. Proposed method: EDAOGMM
 Selection method:
 Stochastic selection aids to preserve the population diversity;
 η parameter defines the balance between exploration and
explotation.
 Diversity control:
 Stochastic selection;
 Random immigrants;
 Controlled reinitializations (δ parameter).
 Components number control:
 Incremental and constructive approach;
 Removal of overlapped components (ε parameter).
15

16. Proposed method: EDAOGMM
 New population is composed by 3 subpopulations (dependent
of the η parameter):
 Sampled by the mixture model;
 Best individuals;
 Random immigrants.
 Overlapped components is a redundant representation of a
promising region
 Remove the component with lower mixture coefficient;
 Check the overlap using the ε parameter.
16

17. Outline
 Optimization in dynamic environments
 Estimation of distribution algorithms
 Mixture model and online learning
 Proposed method: EDAOGMM
 Experimental results
 Concluding remarks and future works
 References
17

18. Experimental results
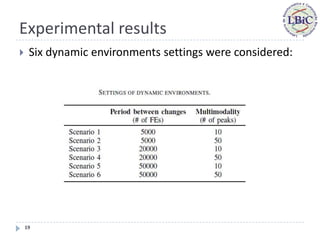
 Moving Peaks benchmark (MPB) generator plus a rotation method
(Li & Yang, 2008);
 Fitness surface are composed by a set of peaks that changes your
positions, heights and widths over time;
 Maximization problem in a continuous space;
 Seven types of change (T1-T7): small step, large step, random,
chaotic, recurrent, recurrent with noise and random with
dimensional changes;
 There are parameters to control the multimodality of the search
space, severity of changes and the dynamism of the environment;
 Range of search space: [-5,5];
 Problem dimensions: 10 and [5-15].
18

19. Experimental results
 Six dynamic environments settings were considered:
19

20. Experimental results
 Contenders proposed algorithms in the literature:
 Improved Univariate Marginal Distribution Algorithm -
IUMDA (Liu et al., 2008);
 Tri-EDAG (Yuan et al., 2008);
 Hypermutation Genetic Algorithm - HGA (Cobb,1990).
 Two EDAs and a GA developed for dynamic
environments.
20

21. Experimental results
 Free parameters settings:
21

22. Experimental results
 Comparison metrics:
 Offline error
 Average of the absolute error between the best solution found
so far and the global optimum (known) at each time step t.
22

23. Experimental results
 Scenarios 1 and 2
23

24. Experimental results
 Scenarios 3 and 4
24

25. Experimental results
 Scenarios 5 and 6
25

26. Outline
 Optimization in dynamic environments
 Estimation of distribution algorithms
 Mixture model and online learning
 Proposed method: EDAOGMM
 Experimental results
 Concluding remarks and future works
 References
26

27. Concluding remarks and future works
 EDAOGMM outperforms all the contenders, particularly in
high-frequency changing environments (Scenarios 1 and 2);
 EDAOGMM has a fast convergence because it can explore
several peaks simultaneously;
 We can detect a less prominent performance in low
frequency scenarios (5 and 6), indicating that, once
converged, the EDAOGMM reduces its exploration power;
 So, a continued control to avoid premature convergence is
desirable.
27

28. Concluding remarks and future works
 Future works:
 Incorporate a continued convergence control mechanism;
 Compare EDAOGMM with other algorithms designed to deal
with dynamic environments;
 Increment the experimental tests aiming at investigating
scalability and other aspects related to the relative
performance of the proposed algorithm;
 Performs a parameter sensitivity analisys.
28

29. Outline
 Optimization in dynamic environments
 Estimation of distribution algorithms
 Mixture model and online learning
 Proposed method: EDAOGMM
 Experimental results
 Concluding remarks and future works
 References
29

30. References
 S. Nowlan, “Soft competitive adaptation: neural network learning
algorithms based on fitting statistical mixtures,” Ph.D. dissertation,
Carnegie Mellon University, Pittsburgh, PA, USA, 1991.
 C. Li and S. Yang, “A generalized approach to construct benchmark
problems for dynamic optimization,” in Proc. of the 7th Int. Conf. on
Simulated Evolution and Learning, 2008.
 X. Liu, Y. Wu, and J. Ye, “An Improved Estimation of Distribution Algorithmin
Dynamic Environments,” in Fourth International Conference on Natural
Computation. IEEE Computer Society, 2008, pp. 269–272.
 B. Yuan, M. Orlowska, and S. Sadiq, “Extending a class of continuous
estimation of distribution algorithms to dynamic problems,” Optimization
Letters, vol. 2, no. 3, pp. 433–443, 2008.
 H. Cobb, “An investigation into the use of hypermutation as an adaptive
operator in genetic algorithms having continuous, time-dependent
nonstationary environments,” Naval Research Laboratory, Tech. Rep., 1990.
30

31. Departamento de Engenharia de Faculdade de Engenharia Unicamp
Computação e Automação Elétrica e de Computação
Industrial
Online learning in estimation of distribution
algorithms for dynamic environments
André Ricardo Gonçalves
Fernando J. Von Zuben