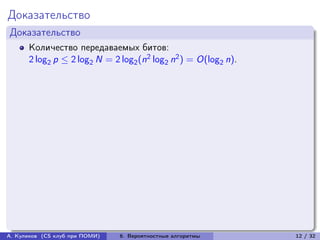
Лекция рассматривает вероятностные алгоритмы, в частности, алгоритмы для проверки перемножения матриц и сравнения строк. Описаны методы, позволяющие достичь значительного ускорения проверки через использование вероятностных подходов, снижая сложность работы до O(n²). Приведены алгоритмы, такие как rand-matrix-equiv и rand-string-equiv, которые демонстрируют, как можно эффективно проводить данные проверки с минимальной вероятностью ошибки.





































![Алгоритм
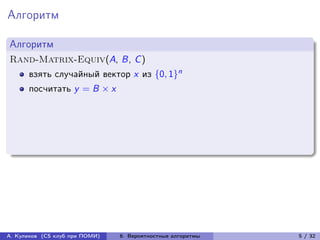
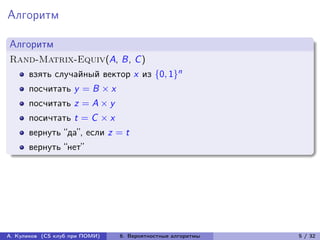
Алгоритм
Rand-String-Equiv(a, b)
Пусть |a| = |b| = n, N = n2 log2 n2 .
Выберем случайно простое число p из интервала [2..N].
А. Куликов (CS клуб при ПОМИ) 6. Вероятностные алгоритмы 11 / 32](https://image.slidesharecdn.com/20071111efficientalgorithmskulikovlecture06-100803081459-phpapp01/85/20071111-efficientalgorithms-kulikov_lecture06-42-320.jpg)
![Алгоритм
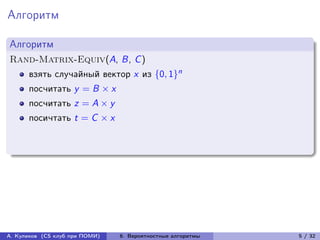
Алгоритм
Rand-String-Equiv(a, b)
Пусть |a| = |b| = n, N = n2 log2 n2 .
Выберем случайно простое число p из интервала [2..N].
Выдать “да”, если a mod p = b mod p.
А. Куликов (CS клуб при ПОМИ) 6. Вероятностные алгоритмы 11 / 32](https://image.slidesharecdn.com/20071111efficientalgorithmskulikovlecture06-100803081459-phpapp01/85/20071111-efficientalgorithms-kulikov_lecture06-43-320.jpg)
![Алгоритм
Алгоритм
Rand-String-Equiv(a, b)
Пусть |a| = |b| = n, N = n2 log2 n2 .
Выберем случайно простое число p из интервала [2..N].
Выдать “да”, если a mod p = b mod p.
Выдать “нет”.
А. Куликов (CS клуб при ПОМИ) 6. Вероятностные алгоритмы 11 / 32](https://image.slidesharecdn.com/20071111efficientalgorithmskulikovlecture06-100803081459-phpapp01/85/20071111-efficientalgorithms-kulikov_lecture06-44-320.jpg)
![Алгоритм
Алгоритм
Rand-String-Equiv(a, b)
Пусть |a| = |b| = n, N = n2 log2 n2 .
Выберем случайно простое число p из интервала [2..N].
Выдать “да”, если a mod p = b mod p.
Выдать “нет”.
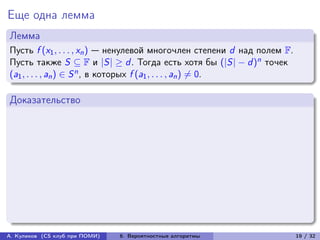
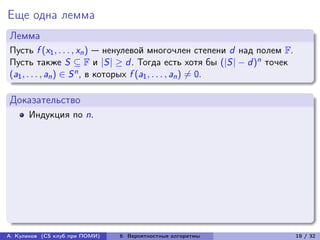
Лемма
Алгоритм Rand-String-Equiv является вероятностным алгоритмом
с односторонней ошибкой с вероятностью ошибки O(1/n) и требует
передачи O(log n) битов.
А. Куликов (CS клуб при ПОМИ) 6. Вероятностные алгоритмы 11 / 32](https://image.slidesharecdn.com/20071111efficientalgorithmskulikovlecture06-100803081459-phpapp01/85/20071111-efficientalgorithms-kulikov_lecture06-45-320.jpg)