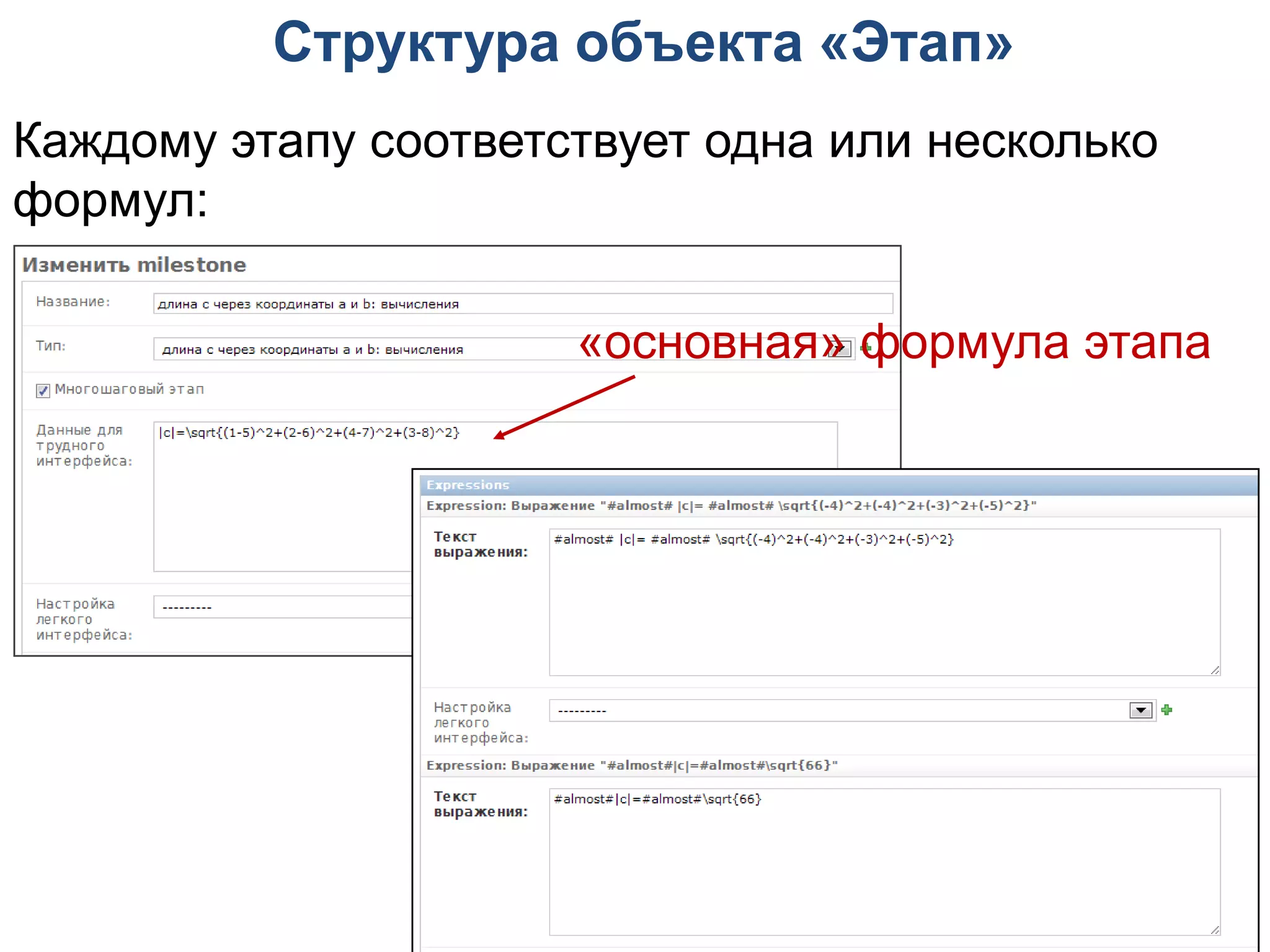
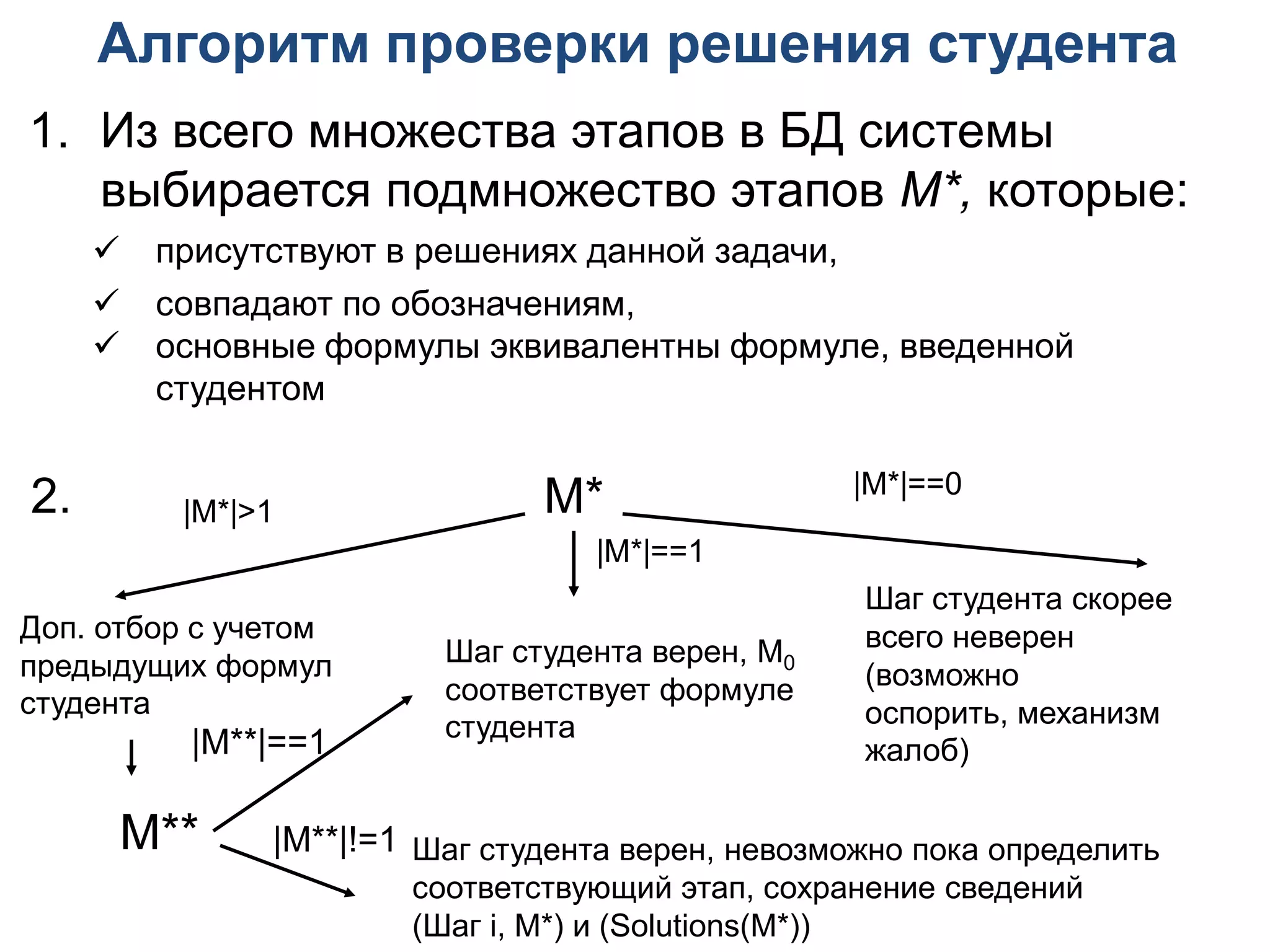
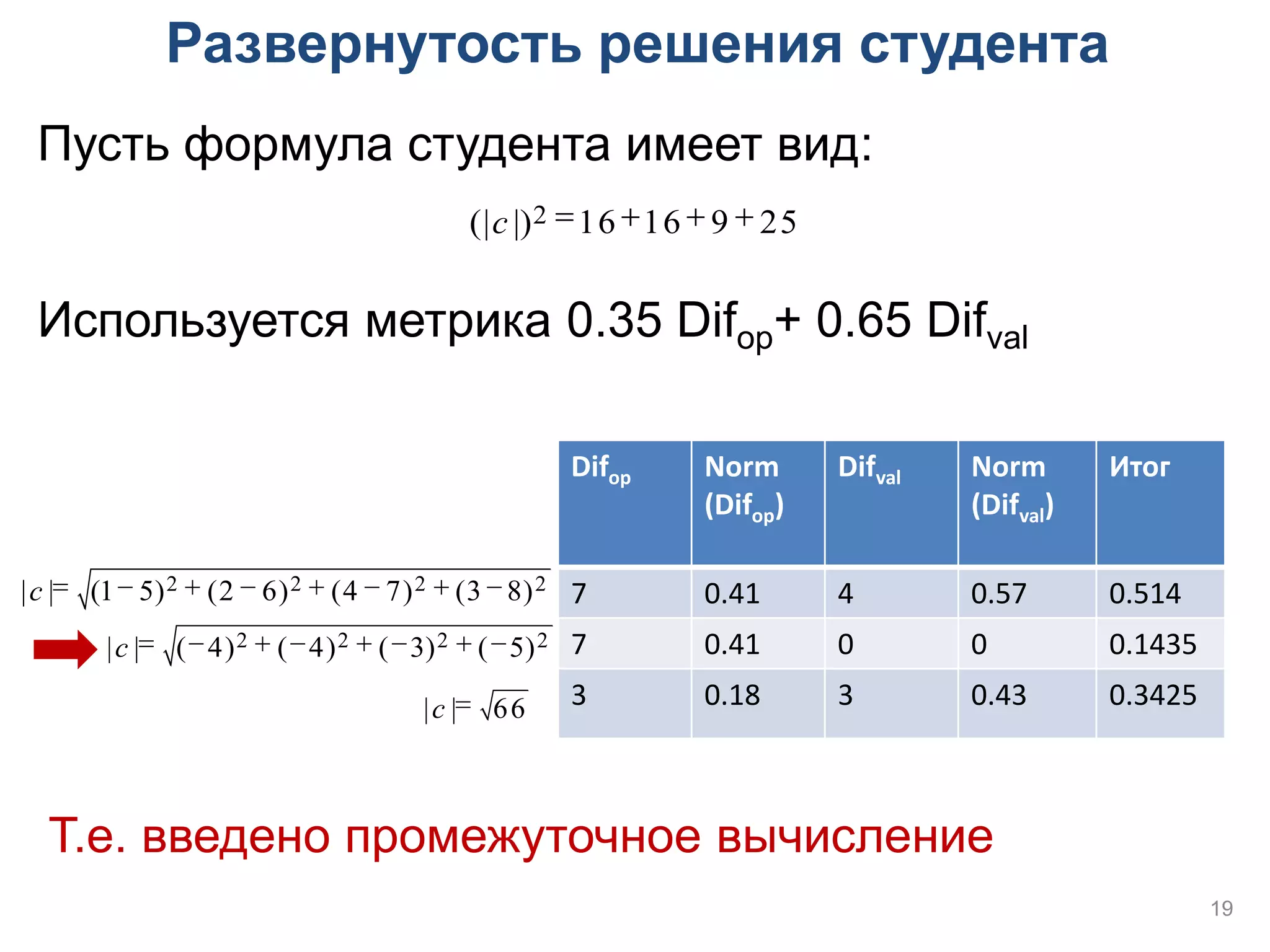
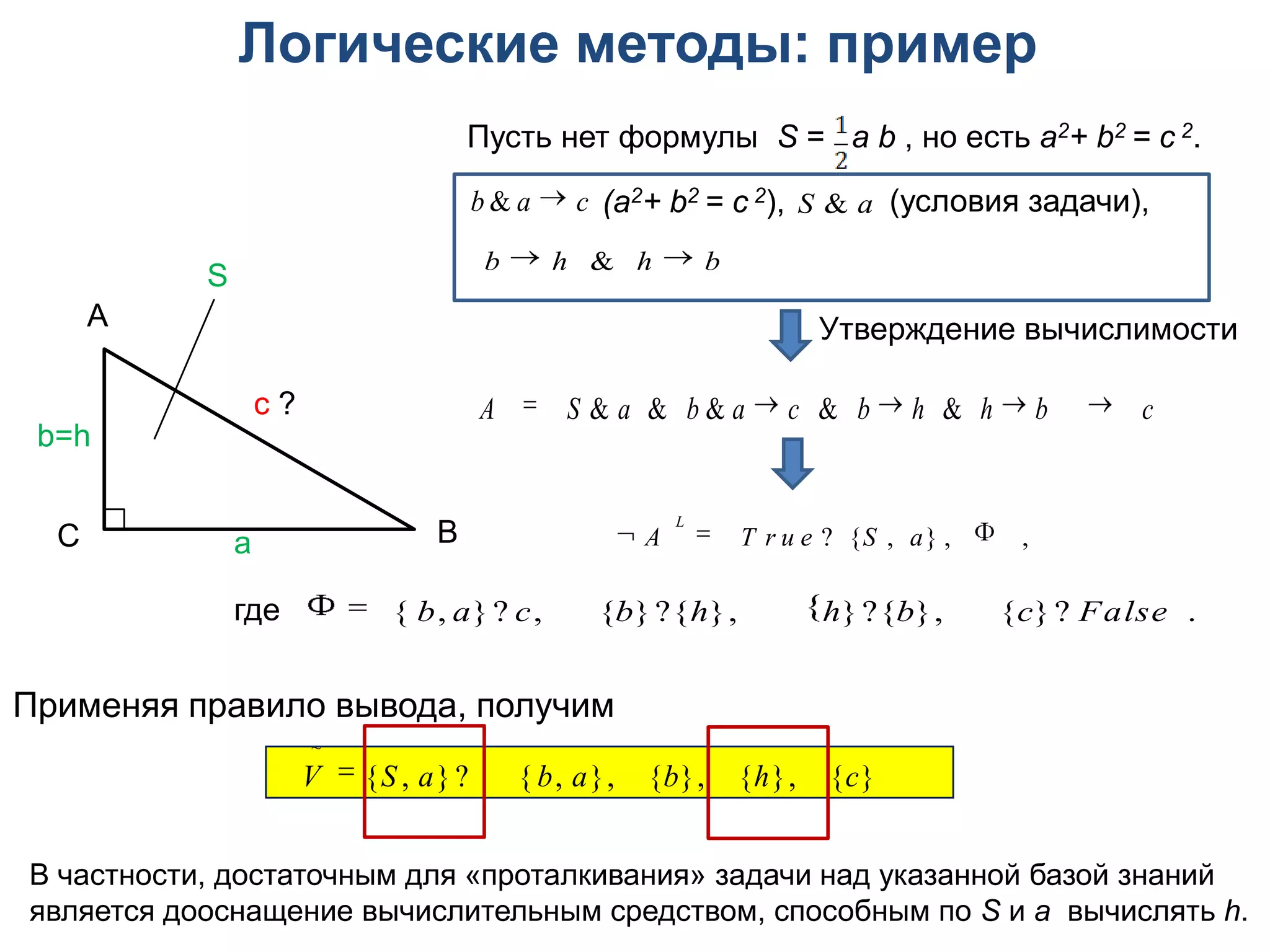
Документ описывает методы интеллектуализации обучающих систем, уделяя внимание эвристическим методам и многокритериальной оптимизации в контексте системы "Волга". Обсуждаются различные подходы к проверке решений учебных задач, включая алгоритмы оценки корректности действий студента и проблемы составления эквивалентных формул. Кроме того, рассматриваются ограничения существующих систем и возможности применения логических методов в образовательных технологиях.

1. Методы интеллектуализации
обучающих систем
Васильев С.Н., Смирнова Н.В., Суконнова А.А.,
Душкин Д.Н., Абраменков А.Н.
ИПУ РАН им. В.А. Трапезникова
2012

2. Интеллектуализация ИОС «Волга»
 Эвристические методы и
многокритериальная оптимизация:
 проверка решений учебных задач
 Логические методы:
 генерация решений учебных задач
 управление учебным процессом

3. Часть 1.
Проверка решений учебных
задач

4. Другие системы авт. обучения
Современные ведущие системы дистанционного
обучения имеют существенные ограничения на
форму ответов обучаемых.

5. Другие системы авт. обучения

6. Пользовательский интерфейс решения
задачи в ИОС «Волга»
6

7. Другие пользовательские интерфейсы
ввода шага
7

8. Техническая платформа ИОС «Волга»
• Веб-приложение с архитектурой «клиент-
сервер»
• Сервер:
– язык Python, платформа Django
– Python-библиотека символьных
вычислений SymPy
(альтернатива – Maxima)

9. Инструменты символьных
вычислений (ИСВ) и проверка ответов
При проверке ответов ИСВ можно использовать
для определения эквивалентности пар формул
Для того, чтобы проверить с помощью SymPy
эквивалентны ли x + y = 5 и 5 = y + x
нужно написать:
if (simplify (exp1part1 – exp1part2 – exp2part1 +
exp2part2) == 0 or simplify(exp1part1 – exp1part2 –
exp2part2 + exp2part1) == 0)
return true;

10. Проблема алгоритмической
неразрешимости задачи эквивалентности
термов
 Еще в 1970-х гг. (Глушков В.М. и др.)
отмечалась полезность практической
разрешимости, учитывающей эвристики и
вычислительную сложность задач
 в ИОС не закладываются задачи высокой
вычислительной сложности
 предусматривается механизм действий в
случае невозможности верификации шага
студента

11. Сведения о возможных решениях
учебных задач
Возможные решения учебных задач представляются
посредством коллекций ссылок на экземпляры
класса «Этап»
Задача
Решение 1 Решение k
…
Этап 1 Этап 1
… …
Этап n …
Этап m
11

12. Сведения о возможных решениях
учебных задач
Так выглядит панель настройки решения задачи:
12

13. Структура объекта «Этап»
Каждому этапу соответствует одна или несколько
формул:
«основная» формула этапа
13

14. Алгоритм проверки решения студента
Рассмотрим алгоритм проверки на следующем
примере:
14

15. Алгоритм проверки решения студента
1. Из всего множества этапов в БД системы
выбирается подмножество этапов M*, которые:
 присутствуют в решениях данной задачи,
 совпадают по обозначениям,
 основные формулы эквивалентны формуле, введенной
студентом
|M*|==0
2. |M*|>1 M*
|M*|==1
Шаг студента скорее
Доп. отбор с учетом всего неверен
предыдущих формул Шаг студента верен, M0
соответствует формуле (возможно оспорить,
студента механизм жалоб)
студента
|M**|==1
M** |M**|!=1 Шаг студента верен, невозможно пока определить
соответствующий этап, сохранение сведений
(Шаг i, M*) и (Solutions(M*))

16. Пример: оценка полноты решения
Пусть формула студента:(|c |)2 16 16  9  25
16

17. Пример: оценка полноты решения
Пусть формулы студента:
(|c |)2  (a1  b1)2  (a2  b2 )2  (a3  b3)2  (a4  b4 )2, затем (|c |)2 16 16  9  25
17

18. Развернутость решения студента
Как определить, какой случай имеет место:
 конечное значение,
 промежуточное вычисление,
 формула, в которую подставлены цифры?
Полезна метрика на основе суммы модулей разниц
в количестве операций ‘+’, ‘-’, ‘*’, ‘**’ (Difop) и в
количестве цифр и обозначений (‘Difval’):
0.35 Difop+ 0.65 Difval
18

19. Развернутость решения студента
Пусть формула студента имеет вид:
(|c |)2 16 16  9  25
Используется метрика 0.35 Difop+ 0.65 Difval
Difop Norm Difval Norm Итог
(Difop) (Difval)
| c | (1 5)2  (2  6)2  (4  7)2  (3  8)2 7 0.41 4 0.57 0.514
| c | (4)2  (4)2  (3)2  (5)2 7 0.41 0 0 0.1435
| c | 66 3 0.18 3 0.43 0.3425
Т.е. введено промежуточное вычисление
19

20. Проблема множественности
комбинаций формул, генерируемых
студентами при решении задач
Набор «базовых» формул для задачи вычисления
расстояния между векторами:
p(a,b) |c | (1)
|c | (c,c) (2)
(c,c)  c12  c2
2 (3)
ci  ai  bi ,i 1,...,4 (4)
Комбинация (1) и (2): p(a,b)  (c,c)
Комбинация (2) и (3): |c | c12  c22
В рассматриваемом примере нужно заложить >16
решений!

21. Проблема множественности
комбинаций формул: решение
Пусть формула студента - |c | c1  c2
(1)
p(a,b) |c | (1)
|c | (c,c) (2)
(2)
(c,c)  c12  c2
2 (3)
ci  ai  bi ,i 1,...,4 (4) (3)
Формируем комбинацию (2) (4)
и (3): |c | c12  c22
Сравниваем: c12  c22  c1  c2 «Комбинаторный» этап
Шаг студента неверен.

22. Ограничения предложенного способа
проверки решений: simplify
Как можно описать класс выражений, для которых функция
simplify всегда выдает результат?
Разработчики SymPy: обычно выражение не упрощается по одной из
следующих причин:
1) требуемое упрощение очень сложное,
2) упрощение неприменимо для некоторых значений переменных*
*В процессе работы simplify не используются упрощения, которые
не являются применимыми для всех комплексных чисел.
Например, x  x верно только тогда, когда x – положительное
число. Этих ограничений можно избежать путем дополнительных
настроек.

23. Часть 2.
Логические методы

24. Логические методы
 Метод позитивно-образованных формул (ПОФ)
 Формулы представляются как деревья
 J – пропозициональный фрагмент исчисления
ПО-формул
 В соответствии с методом доказательства от
противного, выводы в исчислении J
ориентированы на опровержение отрицания
доказываемого (после применений правила 
формула должна свестись к True?-False)

25. Логические методы
Утверждение. Пусть задача A имеет вид F  G , L
L  
Где  F  - хорновская по-формула,  G  - из класса

B ?  B1,..., Bn  . Тогда всякий ограниченный (, ) -
процесс синтеза условия V выводимости формулы
~
 F &G  конечен и конструктивен, а
L
~
синтезируемое решение V - спецификация
искомого, логически минимального,
конструктивного дооснащения

26. Логические методы: пример
Пусть нет формулы S = a b , но есть a2+ b2 = с 2.
b & a  c (a2+ b2 = с 2), S & a (условия задачи),
S b  h  & h  b
А Утверждение вычислимости
c? A  S & a & b & a  c  & b  h  & h  b  c
b=h
В   A   T r u e ? {S , a} ,   ,
L
С a
где   { b, a}? c, {b}?{h}, h}?{b}, {c}? False  .
Применяя правило вывода, получим
~
V  {S , a}? { b, a}, {b}, {h}, {c} 
В частности, достаточным для «проталкивания» задачи над указанной базой знаний
является дооснащение вычислительным средством, способным по S и a вычислять h.

27. Спасибо за внимание!