Документ представляет собой теоретическую информацию о нечётких множествах, подробно описывающую их свойства, операции и применение в алгоритмах и моделях. Он включает определения, операции над нечёткими множествами, способы их введения и различные методики их оценки. Также рассматриваются т-нормы, декомпозиция и расстояния между нечёткими множествами.

![Теория нечётких множеств 2 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Обычное множество
ХХааррааккттееррииссттииччеессккааяя ффууннккцциияя ооббыыччннооггоо ччёёттккооггоо ммнноожжеессттвваа
.,0
,,1
)(
Ax
Ax
xhA
ГГддее ооппррееддееллееннаа??
((ууннииввееррссааллььннооее ммнноожжеессттввоо))
АА еессллии ббууддеетт ппррииннииммааттьь ззннааччеенниияя иизз ]1,0[ ??](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-2-2048.jpg)




![Теория нечётких множеств 7 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Определение
Пусть задано множество U (базовое множество)
и функция ]1,0[: UA (степень принадлежности),
тогда нечётким (размытым) подмножеством A называется график
}|))(,{( Uuuu A
Множество (L-R)-типа
Нечётких подмножеств множества больше, чем чётких!](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-7-2048.jpg)


![Теория нечётких множеств 10 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Операции
равенство
BABA
включение
BABA
дополнение
BABA 1
пересечение ],min[ BABA
объединение ],max[ BABA
алгебраическое произведение
BABA
алгебраическая сумма
BABABA
пустое и универсальное
множества
0 , 1U](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-10-2048.jpg)





![Теория нечётких множеств 16 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Пересечение можно вводить по разному!
Т-нормы
],min[ BABA (1)
BABA (2)
]1,0max[ BABA (3)
]))1()1((,1min[1 /1 pp
B
p
ABA
(4)
]]1[],1[max[ BAABBA II (5)](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-16-2048.jpg)
![Теория нечётких множеств 17 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Аксиоматическое определение Т-нормы
(треугольной нормы)
]1,0[]1,0[]1,0[:
0)0,0(
AAA ),1()1,(
),(),( ABBA
)),,(()),(,( CBACBA
),(),(),(),( DCBADCBA
В чётком случае– обычное пересечение
Как ввести объединения?](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-17-2048.jpg)
![Теория нечётких множеств 18 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Как ввести объединения
Можно по правилам де Моргана
],max[]1,1min[1],min[ BABABA
BABABABA )1()1(1](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-18-2048.jpg)
![Теория нечётких множеств 19 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Объединение тоже можно вводить по разному!
Т-конормы
],max[ BABA (1)
BABABA (2)
],1min[ BABA (3)
]))()((,1min[ /1 pp
B
p
ABA
(4)
.0,0,1
,0,
,0,
BA
AB
BA
BA
(5)
Аналогично – есть аксиоматический подход...
Поэтому это не теория вероятностей – больше алгебры и эвристик](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-19-2048.jpg)
![Теория нечётких множеств 20 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Задача 2
Кстати,
1],))()((,1min[ /1
ppp
B
p
ABA
Чему равен
]))()[((lim /1 pp
B
p
A
p
?
Докажите.](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-20-2048.jpg)

![Теория нечётких множеств 22 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Задача (решение сразу)
Как определить выпуклое нечёткое множество?
)](),(min[))1((]1,0[, yxyxRyx AAA
тогда и только тогда, когда все уровни выпуклые!
Как определить декартово произведение нечётких множеств?
)](),(min[),( yxyx BABA ](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-22-2048.jpg)




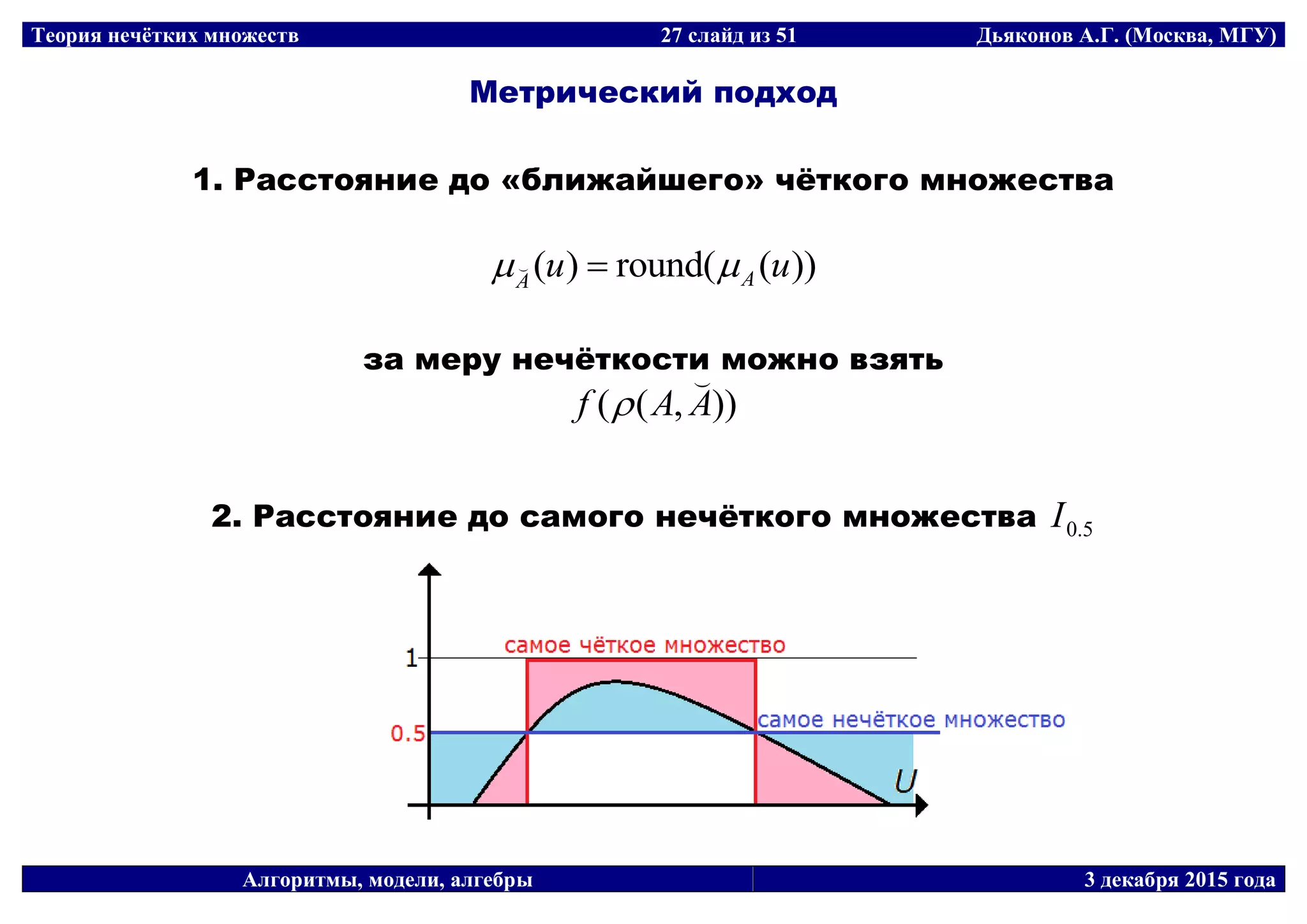


![Теория нечётких множеств 31 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Декомпозиция отношений
000
0105.0,
100
0104.0,
110
0111.0max
4.01.00
05.01.0
max-min-композиция отношений
YXR ~
ZYL ~
ZXLR ~
)]],(),,([min[max),( zyyxzx LR
y
LR
для композиции надо выполнить своеобразное умножение матриц
2.02.0
3.02.0
3.00
02.0
5.01
2.011.0
5.02.00
в композиции
можно использовать max-произведение
и max-среднее арифметическое](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-31-2048.jpg)

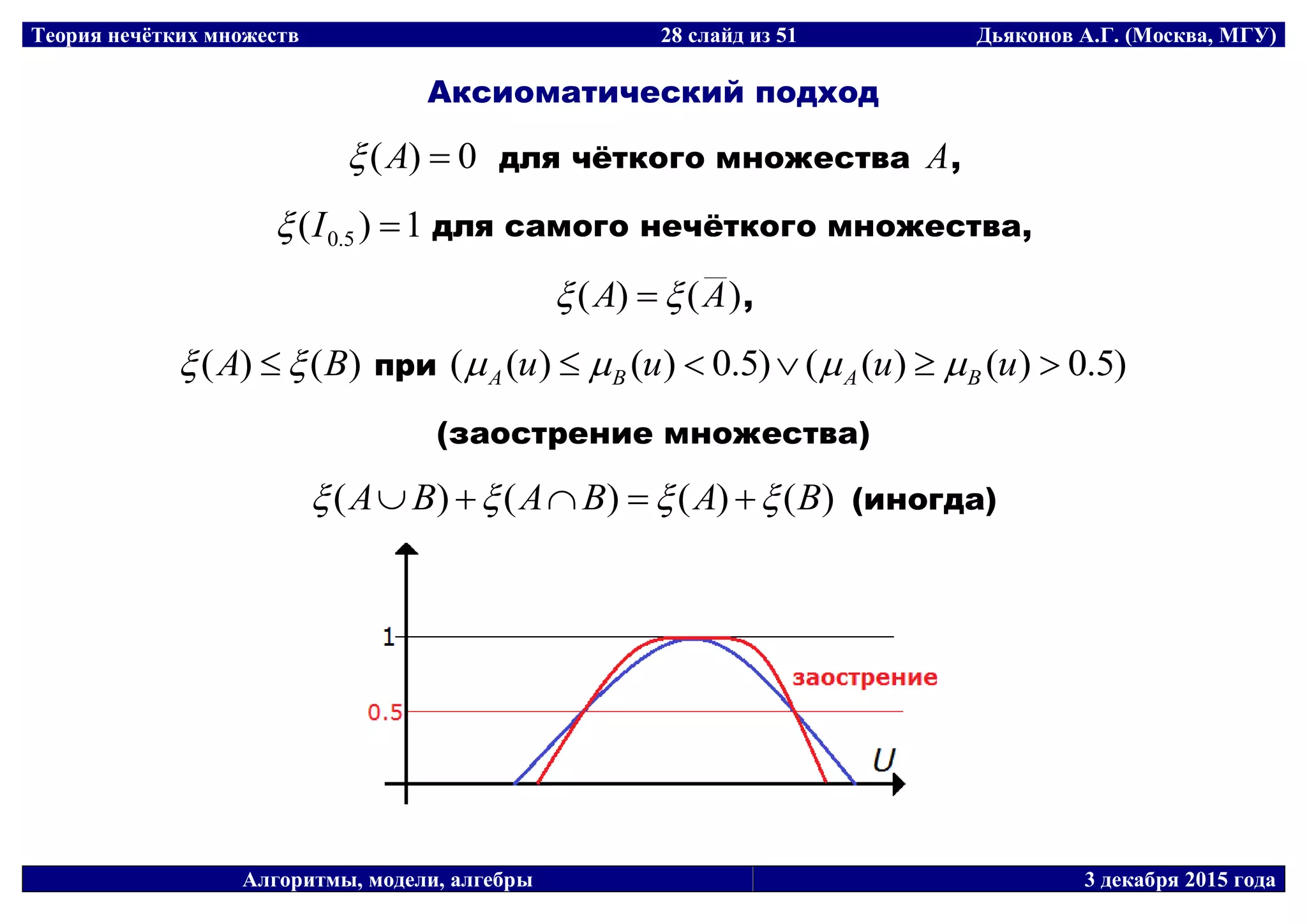
![Теория нечётких множеств 33 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Отношение R в UU
рефлексивное, если 1),( uuUu R
симметричное, если ),(),(),( 122121 uuuuUUuu RR
транзитивное, если )],(),,([max),(),,( 3
zyyxzxUzyx RR
y
R
можно «красивее»: RRR
Подобие = рефлексивное + симметричное + транзитивное
~ декомпозируется на чёткие эквивалентности
Как это использовать в машинном обучении?
Примеры...](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-33-2048.jpg)

![Теория нечётких множеств 36 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Образ нечёткого множества при отображении
YXf :
)(sup)(
)(1
xy A
yfx
B
Принцип обобщения (внимание!)
– основан на этой формуле
Пусть, например, нечёткие множества – нечёткие числа, тогда
)](),(min[sup)( yxy BA
yxz
BA
аналогично другие операции над нечёткими числами
~ уравнения с нечёткими числами](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-36-2048.jpg)
()( uuu RRR
(здесь всё эвристично)
Пример эвристического вывода
«Если товар дорогой, то надёжный»
«Товар очень дорогой» «Товар очень надёжный»](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-37-2048.jpg)
![Теория нечётких множеств 38 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Немного о нечётком выводе и т.п.
Обобщение импликации
)]()(1,1min[),( vuvu BABA ](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-38-2048.jpg)



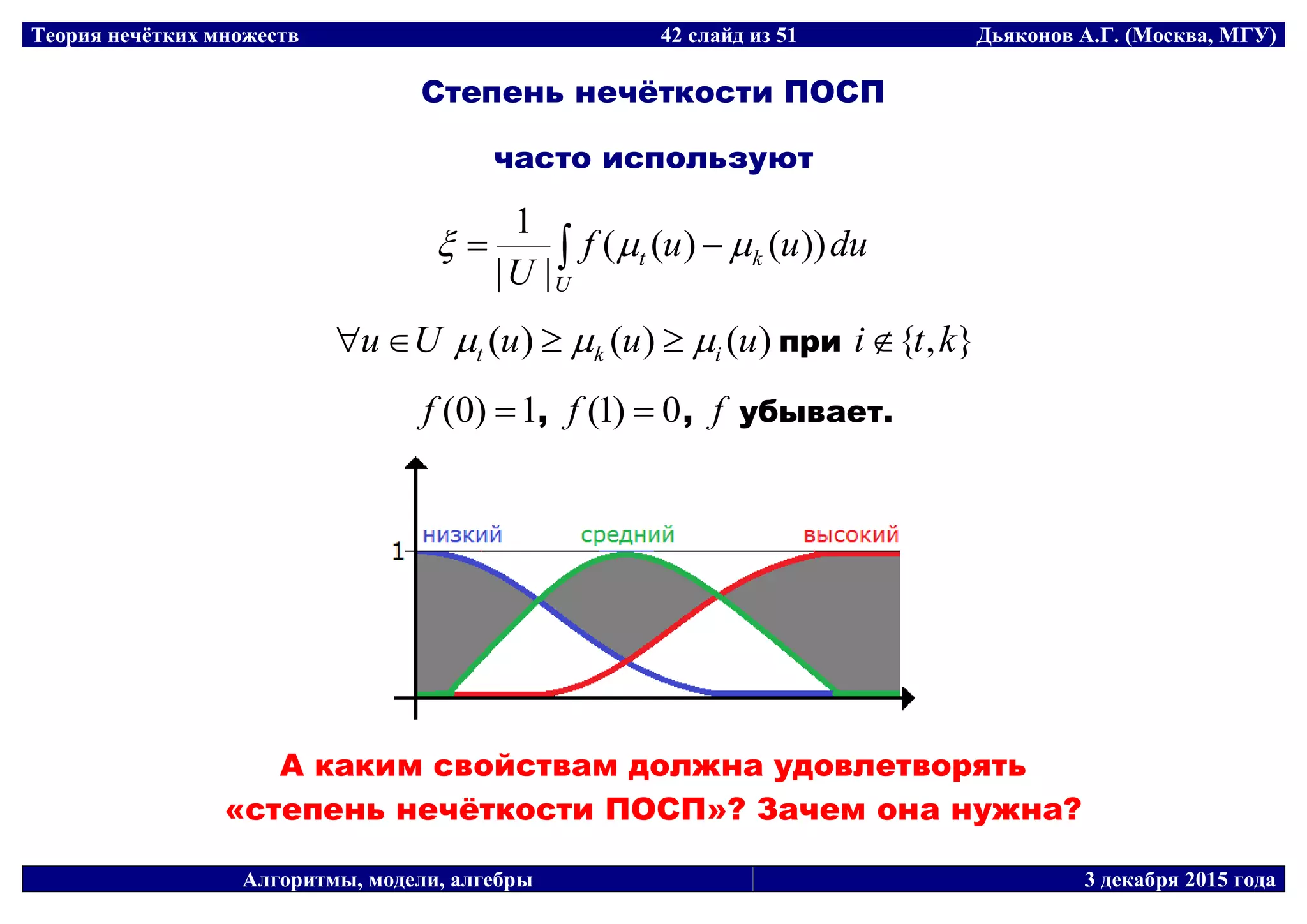

![Теория нечётких множеств 44 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Нечёткие задачи...
Какое из множеств более нечёткое:
)}9.0,3(),6.0,2(),3.0,1{( , )}75.0,2(),25.0,1{( ?
Дано нечёткое число «один»:
],2,0[,0
],2,1[,2
],1,0[,
)(
u
uu
uu
uодин
чему равно число «два»= «один»+ «один»?
Чему равно число «два»= 2*«один»?
В каком случае «ноль»+ «один» = «один»?](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-44-2048.jpg)
![Теория нечётких множеств 45 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Решение задачи 1
Какие из равенств всегда выполняются?
,,);(U ,,);(U
)()()( CABACBA Неверно!
BABA )(
A
AA
AUA
UUA
UAA )( Неверно! Неверно!
)( AA Неверно! Неверно!
Как решать: непосредственная проверка
)],min(),,max[min()],max(,min[ cabacba ](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-45-2048.jpg)

![Теория нечётких множеств 47 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Решение задачи 2
Чему равен
]))()[((lim /1 pp
B
p
A
p
?
],max[]))()[((lim /1
BA
pp
B
p
A
p
Пусть BA , A
pp
A
B
p
A
pp
B
p
A
p
/1
/1
1lim]))()[((lim .
0
)1ln(
1lnlim
/1
p
x
x
p
pp
p
, 10 x](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-47-2048.jpg)


![Теория нечётких множеств 50 слайд из 51 Дьяконов А.Г. (Москва, МГУ)
Алгоритмы, модели, алгебры 3 декабря 2015 года
Решение задачи 5
Транзитивное замыкание 32
RRRL транзитивно.
LRRRRRRL 32222
)()(
Решение задачи 6
Для предпорядка 32
RRR
)]],(),,([min[max),(2 zyyxzx RR
yR
),()],(,),(min[)]],(),,([min[),(
1
2 zxzxxxzyyxzx RRRxyRRR
С другой стороны, по транзитивности ),(),(2
2
zxzxRR RR
поэтому ),(),(2 zxzx RR
и RR 2
«Домножая на R» получаем и другие равенства.](https://image.slidesharecdn.com/ama201512fuzzy-151203203055-lva1-app6892/75/slide-50-2048.jpg)
