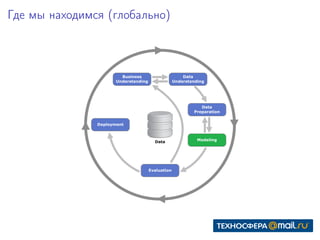
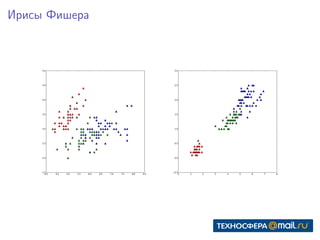
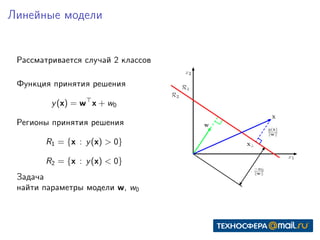
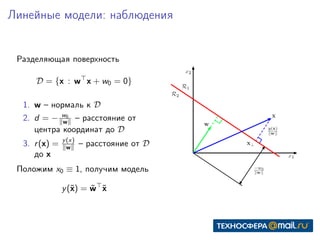
Документ представляет собой конспект занятия по линейным моделям в области data science. Он охватывает темы выбора модели, оптимизации параметров, классификации, а также различные подходы, такие как метод максимального правдоподобия и байесовский вывод. В конце приведены практические задания и ключевые даты для выполнения.

1. Введение в Data Science
Занятие 2. Линейные модели
Николай Анохин Михаил Фирулик
10 марта 2014 г.

2. Где мы находимся (глобально)

3. Где мы находимся (локально)
M Выдвигаем гипотезу насчет модели - семейства
параметрических функций вида
Y = {y(x, θ) : X × Θ → T},
которая могла бы решить нашу задачу (model selection)
L Выбираем наилучшие параметры модели θ∗
, используя
алгоритм обучения
A(X, T) : (X, T)N
→ Y
(learning/inference)
D Используя полученную модель y∗
(x) = y(x, θ∗
),
классифицируем неизвестные объекты (decision making)

4. Как выбрать параметры модели?
Решить задачу оптимизации, чтобы получить значения θ∗
Варианты подходов
θ – фиксировано, но неизвестно: ищем θ, согласующееся с
обучающей выборкой
θ – случайная величина, распределенная по известному закону:
ищем параметры распределения

5. Обобщенные линейные модели
Метод максимального правдоподобия
Байесовский вывод

6. 8 марта (is coming)
Setosa Versicolor Virginica
Задача
Определить вид ириса на основании длины чашелистика, ширины
чашелистика, длины лепестка и ширины лепестка.

7. Ирисы Фишера

8. Линейные модели
Рассматривается случай 2 классов
Функция принятия решения
y(x) = w x + w0
Регионы принятия решения
R1 = {x : y(x) > 0}
R2 = {x : y(x) < 0}
Задача
найти параметры модели w, w0

9. Линейные модели: наблюдения
Разделяющая поверхность
D = {x : w x + w0 = 0}
1. w – нормаль к D
2. d = − w0
w – расстояние от
центра координат до D
3. r(x) = y(x)
w – расстояние от D
до x
Положим x0 ≡ 1, получим модель
y(˜x) = ˜w ˜x

10. Обобщенные линейные модели
Линейная модель
y(x) = w0 + wi xi
Квадратичная модель
y(x) = w0 + wi xi + wij xi xj
Обобщенная линейная модель
g(x) = ai φi (x) = a y

11. Случай линейно разделимых классов
Обобщенная линейная модель
g(x) = ai φi (x) = a y
Дана обучающая выборка Y = {y1, . . . , yN }
Идея
Преобразовать объекты второго класса в обратные им и решать
задачу оптимизации в области aT
yi > 0, ∀i

12. Задача оптимизации
Задача
Минимизируем критерий J(a) при условиях aT
yi > 0, ∀i
Пусть Y – множество неправильно проклассифицированных
объектов
Je(a) = y∈Y 1
Jp(a) = y∈Y −a y
Jq(a) = y∈Y (a y)2
Jr (a) = y∈Y
(a y)2
−b
y
Улучшение: добавить отступы

13. Градиентный спуск
1. initialise a, J(a), η(k), , k = 0
2. do k ← k + 1
3. a ← a − η(k) J(a)
4. until η(k) J(a) <
5. return a
5. end

14. Инкрементальный алгоритм
Рассматриваем Jr (a) = y∈Y
(a y)2
−b
y
1. initialise a, η(k), k = 0
2. do k ← k + 1
3. if yk is misclassified a ← a − η(k)(a yk)2
−b
yk
2 yk
4. until no errors left
5. return a
6. end

15. Случай линейно неразделимых классов
Использовать η(k) → 0 при k → ∞
От системы неравенств перейти к системе линейных уравнений
Линейное программирование

16. Снова переобучение
Оптимизируем критерий с регуляризацией
J1(a) = J(a) + λJR (a)
λ – коэффициент регуляризации
JR (a) = |aj |q

17. Перцептрон: результаты

18. Метод максимального правдоподобия
Задача
Дана обучающая выборка X. Предполагая, что распределение p(x|θ)
известно, найти значения параметров θ.
Интуиция: найти такие θ, которые максимизируют вероятность
P(X|θ).
При предположении, что обучающие образцы независимы, имеем
P(X|θ) = p(xi |θ)
Функция правдоподобия
l(θ) = log P(X|θ) = log p(xi |θ)
Требуется найти
θ = arg max
θ
l(θ)

19. Нормальное распределение
p(x|µ) =
1
σ
√
2π
e−
(x−µ)2
2σ2
Задача
Дана выборка X объектов x, распределенных согласно одномерному
нормальному закону N(µ, σ2
). Используя принцип максимального
правдоподобия, оценить значение µ при известном значении σ.

20. Вероятностная линейная модель
Рассматриваем 2 класса
p(C1|x) =
p(x|C1)p(C1)
p(x|C1)p(C1) + p(x|C2)p(C2)
=
1
1 + e−a
= σ(a)
a = ln
p(x|C1)p(C1)
p(x|C2)p(C2)
σ(a) – сигмоид-функция, a = ln(σ/(1 − σ))
Упражнение: p(x|Ck ) = N(µk , Σ). Проверить, что
p(Ck |x) = σ(w x + w0)

21. (Еще более) обобщенная линеная модель
Базисные функции φn(x)
φn(x) = exp −
(x − µn)2
2s2
Функция активации f (a)
f (a) = σ(a)
(Совсем) обобщенная линейная
модель
y(x, w) = f (w φ(x))

22. Логистическая регрессия
дано
{φn = φ(xn), tn}, tn ∈ {0, 1}, n = 1 . . . N
модель
p(C1|φ) = y(φ) = σ(w φ)
функция правдоподобия
l(w) = log
N
n=1
ptn
(C1|φn)(1 − p(C1|φn))1−tn
=
=
N
n=1
tn log p(C1|φn) + (1 − tn) log(1 − p(C1|φn)) = −Je(w)
градиент
Je(w) =
N
n=1
(p(C1|φn) − tn)φn → minw

23. Логистическая регрессия: результаты

24. Байесовский вывод
Дано
плотность вероятности p(x|θ)
априорная плотность p(θ)
выборка X = {x1, . . . , xN }
Найти
апостериорную плотность p(θ|X)
p(x|X) = p(x|θ)p(θ|X)dθ
p(θ|X) =
p(X|θ)p(θ)
p(X|θ)p(θ)dθ
p(X|θ) =
n
p(xn|θ)

25. Мультиклассовая классификация
Задача
Использовать бинарный линейный классификатор для
мультиклассовой классификации Ирисов. Какие идеи?
Интерфейс классификатора clf
Использовать выборку x, y для обучения
clf.fit(x, y)
Предсказать класс объектов в x
y = clf.predict(x)
Предсказать вероятности классов для x
y = clf.predict_proba(x)
Вычислить значение функции решения в x
d = clf.decision_function(x)

26. Домашнее задание 1
Линейные модели
Реализовать на выбор
Линейная классификация методом градиентного спуска
Линейная регрессия методом градиентного спуска
Линейная классификация инкрементальным методом
Линейная регрессия инкрементальным методом
Ключевые даты
До 2014/03/14 23.59 выбрать задачу и ответственного в группе
До 2014/03/21 00.00 предоставить решение задания

27. Спасибо!
Обратная связь