Лекция охватывает задачи кластеризации, включая смесь нормальных распределений и методы EM и k-means. Обсуждаются принципы и этапы кластеризации, такие как определение похожести объектов, оценка качества моделей и необходимость разметки данных. Также рассматриваются различные алгоритмы и модификации кластера, критерии качества и проблемы, возникающие из-за высокой размерности данных.

1. Лекция 2
Задачи кластеризации
Николай Анохин
2 октября 2014 г.

2. План занятия
Задача кластеризации
Смесь нормальных распределений и EM
K-means и его модификации
1 / 30

3. Задача кластеризации
В задачах кластеризации целевая переменная не задана. Цель –
отыскать “скрытую структуру” данных.
Зачем вообще рассматривать задачи без целевой переменной?
1. разметка данных – дорогое удовольствие
2. можно сначала поделить, а потом разметить
3. возможность отслеживать эволюционные изменения
4. построение признаков
5. exploratory data analysis
2 / 30

4. Программисты python в Twitter
Графо-теоретические методы (источник)
3 / 30

5. Похожие тематики
Иерархическая кластеризия
4 / 30

6. Топ 1000 самых посещаемых доменов рунета
T-SNE + DBSCAN
5 / 30

7. Постановка задачи
Дано. N обучающих D-мерных объектов xi ∈ X, образующих
тренировочный набор данных (training data set) X.
Найти. Модель h∗
(x) из семейства параметрических функций
H = {h(x, θ) : X × Θ → N}, ставящую в соответствие произвольному
x ∈ X один из K кластеров так, чтобы объекты внутри одного
кластера были похожи, а объекты из разных кластеров различались.
Как определить похожесть объектов?
Как оценить качество модели?
Как выбрать K?
6 / 30

8. Многомерное нормальное распределение
N(x|µ, Σ) =
1
(2π)D/2
1
|Σ|1/2
exp −
1
2
(x − µ)T
Σ−1
(x − µ)
Параметры
D-мерный вектор средних D × D-мерная матрица ковариации
µ = xp(x)dx Σ = E[(x − µ)(x − µ)T
]
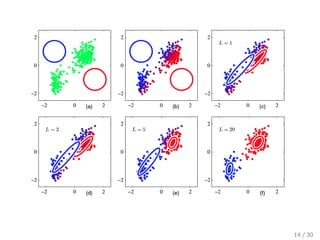
(a) D = 2 (b) (c) Σ = diag(σi ) (d) Σ = σI
7 / 30

9. Old Faithful data set
D = date of recordings in month (in August)
X = duration of the current eruption in minutes
Y = waiting time until the next eruption in minutes
(a) Yellowstone Park (b)
8 / 30

10. Смесь нормальных распределений
“Скрытая” K-мерная переменная z – принадлежность объекта к
одному из кластеров
p(zk = 1) = πk , zk ∈ {0, 1},
k
zk = 1 → p(z) =
k
πzk
k
Распределение x для каждого из K кластеров
p(x|zk) = N(x|µk , Σk ) → p(x|z) =
k
N(x|µk , Σk )zk
Смесь нормальных распределений
p(x) =
k
πk N(x|µk , Σk )
9 / 30

11. Апостериорная вероятность принадлежности к k кластеру
(априорная равна πk )
γ(zk ) = p(zk = 1|x) =
p(zk = 1)p(x|zk = 1)
K
j=1 p(zj = 1)p(x|zj = 1)
=
=
πk N(x|µk , Σk )
K
j=1 πj N(x|µj , Σj )
10 / 30

12. Maximum Likelihood (!)
ML принцип
Пусть дано семейство параметрических моделей h(x, θ). Выбираем
вектор параметров θ, максимизирующий функцию правдоподобия
(likelihood) p(D|θ), соответствующую рассматриваемому семейству
моделей.
Функция правдоподобия
log(X|π, µ, Σ) =
N
n=1
log
k
πk N(xn|µk , Σk ) → max
π,µ,Σ
Сложности
схлопывание компонент
переименование кластеров
невозможно оптимизировать аналитически
11 / 30

13. Дифференцируем функцию правдоподобия
Nk =
N
n=1
γ(znk ), µk =
1
Nk
N
n=1
γ(znk )xn
Σk =
1
Nk
N
n=1
γ(znk )(xn − µk )T
(xn − µk )
πk =
Nk
N
12 / 30

14. Expectation Maximization (!)
E Expectation: при фиксированных µk , Σk , πk
γ(znk ) =
πk N(xn|µk , Σk )
K
j=1 πj N(xn|µj , Σj )
M Maximization: при фиксированных γ(znk )
Nk =
N
n=1
γ(znk ), µk =
1
Nk
N
n=1
γ(znk )xn
Σk =
1
Nk
N
n=1
γ(znk )(xn − µk )(xn − µk )T
πk =
Nk
N
S Остановиться при достижении сходимости
13 / 30

15. 14 / 30

16. EM-алгоритм
Дано. Известно распределение P(X, Z|θ), где x – наблюдаемые
переменные, а z – скрытые.
Найти. θ, максимизирующее P(X|θ).
E вычислить P(Z|X, θold
) при фиксированном θold
M вычислить θnew
= arg maxθ Q(θ, θold
), где
Q(θ, θold
) = EZ[ln p(X, Z|θ)] =
Z
p(Z|X, θold
) ln p(X, Z|θ))
Улучшение: ввести априорное распределение p(θ)
15 / 30

17. K-means
Пусть Σk = I, тогда
p(x|µk , Σk ) =
1
√
2π
exp(−
1
2
x − µk
2
)
Рассмотрим стремление → 0
γ(znk ) =
πk exp(− 1
2 xn − µk
2
)
j πj exp(− 1
2 xn − µj
2)
→ rnk =
1, для k = arg minj xn − µj
2
0, иначе
Функция правдоподобия
EZ[ln p(X, Z|µ, Σ, π)] → −
N
n=1
K
k=1
rnk xn − µk
2
+ const
Вектор средних
µk = n rnk xn
n rnk
16 / 30

18. K-means
1 function kmeans(X, K):
2 initialize N # number of objects
3 initialize Mu = (mu_1 ... mu_K) # random centroids
4 do:
5 # E step
6 for k in 1..K:
7 for x in 1..N:
8 compute r_nk # Cluster assignment
9 # M step
10 for k in 1..K:
11 recompute mu_k # Update centroids
12 until Mu converged
13 J = loss(X, Mu)
14 return Mu, J
Сложность O(NK)
Локальная оптимизация (!)
17 / 30

19. 18 / 30

20. Задача
1 2 3 4 5
01234
19 / 30

21. Модификации k-means
На каждом шаге работаем с b случайно выбранными объектами
из каждого кластера (mini-batch k-means)
Критерий качества (k-medoids)
˜J =
N
n=1
K
k=1
rnk d(xn, µk )
d – функция расстояния, µk – один из объектов в кластере
20 / 30

22. Альтернативные функции расстояния
Def
Функция d(x, y) : X × X → R является функцией расстояния,
определенной на пространстве X тогда и только тогда, когда
∀x ∈ X, ∀y ∈ X, ∀z ∈ X выполнено:
1. d(x, y) ≥ 0
2. d(x, y) = 0 ⇔ x = y
3. d(x, y) = d(y, x)
4. d(x, y) ≤ d(x, z) + d(y, z)
21 / 30

23. Расстояния 1
Минковского
dr (x, y) =


N
j=1
|xj − yj |r


1
r
Евклидово r = 2
dE (x, y) = d2(x, y)
Манхэттэн r = 1
dM (x, y) = d1(x, y)
r = ∞
d∞(x, y) = max
j
|xj − yj |
22 / 30

24. Проблема
Функции расстояния чувствительны к преобразоаниям данных
Решение
Преобразовать обучающую выборку так, чтобы признаки имели
нулевое среднее и единичную дисперсию – инвариантность к
растяжению и сдвигу (standartize)
Преобразовать обучающую выборку так, чтобы оси совпадали с
главными компонентами матрицы ковариации – инвариантность
относительно поворотов (PCA)
23 / 30

25. Расстояния 2
Жаккар
dJ (x, y) = 1 −
|x ∩ y|
|x ∪ y|
Косинус
dc (x, y) = arccos
xy
x y
Правки
de – наименьшее количество
удалений и вставок, приводящее x к
y.
Хэмминг
dH – количество различных
компонент в x и y.
24 / 30

26. Проклятие размерности
Задача
Даны два случайных вектора x и y в пространстве размерности D.
Как зависит математическое ожидание косинус-расстояния между x
и y от размерности D?
dc (x, y) = arccos
D
j=1 xj yj
D
j=1 x2
j
D
j=1 y2
j
Наблюдения:
числитель стремится к нулю
знаменатель положительный
Вывод: dc (x, y) → π
2 .
25 / 30

27. Альтернативные критерии качества
Критерий
J =
K
k=1 xi ∈Ck
xi − mk
2
=
=
1
2
K
k=1
nk

 1
n2
k xi ∈Ck xj ∈Ck
xi − xj
2

 =
=
1
2
K
k=1
nk

 1
n2
k xi ∈Ck xj ∈Ck
s(xi , xj )

 =
1
2
K
k=1
nk¯sk
Примеры ¯si
sk = min
xi ,xj
s(xi , xj ); ¯sk = max
xi ,xj
s(xi , xj )
26 / 30

28. Кластеризация
Идея
Выбрать критерий качества кластеризации J и расстояние между
объектами d(xi , xj ) и вычислить разбиение выборки на кластеры,
которое которое соответствует оптимальному значению выбранного
критерия.
27 / 30

29. Качество кластеризации
Пусть дана обучающая выборка, для которой правильная
кластеризация C известна. С помощью выбранного алгоритма
получена кластеризация K. Проверить, насколько K совпадает с C.
Rand Index
a – кол-во пар объектов, попавших в один кластер и в C, и в K
b – кол-во пар объектов, попавших в разные кластеры и в C, и в K
RI =
a + b
CN
2
Mutual Information
MI =
c∈C k∈K
p(c, k) log
p(c, k)
p(k)p(c)
28 / 30

30. Задача
Дано: Сгенерированная смесь из гауссовских распределений
Требуется: Исследовать стабильность и чувствительность к
линейным преобразованиям алгоритма k-means
Пошаговая инструкция
1. Скачать и запустить шаблон кода на python
http://bit.ly/1yyVTyw
$ python kmeans.py -h
$ python kmeans.py
2. Заполнить функцию rand_index
Меняется ли rand от запуска к запуску?
3. Дописать функцию cluster_data
Реализовать N-times random restart
4. Как меняется результат кластеризации, если применить к
данным различные линейные преобразования?
29 / 30

31. Вопросы