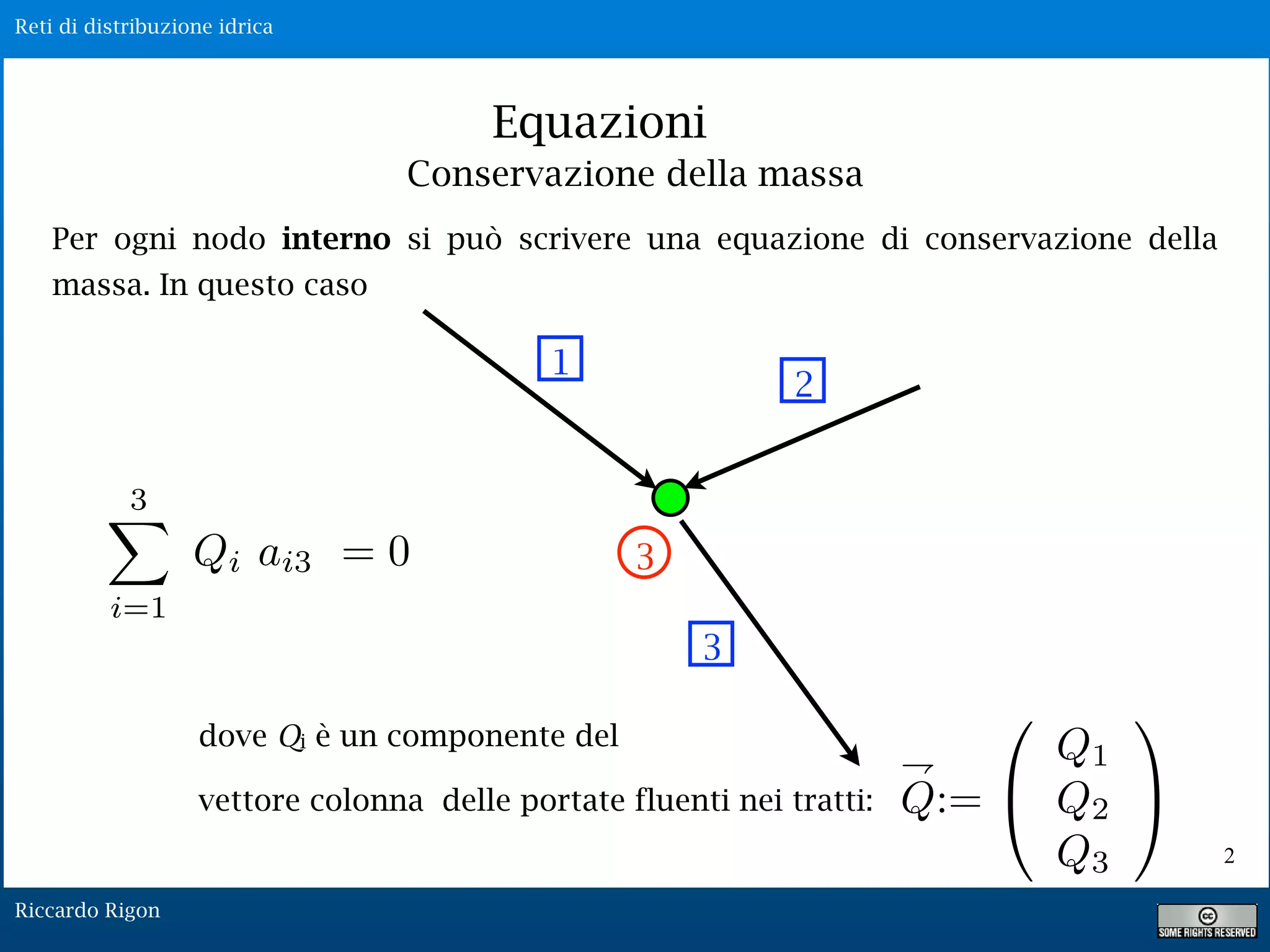
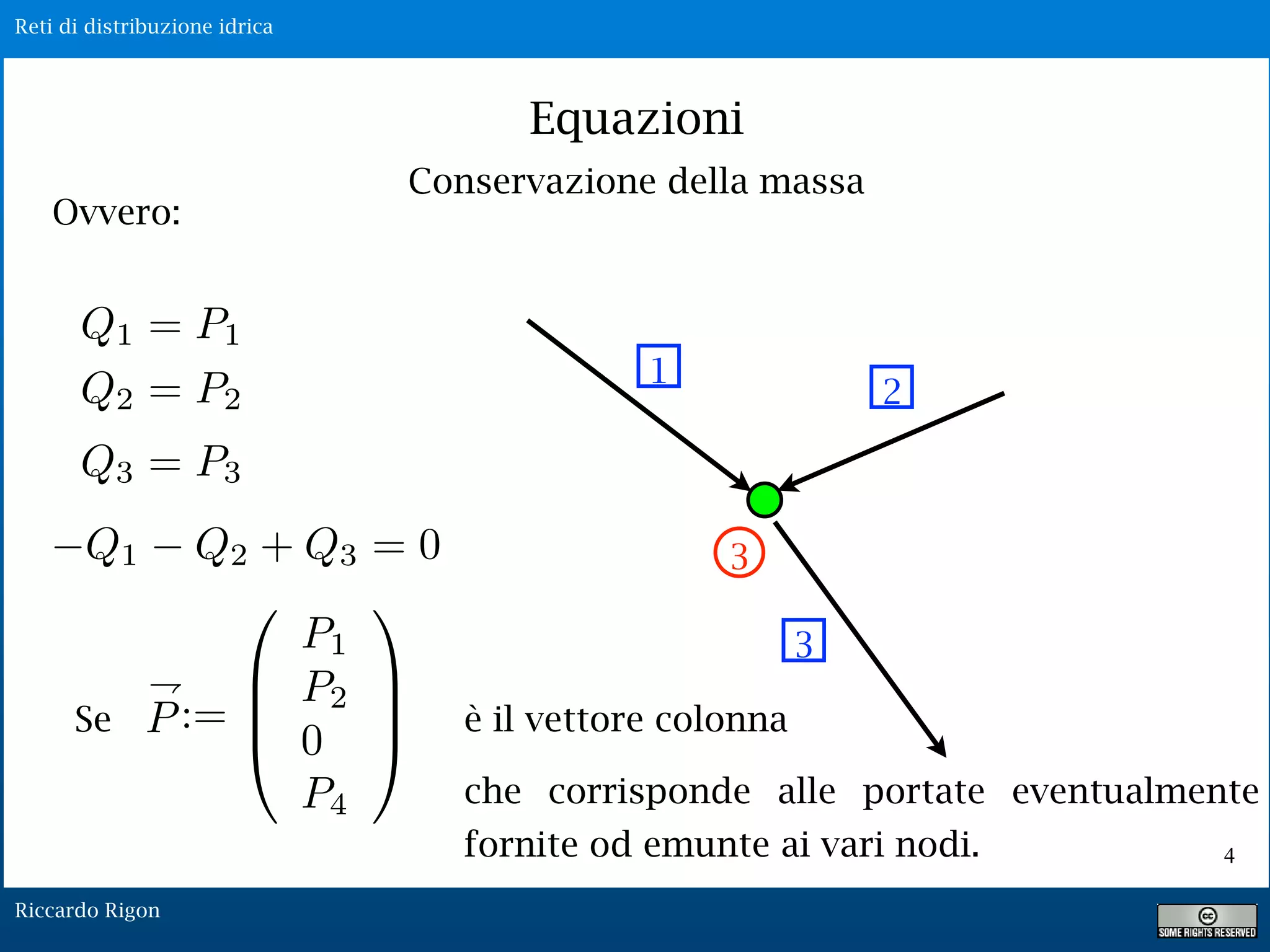
Il documento discute le equazioni di conservazione della massa nelle reti di distribuzione idrica, evidenziando la gestione delle portate nei nodi interni e le perdite di carico lungo le condotte. Viene inoltre analizzata la dissipazione dell'energia e si presentano formule come quelle di Darcy-Weisbach e Gaukler-Strickler per il calcolo delle perdite. Il sistema di equazioni risultante è non lineare, richiedendo un'adeguata assegnazione delle variabili per la risoluzione.