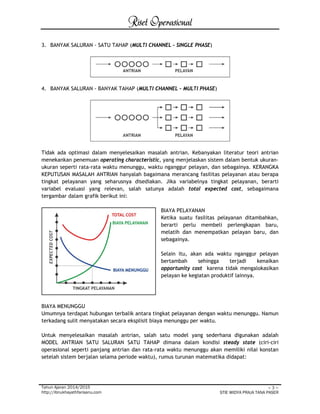
Dokumen tersebut membahas tentang teori antrian yang merupakan bidang ilmu yang melakukan penelitian untuk mengidentifikasi dan mengukur penyebab-penyebab serta konsekuensi-konsekuensi dari kegiatan mengantri. Teori antrian memiliki tiga komponen dasar yaitu kedatangan, pelayan, dan antrian. Dokumen tersebut juga menjelaskan empat model struktur antrian dasar dan contoh soal penerapan model antrian satu saluran