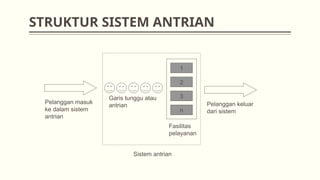
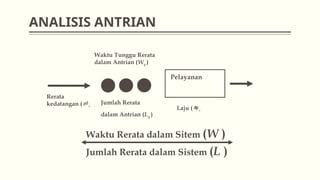
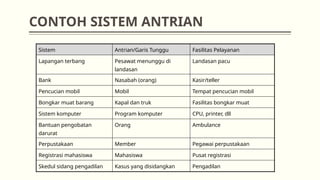
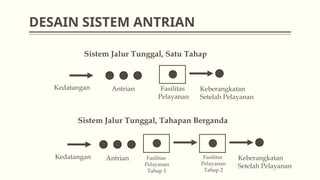
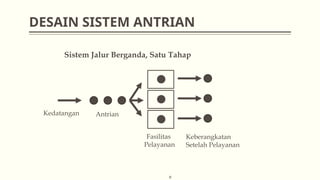
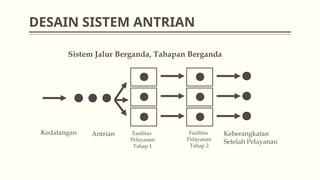
Dokumen ini membahas teori antrian dalam manajemen operasional, termasuk konsep dasar, analisis sistem, dan berbagai model antrian seperti m/m/1 dan m/m/s. Selain itu, dijelaskan juga berbagai aplikasi praktis dari teori antrian, seperti di rumah sakit dan pompa bensin. Contoh soal disertakan untuk menghitung tingkat intensitas layanan, jumlah rata-rata pelanggan, serta biaya terkait sistem antrian.

1. TEORI
ANTRIAN
Manajemen Operasional
Jurusan Manajemen, Fakultas Ekonomi,
Universitas Islam Malang (UNISMA)

2. ANTRIAN
Antrian timbul karena orang/sesuatu material/bahan tiba di
suatu fungsi service atau pelayanan/proses produksi lebih
cepat dibandingkan waktu mereka dilayani
Hal ini terjadi karena konsumen datang dalam rentang
waktu yang tidak tentu dan waktu pelayanan setiap
konsumen juga tidak konstan.
Sehingga antrian secara kontinuitas menjadi bertambah
dan berkurang panjangnya dan kadang-kadang kosong
dalam jangka panjang sesuai dengan frekuensi kedatangan
konsumen yang tidak tentu/acak (random).

3. STRUKTUR SISTEM ANTRIAN
Garis tunggu atau
antrian
Fasilitas
pelayanan
1
2
3
n
Sistem antrian
Pelanggan masuk
ke dalam sistem
antrian
Pelanggan keluar
dari sistem

4. ANALISIS ANTRIAN
Pelayanan
Rerata
kedatangan ( Jumlah Rerata
dalam Antrian (Lq )
Waktu Rerata dalam Sitem (W )
Jumlah Rerata dalam Sistem (L )
Waktu Tunggu Rerata
dalam Antrian (Wq )
Laju (

5. CONTOH SISTEM ANTRIAN
Sistem Antrian/Garis Tunggu Fasilitas Pelayanan
Lapangan terbang Pesawat menunggu di
landasan
Landasan pacu
Bank Nasabah (orang) Kasir/teller
Pencucian mobil Mobil Tempat pencucian mobil
Bongkar muat barang Kapal dan truk Fasilitas bongkar muat
Sistem komputer Program komputer CPU, printer, dll
Bantuan pengobatan
darurat
Orang Ambulance
Perpustakaan Member Pegawai perpustakaan
Registrasi mahasiswa Mahasiswa Pusat registrasi
Skedul sidang pengadilan Kasus yang disidangkan Pengadilan

6. KOMPONEN SISTEM ANTRIAN
 Ukuran Populasi Kedatangan
 Tak terbatas (essentially infinite)
 Terbatas (finite)
 Pola kedatangan pada sistem
 Terjadwal
 Secara acak  distribusi Poisson
 Disiplin pelayanan
 First Come First Served (FCFS)
 Shortest Processing Time (SPT)
 Priority (jobs are in different priority classes)
 Fasilitas pelayanan
 Single channel
 Multiple channel

7. DESAIN SISTEM ANTRIAN
Sistem Jalur Tunggal, Satu Tahap
Sistem Jalur Tunggal, Tahapan Berganda
Kedatangan Antrian Fasilitas
Pelayanan
Kedatangan Antrian Fasilitas
Pelayanan
Tahap 1
Fasilitas
Pelayanan
Tahap 2
Keberangkatan
Setelah Pelayanan
Keberangkatan
Setelah Pelayanan

8. DESAIN SISTEM ANTRIAN
8
Sistem Jalur Berganda, Satu Tahap
Kedatangan Antrian
Fasilitas
Pelayanan
Keberangkatan
Setelah Pelayanan

9. DESAIN SISTEM ANTRIAN
Sistem Jalur Berganda, Tahapan Berganda
Kedatangan Antrian Fasilitas
Pelayanan
Tahap 1
Fasilitas
Pelayanan
Tahap 2
Keberangkatan
Setelah Pelayanan

10. NOTASI DALAM ANALISIS SISTEM ANTRIAN
 n = Jumlah pelanggan dalam sistem. ‘
 Pn = Probabilitas kepastian n pelanggan dalam sistem.
 λ = Jumlah rata-rata pelanggan yang datang per satuan waktu.
 µ = Jumlah rata-rata pelanggan yang dilayani per satuan waktu.
 po = Probabilitas tidak ada pelanggan dalam sistem.
 P = Tingkat intensitas fasilitas pelayanan.
 L = Jumlah rata-rata pelangan yang diharapkan dalam sistem.
 Lq = Jumlah pelanggan yang diharapkan menunggu dalam antrian.
 W = Waktu yang diharapkan oleh pelanggan selama dalam sistem.
 Wq = Waktu yang diharapkan pelanggan selama menunggu dalam antrian.
 1/µ = Waktu rata-rata pelayanan.
 1A = Waktu rata-rata antar kedatangan.
 s = Jumlah fasilitas pelayanan.

11. MODEL ANTRIAN:
SINGLE CHANNEL MODEL (M/M/1)

12. ASUMSI M/M/1
 Populasi input tidak terbatas
 Distribusi kedatangan pelanggan potensial mengikuti distribusi
Poisson
 Disiplin pelayanan mengikuti pedoman FCFS
 Hanya ada satu fasilitas layanan dan Distribusi pelayanan
mengikuti distribusi Poisson (λ < μ)
 Kapasitas sistem diasumsikan tak terbatas
 Tidak ada penolakan maupun pengingkaran

13. RUMUS MODEL ANTRIAN M/M/1
Probabilitas bahwa pelayan sedang sibuk (yaitu, probabilitas seorang
pelanggan harus menunggu), dikenal dengan faktor utilisasi
Probabilitas tidak adanya pelanggan dalam suatu system antrian (baik
sedang dalam antrian maupun sedang dilayani) atau Probabilitas
bahwa pelayan menganggur
Probabilitas terdapat n pelanggan dalam suatu sistem antrian
Rata-rata jumlah pelanggan dalam suatu sistem antrian
Rata-rata jumlah pelanggan yang berada dalam baris antrian
Waktu rata-rata dihabiskan seorang pelanggan dalam keseluruhan
sistem antrian (yaitu, waktu menunggu dan dilayani)
Waktu rata-rata yang dihabiskan seorang pelanggan untuk menunggu
dalam antrian sampai dilayani
)
-
µ(µ
2



q
L
)
-
(µ 


L
0
.
µ
P
P
n
n








µ
-
1
P0













P
)
( 





q
W


L
W 


µ
1

14. CONTOH SOAL
Kasus Pompa Bensin (SPBU)
PT SGT mengoperasikan satu buah pompa bensin dengan satu orang
operator yang bernama John, Rata-rata tingkat kedatangan
kendaraan yaitu 20 kendaraan/mobil per jam. John dapat melayani
rata-rata 25 mobil per jam. Hitunglah soal-soal berikut ini untuk John:
 Tingkat intensitas (kegunaan) pelayanan (p).
 Jumlah rata-rata kendaraan yang diharapkan dalam sistem.
 Jumlah kendaraan yang diharapkan menunggu dalam antrian.
 Waktu yang diharapkan oleh setiap kendaraan selama dalam
sistem (menunggu pelayanan).
 Waktu yang diharapkan oleh setiap kendaraan untuk menunggu
dalam antrian.

15. Dari kasus SPBU, diketahui λ = 20 dan µ = 25
 Tingkat intensitas (kegunaan) pelayanan atau p
p = λ / μ = 20/25 = 0.80
Angka tersebut menunjukkan bahwa John akan sibuk melayani mobil
selama 80% dari waktunya. Sedangkan 20% dari waktunya atau (1 - p) atau
(1 - 0,80) yang sering disebut idle time akan digunakan John untuk istirahat,
membersihkan pompa dan lain-lain.
 Jumlah rata-rata kendaraan yang diharapkan dalam system (L)
L = λ / (μ – λ) = 20 / (25-20) = 4, atau
L = p / (1-p) = 0.80 / (1-0.80) = 4
Angka 4 menunjukkan bahwa John dapat mengharapkan 4 mobil yang
berada dalam sistem.
PENYELESAIAN

16. PENYELESAIAN
 Jumlah kendaraan yang diharapkan menunggu dalam antrian
Angka tersebut menunjukkan bahwa, mobil yang menunggu untuk dilayan
dalam antrian sebanyak 3 kendaraan.
 Waktu yang diharapkan oleh setiap kendaraan selama dalam sistem
(menunggu pelayanan)
W = 1 / (μ – λ) = 1 / (25-20) = 0.2 jam atau 12 menit
Angka tersebut menunjukkan bahwa, waktu rata-rata kendaraan menunggu
dalam sistem selama 12 menit.
 Waktu yang diharapkan oleh setiap kendaraan untuk menunggu dalam
antrian
Wq = λ / μ (μ – λ) = 20 / 25(25-20) = 0.16 jam atau 9.6 menit
Angka tersebut menunjukkan bahwa, waktu rata-rata kendaraan menunggu
dalam antrian selama 9,6 menit.
Lq = λ2
/ μ (μ – λ) = (20)2
/ 25(25-20) = 3.2 -- 3

17. MODEL ANTRIAN:
MULTI CHANNEL MODEL (M/M/S)

18. MULTI CHANNEL MODEL (M/M/s)
Dasar yang digunakan dalam multiple-channel model
adalah sistem (M/M/s). Perbedaannya dengan single-
channel model adalah terletak pada jumlah fasilitas
pelayanan. Dalam multiple-channel model, fasilitas
pelayanan yang dimiliki lebih dari satu. Huruf (s) yang
terdapat dalam sistem (M/M/s) menyatakan jumlah fasilitas
pelayanan.

19. ASUMSI M/M/s
 Populasi input tidak terbatas
 Distribusi kedatangan pelanggan potensial mengikuti
distribusi Poisson
 Disiplin pelayanan mengikuti pedoman FCFS
 Ada beberapa fasilitas pelayanan (S)
 Distribusi pelayanan mengikuti distribusi Poisson (λ < sμ)
 Kapasitas sistem diasumsikan tak terbatas
 Tidak ada penolakan maupun pengingkaran

20. RUMUS MODEL ANTRIAN M/M/s
Probabilitas seorang pelanggan yang datang
dalam sistem tersebut harus menunggu untuk
dilayani
Probabilitas tidak adanya pelanggan dalam
sistem tersebut
Probabilitas terdapat n pelanggan dalam sistem
antrian tersebut
Jumlah rata-rata pelanggan dalam
sistem antrian tersebut
Jumlah rata-rata pelanggan dalam antrian
tersebut
Waktu rata-rata yang dihabiskan pelanggan
dalam sistem antrian tersebut














































c
c
c
n
P
c
n
c
n
n
!
1
!
1
1
1
0
0
c
n
untuk
P
n
P
c
n
untuk
P
P
n
n
c
n
n
n
c
c

















 
1
;
1
,
0
,
0
! 



   









 0
2
!
1
)
/
(
P
c
c
c
L

L
W 



L
Lq


q
q
L
W
W 


1
0
!
1
P
c
c
c
P
c






 






21. CONTOH SOAL
Sebuah rumah sakit memiliki sebuah ruang gawat
darurat (RGD) yang berisi tiga bagian ruangan yang
terpisah untuk setiap kedatangan pasien. Setiap
ruangan memiliki satu orang dokter dan satu orang
jururawat. Secara rata-rata seorang dokter dan
jururawat dapat merawat 5 orang pasien per jam. A
Rata-rata tingkat kedatangan pasien yaitu 12 pasien
per jam. Dan diketahui Po = 0,20

22. PENYELESAIAN

23. Rata-rata pasien menunggu antrian selama 0,768*60 = 46 menit
Pasien menunggu dalam sistem selama 0,968*60 = 58 menit
Pihak rumah sakit mengharapkan 12 pasien berada di sistem
PENYELESAIAN

24. BIAYA MINIMUM ANTRIAN

25. MODEL BIAYA MINIMUM
 Persamaan biaya total per jam sebagai berikut:
TC = SC + WC
Keterangan:
TC : total biaya per jam,
SC : biaya pelayanan per jam,
WC : biaya menunggu per jam per pelanggan.
 Jika biaya menunggu per jam per pelanggan adalah Cw dan rata-rata pelanggan
menghabiskan waktunya: W jam dalam sistem, maka rata-rata biaya menunggu
per pelanggan adalah WCw. Jika tingkat rata-rata kedatangan pelanggan per jam
adalah λ, maka dengan persamaan L = λW, maka total biaya menunggu per jam
adalah:
WC = λ(WcW) = (λW)cw = Lcw
Cw
λ
-
μ
λ
LCw 

26. Masalah Bongkar Muat Barang
Sebuah perusahaan membeli bahan dari berbagai sumber. Bahan
diangkut dengan menggunakan truk dan rata-rata setiap hari
menerima kedatangan satu truk. Pembongkaran dilakukan oleh
sekelompok tenaga kerja baik langsung maupun tidak. Jumllah
minimal anggota kelompok kerja adalah 2 orang
 Kelompok tenaga kerja memiliki (n) anggota dan dapat
membongkar 0,8n truk per hari.
 Biaya yang harus dikeluarkan ketika truk ditahan karena sedang
melakukan pembongkaran sebesar Rp. 300.000,00. Setiap pekerja
yang bertugas melakukan pemuatan menerima upah sebesar Rp.
105.000,00 per hari.
 Tentukan jumlah optimum anggota kelompok kerja.
CONTOH SOAL

27. Model antrian yang digunakan adalah sistem (M/M/1) dengan λ = 1
truk per hari. Tingkat pelayanan µ = 0,8n, di mana n = jumlah anggota
kelompok kerja. Persoalannya adalah menentukan nilai n agar total
biaya per hari minimum.
 Jika terdapat n pekerja dalam satu kelompok, maka biaya pelayanan
adalah SC = 105.000n (Rp/hari). Maka biaya menunggu per hari: Cw =
300.000 (Rp/hari/truk),
 Persamaan total biaya:
1
-
0.8n
300.000
300.000
x
1
-
0.8n
1
LCw
1
-
0,8n
1
λ
-
μ
λ
L 




1
-
0,8n
300000
105.000n
WC
SC
TC 



PENYELESAIAN

28.  Persamaan total biaya di atas adalah total biaya per hari,
sedangkan TC adalah fungsi dari variabel (n). Oleh karena itu kita
harus menentukan (n) untuk meminimumkan TC. Dalam
pembahasan ditentukan bahwa paling sedikit menggunakan 2
pekerja dalam kelompok kerja.
 Jumlah tenaga kerja optimum dalam kelompok kerja adalah
sebanyak 3 orang pekerja, karena biaya paling rendah.
1
-
0,8n
300000
105.000n
TC 
 /hari
Rp.710.000
1
-
0,8(2)
300000
105.000(2)
TC 


/hari
Rp.529.285
1
-
0,8(3)
300000
105.000(3)
TC 


/hari
Rp.556.360
1
-
0,8(4)
300000
105.000(4)
TC 


PENYELESAIAN

29. Soal
Suatu rental komputer mempunyai tiga pengetik. Setiap pengetik
dapat mengetik rata-rata 6 surat/jam. Jika surat-surat yang masuk
rental tersebut sebanyak 15 surat/jam, tentukan:
1. Tingkat intensitas (kegunaan) pelayanan?
2. Jumlah rata-rata surat yang diharapkan dalam antrian?
3. Jumlah surat yang diharapkan menunggu dalam sistem?
4. Waktu yang diharapkan oleh setiap surat selama dalam antrian ?
5. Waktu yang diharapkan oleh setiap surat untuk menunggu dalam
sistem?