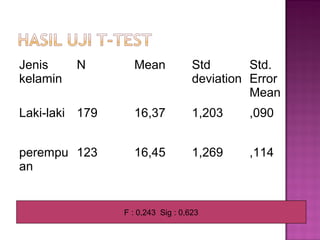
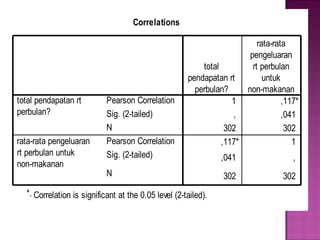
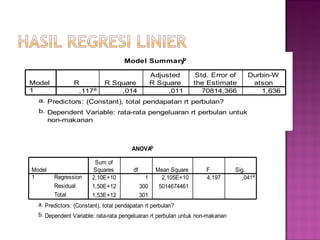
Dokumen ini membahas statistik parametrik dan non-parametrik serta uji hipotesis terkait perbedaan rata-rata umur laki-laki dan perempuan yang menunjukkan tidak ada perbedaan signifikan. Selain itu, terdapat analisis korelasi antara pendapatan rumah tangga dan pengeluaran untuk makanan, yang menunjukkan hubungan positif yang signifikan. Hasil analisis regresi menunjukkan bahwa sekitar 11% perubahan pengeluaran untuk makanan dipengaruhi oleh pendapatan.

1.  Statistik parametrik : mendasarkan pada
asumsi terhadap data yang akan
digunakan terutama menyangkut
distribusi data. Digunakan untuk data
interval dan rasio
 Statistik non-parametrik : normalitas
distribusi data biasanya hanya untuk data
interval atau rasio, sehingga untuk data
nominal dan ordinal digukan statistik non
parametrik

2.  Suatu data set yang dikomparasikan dapat
dikategorikan menjadi dua, yaitu related
dan unrelated
 Related : menggambarkan dua kondisi
pada populasi yang sama
 Contoh : pendapatan dan pendidikan
 Unrelated : menggambarkan dua kondisi
pada populasi yang berbeda.
 Contoh
: pendapatan antara laki-laki dan
perempuan

3.  Jumlah variabel yang akan digunakan dalam
analisis : univariate (1 variabel); bivariate (2
variabel) atau multivariate (lebih dari 2
variabel)
 Skala pengukuran
 Hipotesis yang akan diuji

4.  Pertanyaan : apakah terdapat perbedaan
yang nyata antara rata-rata umur laki-laki
dan perempuan
 Hipotesis alternatif: terdapat perbedaan
rata-rata umur laki-laki dan perempuan
secara signifikan
 Hipotesis null : tidak terdapat perbedaan
rata-rata umur laki-laki dan perempuan
 Alat uji : t-test

5. Jenis N Mean Std Std.
kelamin deviation Error
Mean
Laki-laki 179 16,37 1,203 ,090
perempu 123 16,45 1,269 ,114
an
F : 0,243 Sig : 0,623

6.  Hasil test menunjukkan bahwa rata-rata
umur laki-laki adalah 16,37 sementara
perempuan 16,45.
 Dengan tingkat kepercayaan (level of
confidence) 95 % atau 0,05 maka
perbedaan tersebut tidak signifikan.
 Hal itu dapat dilihat dari nilai sig. yang
lebih besar dari 0,05.
 Artinya hipotesis null diterima dan
hipotesis alternatif ditolak

7.  Pertanyaan : bagaimana hubungan antara
pendapatan rumah tangga dan pengeluaran
untuk makan ?
 Hipotesis alternatif : terdapat hubungan positif
antara pendapatan rumah tangga dengan
pengeeluaran untuk makan. Semakin besar
pendapatan rumah tangga semakin besar
pengeluaran untuk makanan
 Hipotesis null : tidak ada hubungan antara
pendapatan rumah tangga dengan pengeluaran
untuk makanan.
 Alat uji : Korelasi produk moment

8. Correlations
rata-rata
pengeluaran
total rt perbulan
pendapatan rt untuk
perbulan? non-makanan
total pendapatan rt Pearson Correlation 1 ,117*
perbulan? Sig. (2-tailed) , ,041
N 302 302
rata-rata pengeluaran Pearson Correlation ,117* 1
rt perbulan untuk Sig. (2-tailed) ,041 ,
non-makanan
N 302 302
*. Correlation is significant at the 0.05 level (2-tailed).

9.  Hasil uji korelasi menunjukkan bahwa nilai
korelasinya adalh 0,114
 Angka ini signifikan pada derajat
kepercayaan 95 %
 Artinya : hipotesis null ditolak atau hipotesis
alternatif diterima. Terbukti bahwa semakin
besar pendapatan rumah tangga semakin
besar pengeluaran untuk makanan

10.  Hasil korelasi hanya menunjukkan hubungan,
tetapi belum dapat menjawab apakah
pendapatan mempengaruhi pengeluaran
untuk makanan
 Uji pengaruh IV thd DV jika keduanya dalam
skala pengukuran interval atau rasio, maka
dapat digunakan least linier regression
(pearson product moment)

11. b
Model Summary
Adjusted Std. Error of Durbin-W
Model R R Square R Square the Estimate atson
1 ,117a ,014 ,011 70814,366 1,636
a. Predictors: (Constant), total pendapatan rt perbulan?
b. Dependent Variable: rata-rata pengeluaran rt perbulan untuk
non-makanan
ANOVAb
Sum of
Model Squares df Mean Square F Sig.
1 Regression 2,10E+10 1 2,105E+10 4,197 ,041a
Residual 1,50E+12 300 5014674461
Total 1,53E+12 301
a. Predictors: (Constant), total pendapatan rt perbulan?
b. Dependent Variable: rata-rata pengeluaran rt perbulan untuk non-makanan

12.  Tabel ke 2 memperlihatkan bahwa nilai
sig. adalah 0,041 (lihat hasil nilai sig pada
uji korelasi)
 Seberapa besar kontribusi IV terhadap
perubahan DV dapat dilihat dari nilai
agjusted R square (0,11) artinya adalah
perubahan pengeluaran untuk makanan 11
persen dipengaruhi oleh besarnya
pendapatan
 Persamaan y = a + bx dapat dijabarkan
dengan melihat nilai b ----- y = 53675,5 +
0,025 x