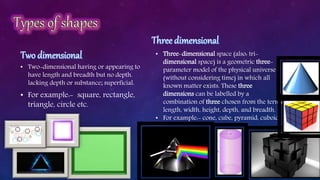
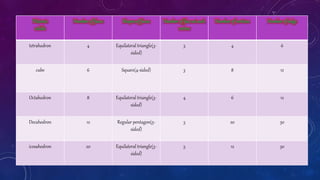
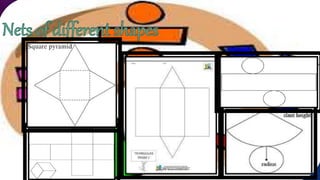
A polyhedron is a three-dimensional solid shape bounded by flat polygons. It has faces, edges, and vertices. Faces are the flat polygons that make up the sides of the polyhedron. Edges are the lines where faces meet. Vertices are the points where edges intersect. Regular polyhedra have identical regular polygons for faces and the same number of faces meeting at each vertex. Prisms and pyramids are examples of polyhedra. Euler's formula relates the number of faces, edges and vertices of any polyhedron as F + V = E + 2.

3. shape

4. • Two-dimensional having or appearing to
have length and breadth but no depth.
lacking depth or substance; superficial.
• For example:- square, rectangle,
triangle, circle etc.
• Three-dimensional space (also: tri-
dimensional space) is a geometric three-
parameter model of the physical universe
(without considering time) in which all
known matter exists. These three
dimensions can be labelled by a
combination of three chosen from the terms
length, width, height, depth, and breadth.
• For example:- cone, cube, pyramid, cuboid.

5. The word Polyhedra is the plural of word polyhedron which may be defined
as follows:
Polyhedron a solid shape bounded by polygons is called a polyhedron.
 Faces polygons forming a polyhedron are know as its faces.
 edges lines segment common to intersecting faces of a polyhedron are
know as its edges.
 Vertices points of intersecting of edges of a polyhedron are know as its
vertices.
In a polyhedron three or more edges meet at a point to form a
vertex.

6. Polyhedron: A polyhedron is a three-dimensional solid figure in which each
side is a flat surface. These flat surfaces are polygons and are joined at their
edges. The word polyhedron is derived from the Greek poly (meaning many)
and the Indo-European hedron (meaning seat or face).
Non polyhedron: spheres, cones and cylinders are a few example of non
polyhedron.
Euler's Polyhedron Theorem:
Euler discovered that the number of faces (flat surfaces) plus the number
of vertices (corner points) of a polyhedron equals the number of edges of the
polyhedron plus 2.
F + V = E + 2

7. POLYHEDRONS
i. Cuboid iv. Triangular pyramid or tetrahedron
F = number of faces = 6 F = number of faces = 4
E = number of edges = 12 E = number of edges = 6
V = number of vertices = 8 V = number of vertices = 4
ii. Cube v. Triangular prism
F = number of faces = 6 F = number of faces = 5
E = number of edges = 12 E = number of edges = 9
V = number of vertices = 8 V = number of vertices = 6
iii. Pyramid
F = number of faces = 5
E = number of edges = 8
V = number of vertices = 5

9. In a convex polyhedron , the fine segment joining any two points
on the surface of polyhedron lies entirely inside or on the
polyhedron.
A polyhedron some of whose plane section are concave polygons
is known as a concave polyhedron. Concave polygons have at
least one interior angle greater than 180* and has some of its side
inward

10. A polyhedron is said to be regular if its faces are made up
of regular polygons and the same number of faces meet at
each vertex. An irregular polyhedron is made up of
polygons whose sides and angles are not of equal measures

11. Prisms: a glass or other transparent object in the form of a prism, especially one that is
triangular with refracting surfaces at an acute angle with each other and that
separates white light into a spectrum of colours.
Pyramids: In geometry, a pyramid is a polyhedron formed by connecting
a polygonal base and a point, called the apex. Each base edge and apex form a triangle,
called a lateral face. It is a conic solid with polygonal base. A pyramid with an n-sided
base will have n + 1 vertices, n + 1 faces, and 2n edges. All pyramids are self-dual.

12. Platonic
solids
Number of faces Shapesof faces Number of face at each
vertex
Number of vertices Number of edge
tetrahedron 4 Equilateral triangle(3-
sided)
3 4 6
cube 6 Square(4-sided) 3 8 12
Octahedron 8 Equilateral triangle(3-
sided)
4 6 12
Decahedron 12 Regular pentagon(5-
sided)
3 20 30
icosahedron 20 Equilateral triangle(3-
sided)
5 12 30

13. A pattern that you can cut and fold to make
a model of a solid shape.
Like net of a cube, cuboid, prism etc.
Also means what is left after all deductions
have been made.

15. Q1. What is the least number of planes that can enclose a solid? what is the name of
the solid?
Q2. Is a square prism as a cube?
Q3. Can a polyhedron have 10 faces, 20 edges and 15 vertices?
Q4. Is it possible to have polyhedron with any given number faces?
Q5. Using Euler's formula find the unknown:
Q6. Draw net of:
faces ? 5 20
vertices 6 ? 12
edges 12 9 ?

16. A1. number of planes- 4
shape – tetrahedron
A2. yes
A3. no
A4. yes, if number of faces is four or more
A5. i) faces 8 ii) vertices 6 ii) edges 30
A 6