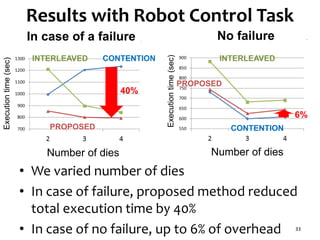
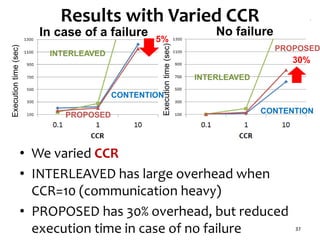
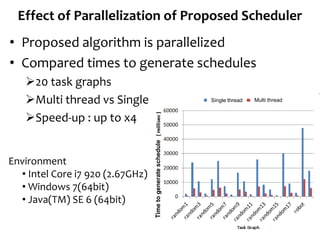
The document presents a task scheduling algorithm designed for multicore processors to minimize recovery time in case of a single node failure. It introduces a new scheduling method that accounts for network contention and multicore processor failure, aiming to improve upon existing methods that overlook these factors. Testing results show that the proposed method significantly reduces execution time during failures by optimizing task distribution across processor dies.

1. Task scheduling algorithm for multicore
processor system for minimizing recovery
time in case of single node fault
1
Shohei Gotoda†, Naoki Shibata‡, Minoru Ito†
†Nara Institute of Science and Technology
‡Shiga University

2. Background
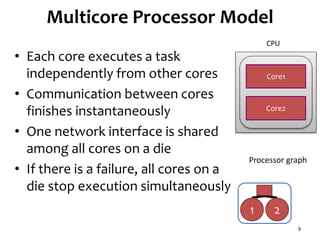
• Multicore processors
 Almost all processors designed recently are
multicore processors
• Computing cluster consisting of 1800 nodes
experiences about 1000 failures[1]
in the first year after deployment
[1] Google spotlights data center inner workings
cnet.com article on May 30, 2008

3. Objective of Research
• Fault tolerance
 We assume a single fail-stop failure of a multicore
processor
• Network contention
 To generate schedules reproducible on real
systems
3
Devise new scheduling method that
minimizes recovery time
taking account of the above points

4. Task Graph
• A group of tasks that can be
executed in parallel
• Vertex (task node)
Task to be executed on a single
CPU core
• Edge (task link)
Data dependence between tasks
4
Task node Task link
Task graph

5. Processor Graph
• Topology of the computer network
• Vertex (Processor node)
CPU core (circle)
• has only one link
Switch (rectangle)
• has more than 2 links
• Edge (Processor link)
Communication path between
processors
5
Processor node Processor linkSwitch
Processor graph
321

6. Task Scheduling
• Task scheduling problem
 assigns a processor node to each
task node
 minimizes total execution time
An NP-hard problem
6
1
One processor node is
assigned to each task node
321
Processor graph
Task graph

7. Inputs and Outputs for Task Scheduling
• Inputs
Task graph and processor graph
• Output
A schedule
• which is an assignment of a processor
node to each task node
• Objective function
Minimize task execution time
7
3
31
31
321
Processor graph
Task graph

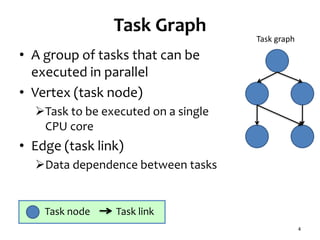
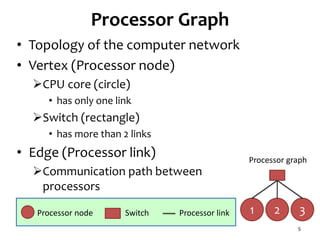
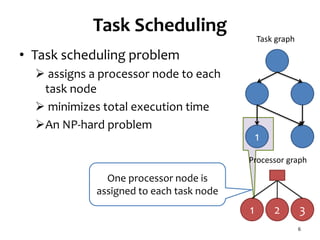
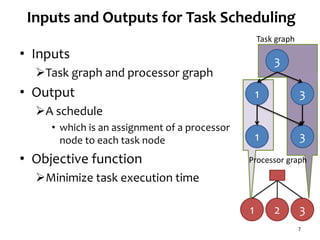
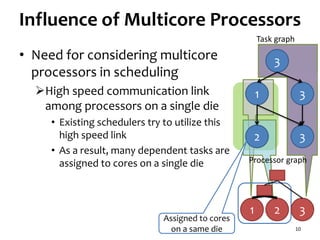
8. Network Contention Model
• Communication delay
If processor link is occupied by another
communication
• We use existing network contention
model[2]
8
3
31
32
Contention 321
Processor graph
Task graph
[2] O. Sinnen and L.A. Sousa, “Communication Contention in
Task Scheduling,“ IEEE Trans. Parallel and Distributed Systems,
vol. 16, no. 6, pp. 503-515, 2005.

9. Multicore Processor Model
• Each core executes a task
independently from other cores
• Communication between cores
finishes instantaneously
• One network interface is shared
among all cores on a die
• If there is a failure, all cores on a
die stop execution simultaneously
9
Core1
Core2
CPU
21
Processor graph

10. Influence of Multicore Processors
10
• Need for considering multicore
processors in scheduling
High speed communication link
among processors on a single die
• Existing schedulers try to utilize this
high speed link
• As a result, many dependent tasks are
assigned to cores on a single die
3
31
32
321
Assigned to cores
on a same die
Processor graph
Task graph

11. • Need for considering multicore
processors in scheduling
High speed communication link
among processors on a single die
• Existing schedulers try to utilize this
high speed link
• As a result, many dependent tasks are
assigned to cores on a single die
In case of fault
• Dependent tasks tends to be
destroyed at a time
11
3
31
32
321
Processor graph
Task graph
Influence of Multicore Processors
Assigned to cores
on a same die

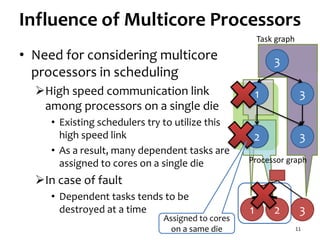
12. Related Work (1/2)
• Checkpointing [3]
Node state is saved in each node
Backup node is allocated
Recover processing results from saved state
Multicore is not considered
Network contention is not considered
12
[3] Y. Gu, Z. Zhang, F. Ye, H. Yang, M. Kim, H. Lei, and Z. Liu. An empirical study of high
availability in stream processing systems. In Middleware ’09: the 10th
ACM/IFIP/USENIX International Conference on Middleware (Industrial Track), 2009.
1
2
3
4
Input
Queue
Output
Queue
Secondary
Primary
Backup

13. Related Work (2/2)
• Task scheduling method[5] in which
 Multiple task graph templates are prepared
beforehand,
 Processors are assigned according to the templates
• This method is suitable for highly loaded
systems
[5] Wolf, J., et al.: SODA: An Optimizing Scheduler for Large-
Scale Stream-Based Distributed Computer Systems. In: ACM
Middleware (2008)

14. Our Contribution
• There is no existing method for scheduling
that takes account of both
• multicore processor failure
• network contention
• We propose a scheduling method taking
account of network contention and
multicore processor failure
14

15. Assumptions
• Only a single fail-stop failure of a multicore
processor can occur
Failed computing node automatically restart after
30 sec.
• Failure can be detected in one second
by interruption of heartbeat signals
• Use checkpointing technique to recover from
saved state
• Network contention
Contention model is same as the Sinnen’s model
15

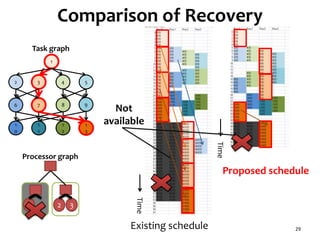
16. Checkpointing and Recovery
• Each processor node saves state to the main memory
when each task is finished
 Saved state is the data transferred to the succeeding processor
nodes
 Only output data from each task node is saved as a state
• This is much smaller than the complete memory image
 We assume saving state finishes instantaneously
• Since this is just copying small data within memory
• Recovery
 Saved state which is not affected by the failure is found in the
ancestor task nodes.
Some tasks are executed again using the saved state
16
[3] Y. Gu, Z. Zhang, F. Ye, H. Yang, M. Kim, H. Lei, and Z. Liu. An empirical study of high
availability in stream processing systems. In Middleware ’09: the 10th
ACM/IFIP/USENIX International Conference on Middleware (Industrial Track), 2009.

17. What Proposed Method Tries to Do
• Reduce recovery time in case of failure
 Minimizes the worst case total execution time
• Worst case in the all possible patterns of failure
• Each of dies can fail
 Execution time before failure + recovery

18. Worst Case Scenario
• Critical path
Path in task graph from first to last task with longest
execution time
• The worst case scenario
All tasks in critical path are assigned
to processors on a die
Failure happens when the last task is
being executed
We need two times of total execution time
18
Example task graph
First
Last

19. Idea of Proposed Method
• We distribute tasks on critical path over dies
But, there is communication overhead
If we distribute too many tasks, there is too much
overhead
• Usually, the last tasks in critical path have larger
influence
We check tasks from the last task in the critical path
We find the last k tasks in the critical path to other dies
We find the best k

20. Problem with Existing Method
20
1 2
3
A B C
21
3
BA
Resulting execution
Existing
Schedule
D
DC
• Task 1 is assigned to core A
• Task 2 is assigned to core B
• Task 3 is assigned to same die
• because of high
communication speed
Time

21. • Suppose that failure happens
when Task 3 is being executed
• All results are lost
21
1 2
3
A B C
21
3
BA
D
DC
Resulting execution
Existing
Schedule
Time
Problem with Existing Method

22. Problem with Existing Method
22
1 2
3
A B C
21
3
BA
D
DC
1’ 2’
3’
21
3
Resulting execution
Existing
Schedule
Time
• Suppose that failure happens
when Task 3 is being executed
• All results are lost
• We need to execute all tasks
again from the beginning
on another die

23. Improvement in Proposed Method
• Distribute influential tasks to
other dies
In this case, task 3 is the most
influential
23
21
3
Proposed schedule
1 2
3
A B C
BA
Resulting execution
D
DC
Comm.
overhead
Time

24. Recovery in Proposed Method
• Suppose that failure happens
when Task 3 is being executed
• Results of Task 1 and 2 are saved
24
21
3
1 2
3
A B C
BA
D
DC
Resulting execution
Time
Proposed schedule

25. Recovery in Proposed Method
• Suppose that failure happens
when Task 3 is being executed
• Results of Task 1 and 2 are saved
• Execution can be continued from
the saved state
25
3’
21
3
1 2
3
A B C
BA
D
DC
3
Resulting execution
Time
Proposed schedule

26. Communication Overhead
• Communication overhead is imposed to the
proposed method
26
Existing schedule Proposed schedule
overhead
1 2
3
A B C D
1 2
3
A B C D
Time

27. Speed-up in Recovery
27
Recovery with
existing schedule
Recovery with
proposed schedule
Proposed method has larger effect
if computation time is longer than
communication time
1 2
3
A B C D
1 2
3
A B C D
1’ 2’
3’
3’
speed-up
時間

28. Comparison of Schedules
28
Existing schedule Proposed schedule
Time
Time
Task graph
10 32
Processor graph
1
2
6 7
3 4
8 9
5
1
0
1
1
1
2
1
3

29. 29
Not
available
Comparison of Recovery
Existing schedule
Proposed schedule
Time
Time
Task graph
10 32
Processor graph
1
2
6 7
3 4
8 9
5
1
0
1
1
1
2
1
3

30. Evaluation
• Items to compare
Recovery time in case of a failure
Overhead in case of no failure
• Compared methods
PROPOSED
CONTENTION
• Sinnen’s method considering network contention
INTERLEAVED
• Scheduling algorithm that tries to spread tasks to all
dies as much as possible
30

31. Test Environment
• Devices
4 PCs with
• Intel Core i7 920 (2.67GHz) (Quad core)
• Intel Network Interface Card
 Intel Gigabit CT Desktop Adaptor (PCI Express x1)
• 6.0GB Memory
• Program to measure execution time
• Windows 7(64bit)
• Java(TM) SE Runtime Environment (64bit)
• Standard TCP socket
31

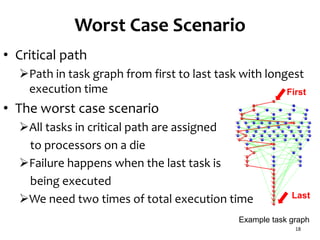
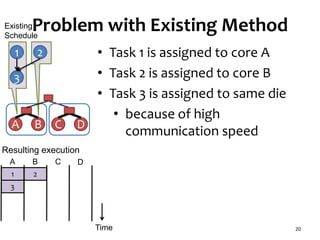
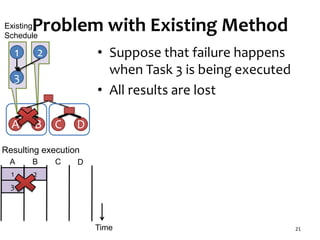
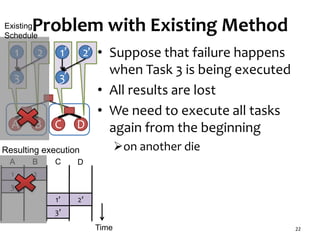
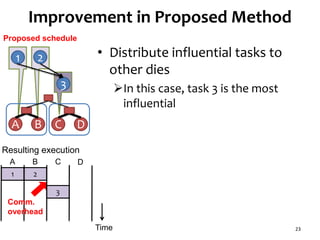
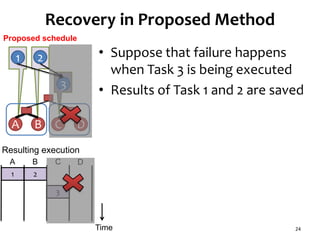
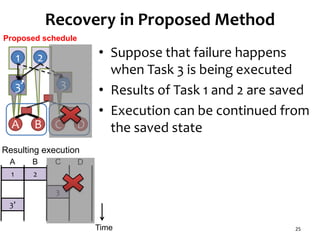
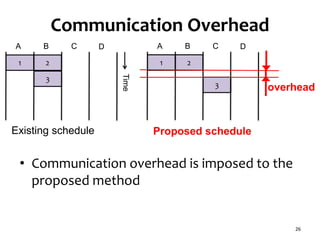
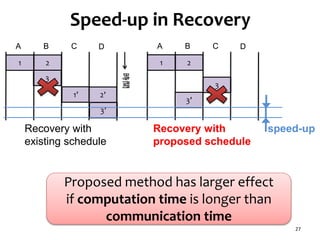
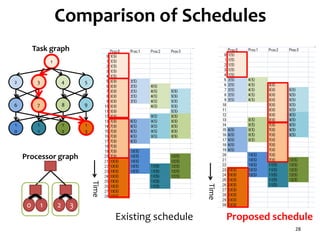
32. Task Graph with Low Parallelism
Configuration
• Number of task nodes：90
• Number of cores on a die：2
• Number of dies：2～4
• Robot control [4]
32
Task graph
Processor graph
10
Die
1 Core
Switch
4 5
Die
# of dies
32
Die
6 7
Die
[4] Standard Task Graph Set
http://www.kasahara.elec.waseda.ac.jp/schedule/index.html

33. Results with Robot Control Task
• We varied number of dies
• In case of failure, proposed method reduced
total execution time by 40%
• In case of no failure, up to 6% of overhead 33
In case of a failure No failure
40%
6%
Number of dies Number of dies
CONTENTIONINTERLEAVED
PROPOSED
INTERLEAVED
CONTENTION
PROPOSED
Executiontime(sec)
Executiontime(sec)

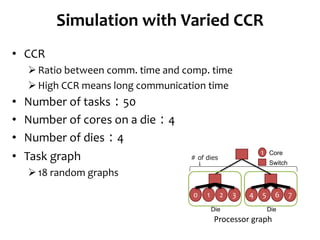
34. Configuration
• Number of task nodes：98
• Number of cores on a die：4
• Number of dies：2～4
• Sparse matrix solver [4]
34
10
Die
1 Core
Switch
2 3 54
Die
6 7
# of dies
Task Graph with High Parallelism
Processor graph
Task graph
[4] Standard Task Graph Set
http://www.kasahara.elec.waseda.ac.jp/schedule/index.html

35. Results with Sparse Matrix Solver
• We varied number of dies
• In case of failure, execution time including
recovery reduced by up to 25%
• In case of no failure, up to 7% of overhead 35
25%
7%
In case of a failure No failure
INTERLEAVEDINTERLEAVED
CONTENTION
CONTENTION
PROPOSED
PROPOSED
Number of diesNumber of dies
Executiontime(sec)
Executiontime(sec)

36. Simulation with Varied CCR
• CCR
Ratio between comm. time and comp. time
High CCR means long communication time
• Number of tasks：50
• Number of cores on a die：4
• Number of dies：4
• Task graph
18 random graphs
10
Die
1 Core
Switch
2 3 54
Die
6 7
# of dies
Processor graph

37. • We varied CCR
• INTERLEAVED has large overhead when
CCR=10 (communication heavy)
• PROPOSED has 30% overhead, but reduced
execution time in case of no failure 37
5%
30%
Results with Varied CCR
In case of a failure No failure
Executiontime(sec)
Executiontime(sec)
INTERLEAVED
CONTENTION
PROPOSED CONTENTION
PROPOSED
INTERLEAVED

38. Effect of Parallelization of Proposed Scheduler
• Proposed algorithm is parallelized
• Compared times to generate schedules
20 task graphs
Multi thread vs Single Thread
Speed-up : up to x4
38
Environment
• Intel Core i7 920 (2.67GHz)
• Windows 7(64bit)
• Java(TM) SE 6 (64bit)
Single thread Multi thread
Timetogenerateschedule

39. Conclusion
• Proposed task scheduling method considering
Network contention
Single fail-stop failure
Multicore processor
• Future work
Evaluation on larger computer system
39

40. Shohei Gotoda, Naoki Shibata and Minoru Ito :
"Task scheduling algorithm for multicore
processor system for minimizing recovery time
in case of single node fault," Proceedings of
IEEE International Symposium on Cluster
Computing and the Grid (CCGrid 2012), pp.260-
26, 2012.
DOI:10.1109/CCGrid.2012.23 [ PDF ]
40