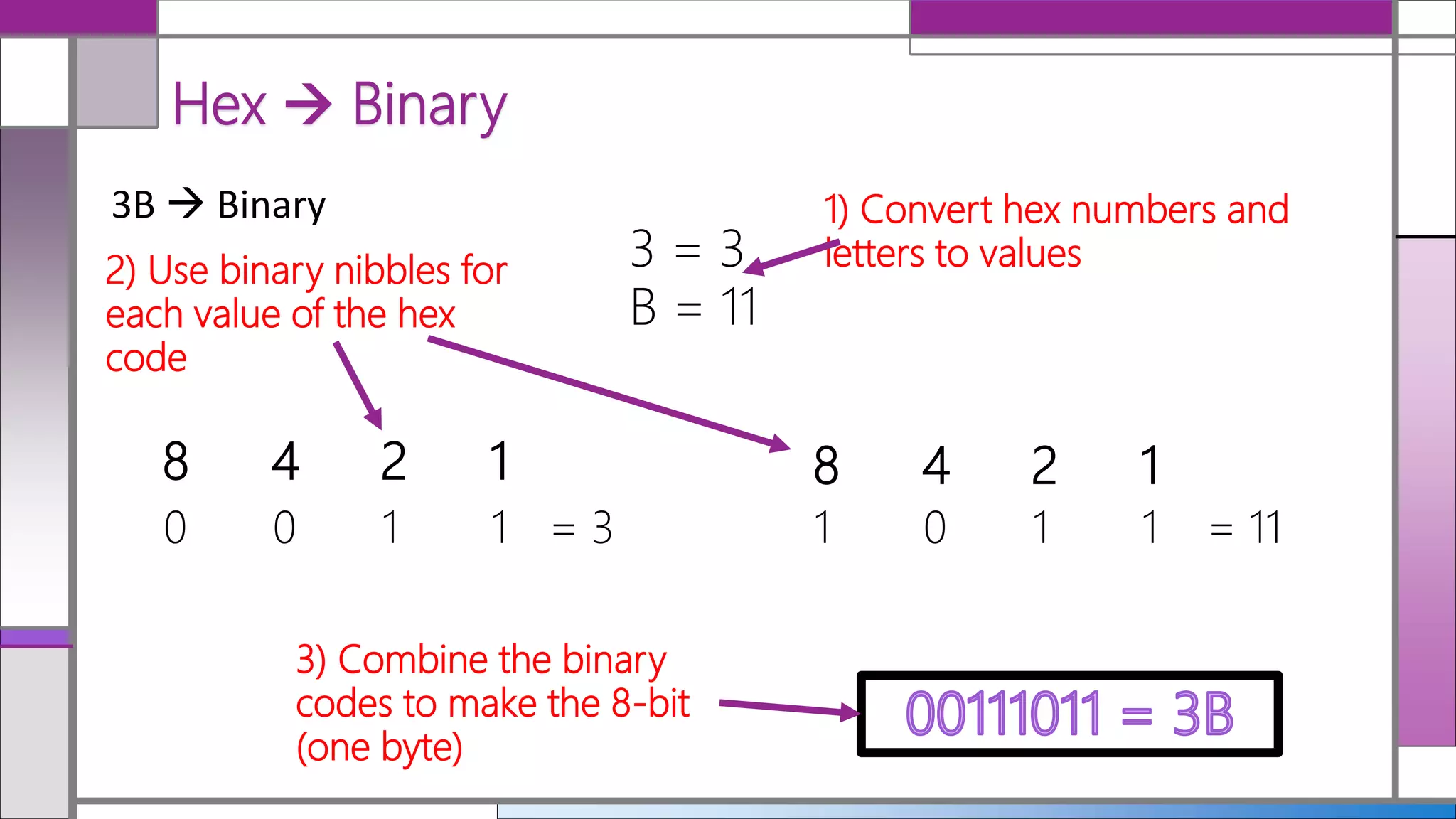
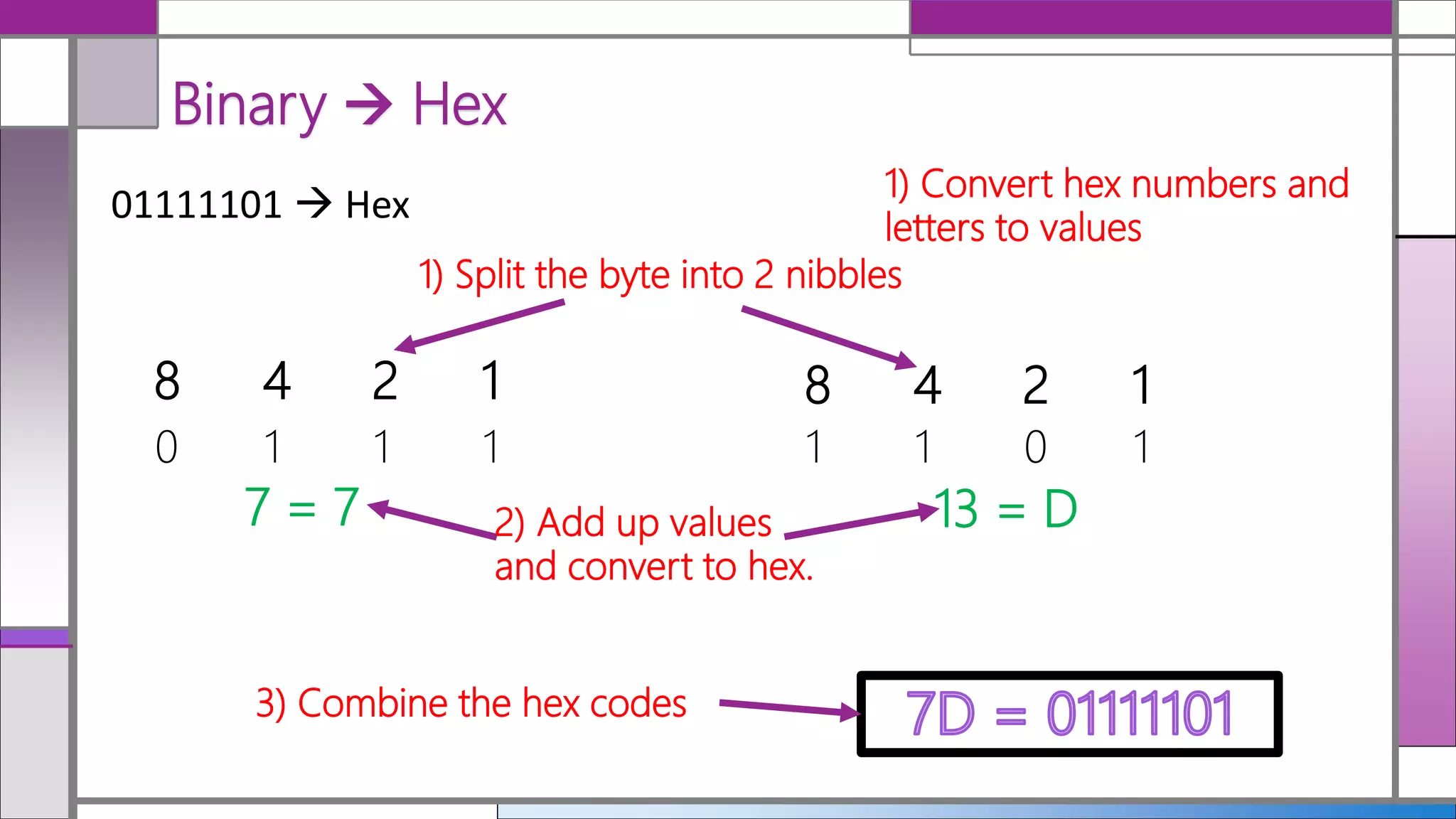
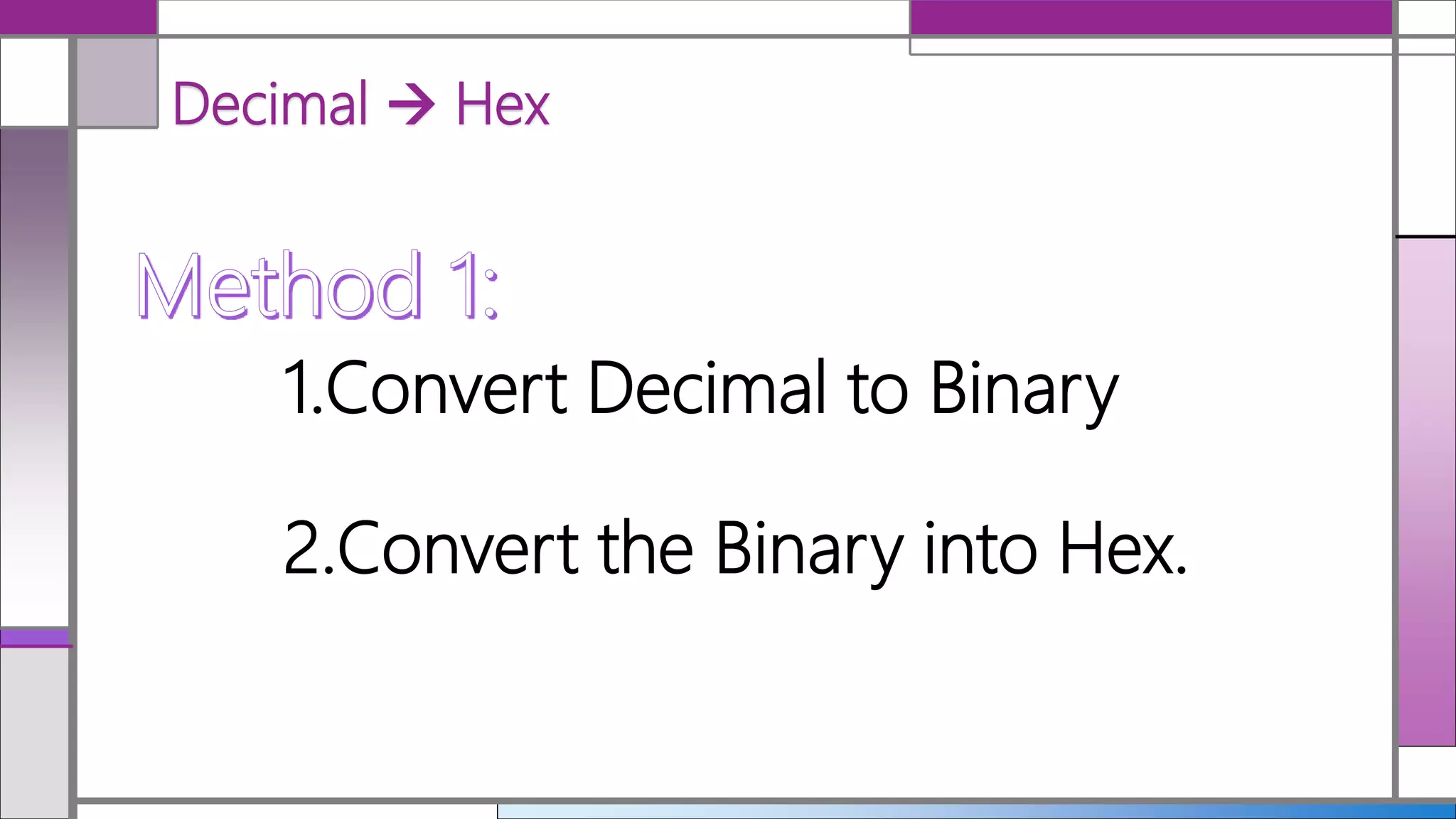
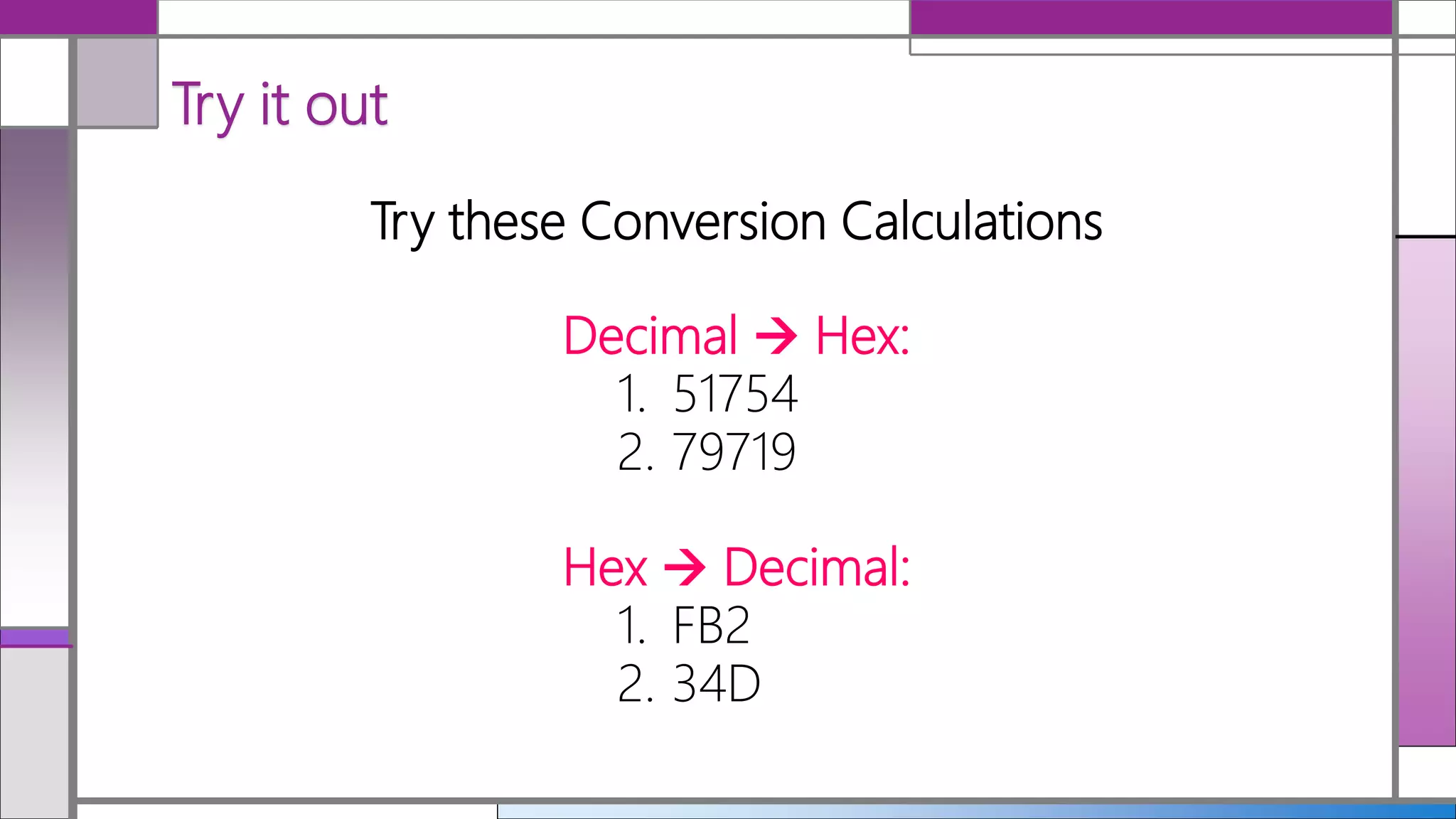
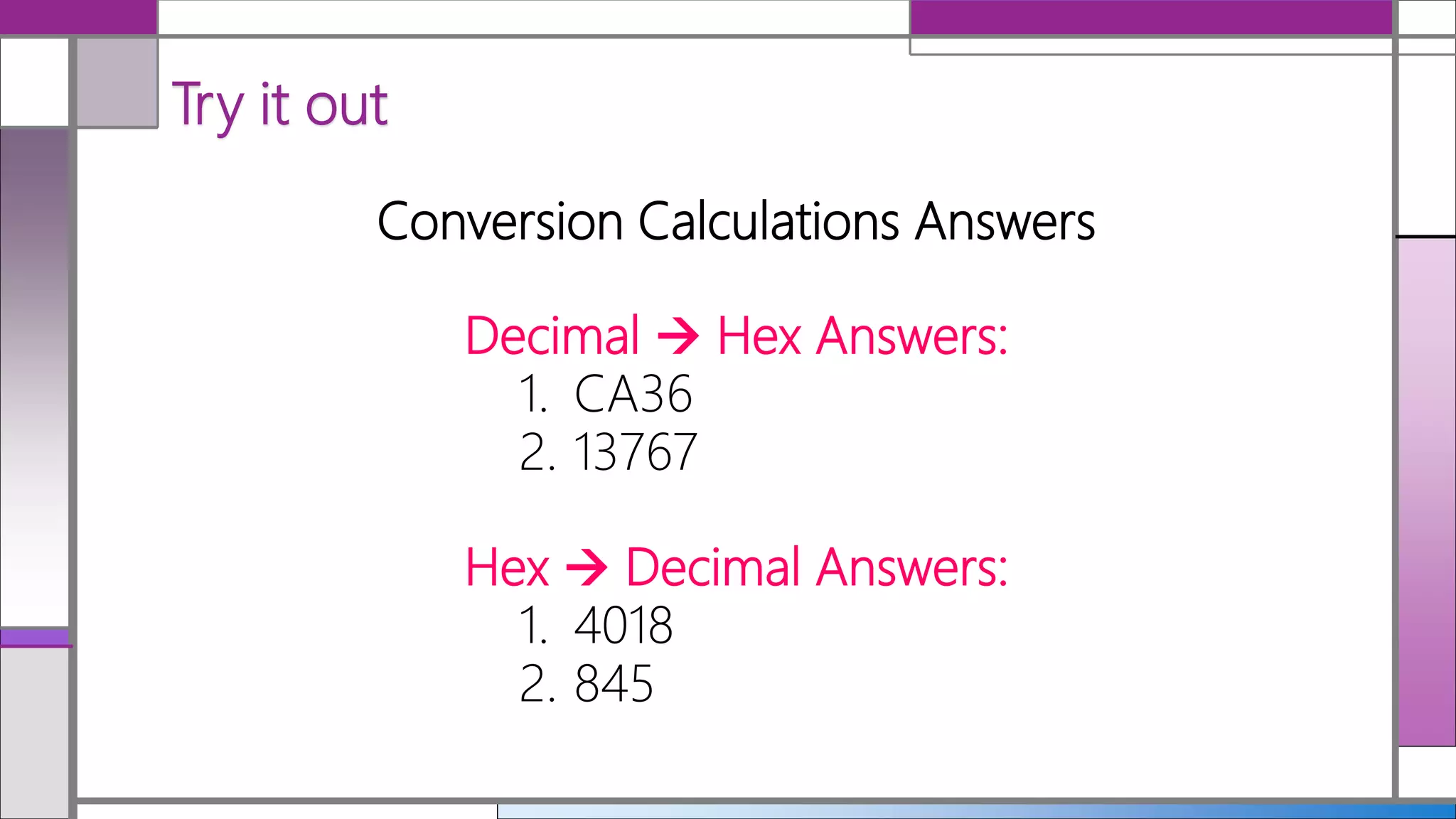
Hexadecimal (hex) is a base-16 numbering system that simplifies the representation of binary numbers, making them shorter and easier to read. Conversion between decimal, hex, and binary is detailed, with methods for translating hex to decimal and vice versa provided. The document includes examples and practice calculations to reinforce understanding of these conversions.

1. Computer Science
(A Level)
Hexadecimal

2. Hexadecimal (hex) is particularly useful for representing
large numbers as fewer digits are required.
An 8-bit binary code (one byte) can be represented as a
2-digit code in hex. Therefore, hex is ‘shorthand’ for
binary
Hexadecimal
Hex Values:
1-9, A-F
(1,2,3,4,5,6,7,8,9,A,B,C,D,E,F)

3. Hexadecimal
Why use hex instead of binary?
• Shorter
• Easier to read/write/remember
• Less mistakes
Hexadecimal N-bits:
Maximum value = 16ⁿˉ¹
Maximum Combos = 16ⁿ
Hexadecimal
= Base 16

4. 3B  Binary
Hex  Binary
3 = 3
B = 11
1) Convert hex numbers and
letters to values
8 4 2 1 8 4 2 1
2) Use binary nibbles for
each value of the hex
code
0 0 1 1 1 0 1 1= 3 = 11
3) Combine the binary
codes to make the 8-bit
(one byte)

5. 01111101  Hex
Binary  Hex
1) Convert hex numbers and
letters to values
8 4 2 1 8 4 2 1
1) Split the byte into 2 nibbles
0 1 1 1 1 1 0 1
3) Combine the hex codes
7 = 7 13 = D2) Add up values
and convert to hex.

6. Decimal  Hex
1.Convert Decimal to Binary
2.Convert the Binary into Hex.

7. Decimal  Hex
(1,048,576) (65, 536) 16³ (4096) 16² (256) 16¹ (16)
3571  Hex.
1)Draw out hex table
3571 ÷ 256 = 13 = D
2) Divide the number by the biggest number in the
table possible. (don’t count remainders)
3571 – (256 x 13) = 243
3) Subtract the product of the answer and
number from the table from the original
number
243 ÷ 16 = 15 = F
243 – (16 x 15) = 3
4) Carry on using this method until the answer
is too small
= Hex Answer

8. Hex  Decimal
2A3  Decimal
1) Covert the hex into numbers and
then into binary by splitting them into
individual nibbles
8 4 2 1 8 4 2 18 4 2 1
0 0 1 0 0 0 1 11 0 1 0
2 3A
2A3 = 001010100011
512 256 128 64 32 16 8 4 2 1
1 0 1 0 1 0 0 0 1 1
512 + 128 + 32 + 2 + 1 = 675
2) Covert Binary to Decimal

9. Try it out
Try these Conversion Calculations
Decimal  Hex:
1. 51754
2. 79719
Hex  Decimal:
1. FB2
2. 34D

10. Try it out
Conversion Calculations Answers
Decimal  Hex Answers:
1. CA36
2. 13767
Hex  Decimal Answers:
1. 4018
2. 845