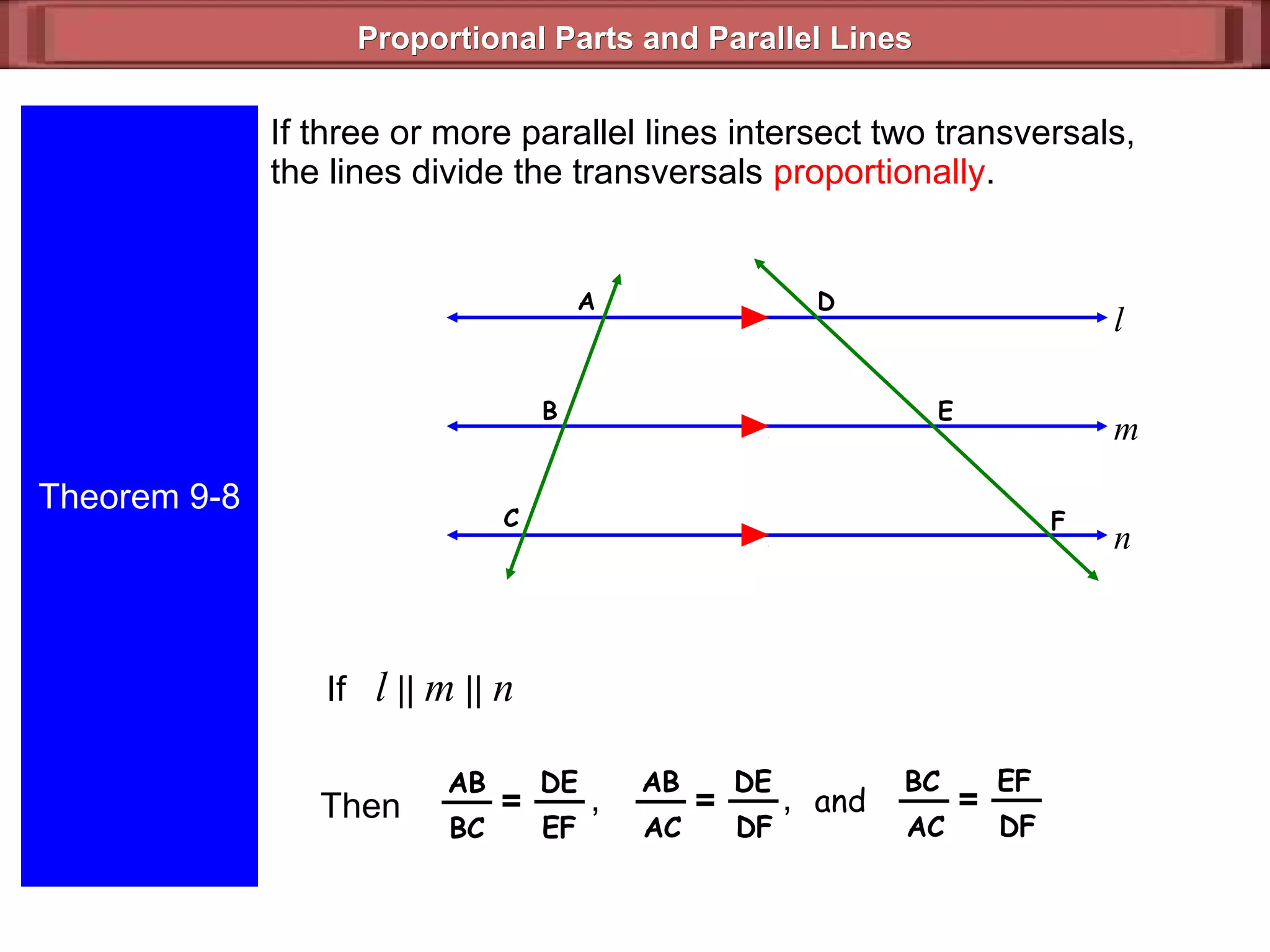
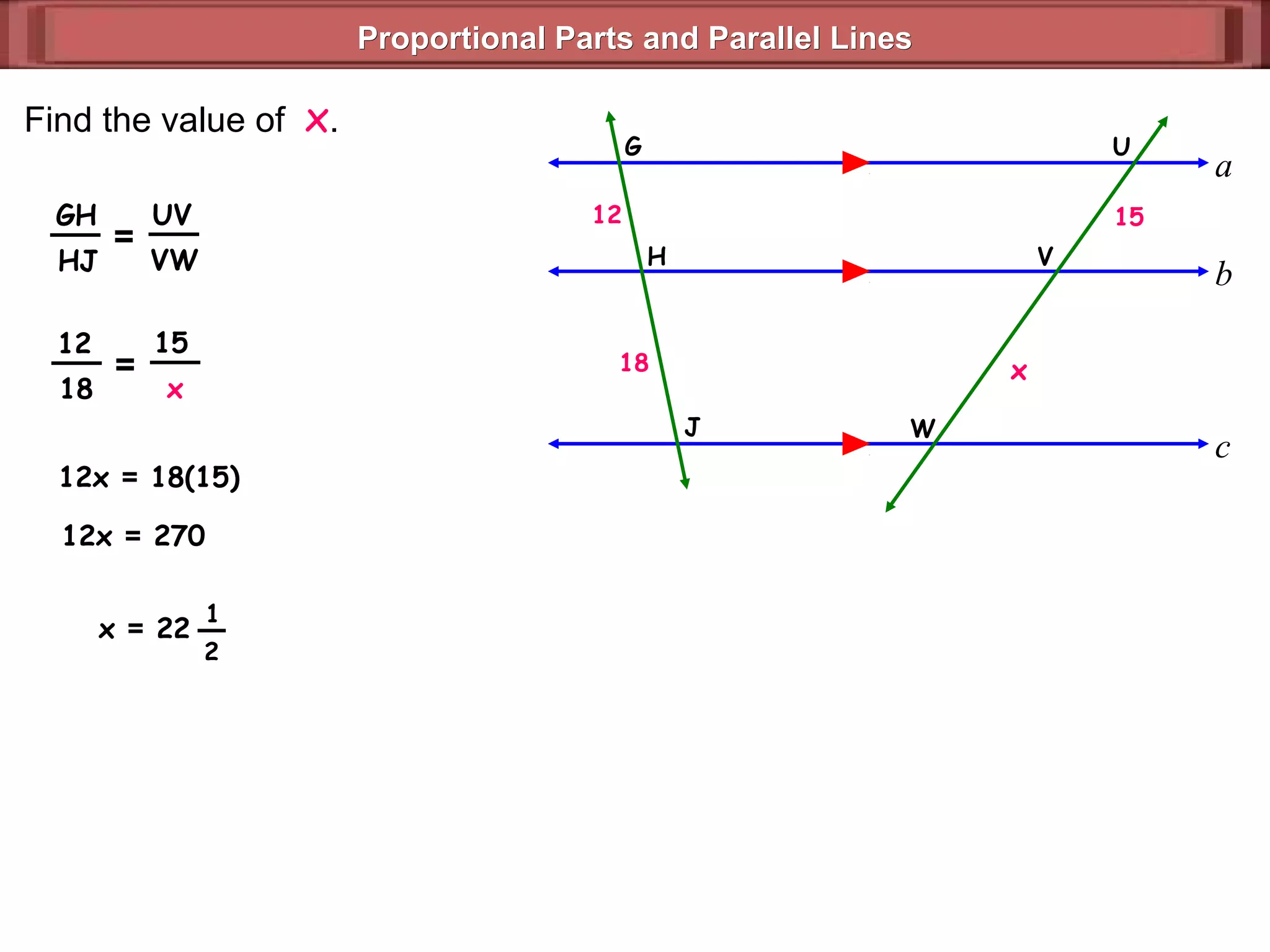
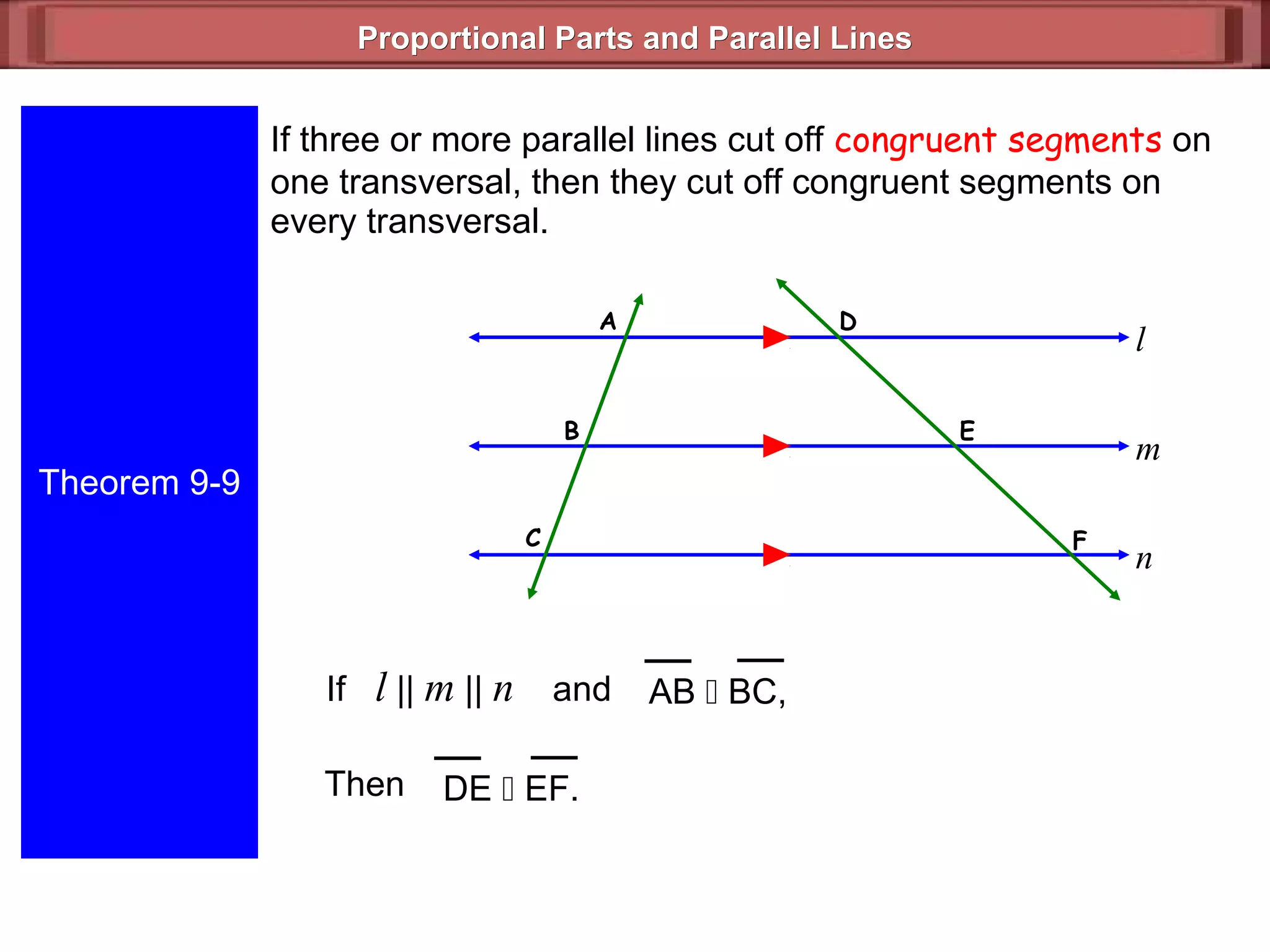
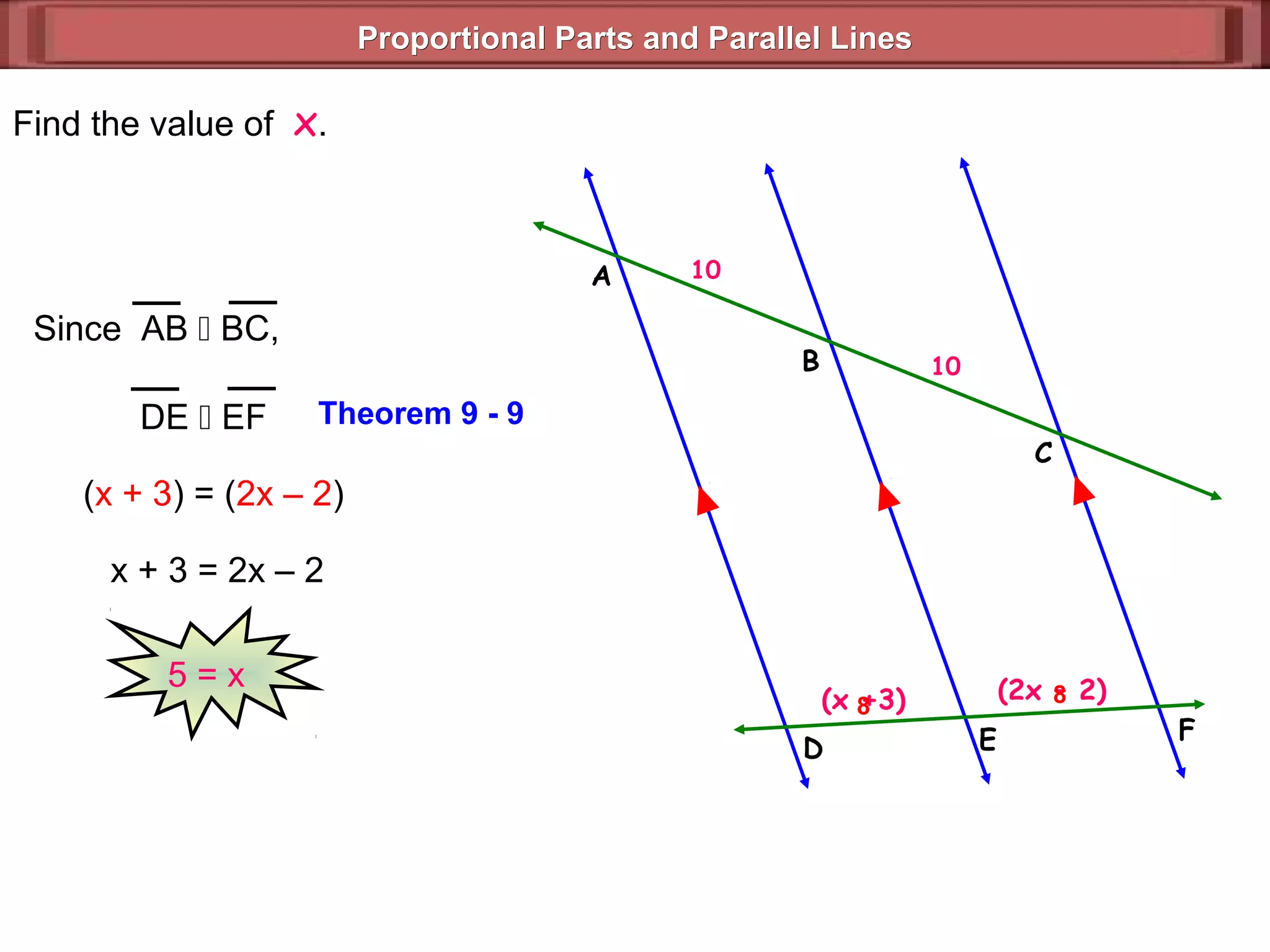
The document discusses proportional parts and parallel lines. It defines that if three or more parallel lines intersect two transversals, the lines divide the transversals proportionally. This means that the ratios of the parts of the first transversal will equal the ratios of the parts of the second transversal. It also states that if three or more parallel lines cut off congruent segments on one transversal, then they cut off congruent segments on every transversal. Examples are provided to demonstrate finding missing values using proportional reasoning with parallel lines.

1. Proportional Parts and Parallel LinesProportional Parts and Parallel Lines
You will learn to identify and use the relationships between
parallel lines and proportional parts.
Nothing New!

2. Proportional Parts and Parallel LinesProportional Parts and Parallel Lines
On your given paper,
draw two (transversals)
lines intersecting the parallel lines.
C
D
E
F
A
BLabel the intersections of the
transversals and the parallel lines,
as shown here.
Measure AB, BC, DE, and EF.
,Calculate each set of ratios:
BC
AB
EF
DE
AC
AB
DF
DE,
Do the parallel lines divide the transversals proportionally? Yes

3. Proportional Parts and Parallel LinesProportional Parts and Parallel Lines
Theorem 9-8
If three or more parallel lines intersect two transversals,
the lines divide the transversals proportionally.
l
m
n
B
A
C F
E
D
If l || m || n
AC
BC
DF
EF
=Then
BC
AB
EF
DE
= ,
AC
AB
DF
DE
= and,

4. Proportional Parts and Parallel LinesProportional Parts and Parallel Lines
a
b
c
H
G
J W
V
U
18
12
x
15
Find the value of x.
HJ
GH
VW
UV
=
18
12
x
15
=
12x = 18(15)
12x = 270
x = 22
2
1

5. Proportional Parts and Parallel LinesProportional Parts and Parallel Lines
Theorem 9-9
If three or more parallel lines cut off congruent segments on
one transversal, then they cut off congruent segments on
every transversal.
l
m
n
B
A
C F
E
D
If l || m || n and
Then
AB  BC,
DE  EF.

6. Proportional Parts and Parallel LinesProportional Parts and Parallel Lines
(x +3)
10
(2x – 2)
10
Find the value of x.
F
(x + 3) = (2x – 2)
x + 3 = 2x – 2
5 = x
Theorem 9 - 9
8 8
ED
C
B
A
DE  EF
Since AB  BC,

7. Proportional Parts and Parallel LinesProportional Parts and Parallel Lines