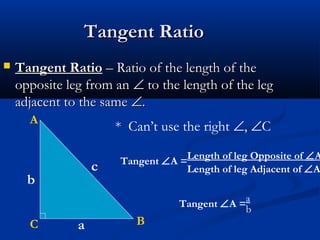
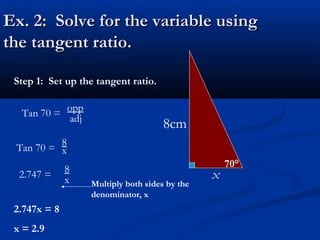
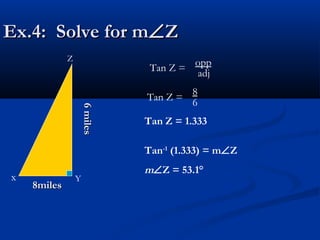
This document discusses using tangent ratios to determine side lengths in right triangles. It defines tangent ratios as the ratio of the length of the opposite leg to the length of the adjacent leg. Tangent ratios can be used to find the measure of distances that are difficult to measure directly. The tangent inverse function, denoted Tan-1, can be used to find a missing angle measure when two sides of a triangle are known. Examples demonstrate setting up and solving tangent ratios and using the tangent inverse to find missing angle measures.

1. Sec. 8 – 3Sec. 8 – 3
The Tangent RatioThe Tangent Ratio
Objective:Objective:
1) To use tangent ratios to1) To use tangent ratios to
determine side lengths indetermine side lengths in ΔΔ..

2. This only for rightThis only for right ΔΔs!!s!!
 TrigonometryTrigonometry
 Greek WordGreek Word
 Trigon → TriangleTrigon → Triangle
 Metron → MeasureMetron → Measure
 Trigonometry RatioTrigonometry Ratio – Ratio of the lengths of– Ratio of the lengths of
sides of a rightsides of a right ΔΔ..

3.  The tangent is just a button on your calculator!The tangent is just a button on your calculator!
TanTan
** Make sure you calculator is in Degrees!!

4. Tangent RatioTangent Ratio
 Tangent RatioTangent Ratio – Ratio of the length of the– Ratio of the length of the
opposite leg from anopposite leg from an ∠∠ to the length of the legto the length of the leg
adjacent to the sameadjacent to the same ∠∠..
A
C B
b
a
c
* Can’t use the right ∠, ∠C
Tangent ∠A =
Length of leg Opposite of ∠A
Length of leg Adjacent of ∠A
Tangent ∠A =
a
b

5. Writing tangent ratiosWriting tangent ratios
 Write the tangent ratio ofWrite the tangent ratio of ∠∠T andT and ∠∠U.U.
T
U
S
6
8
10 Tangent ∠θ =
Opposite
Adjacent
Tangent ∠T =
8
6
TS
US =
Tangent ∠U =TS
US 6
8=
** Tangent ratio for ∠T & ∠U are reciprocals

6. You can use the tangent ratio to findYou can use the tangent ratio to find
the measure of a distance that isthe measure of a distance that is
difficult to measure directly.difficult to measure directly.
 Example 1: Find w.Example 1: Find w.
10
w
54
Step 1: Set up the Tangent Ratio
Tan 54 =
opp
adj
Tan 54 =
w
10
1.376 =
w
10
13.76 = w

7. Ex. 2: Solve for the variable usingEx. 2: Solve for the variable using
the tangent ratio.the tangent ratio.
70°
8cm
x
Step 1: Set up the tangent ratio.
Tan 70 =
opp
adj
Tan 70 =
8
x
2.747 =
8
x Multiply both sides by the
denominator, x
2.747x = 8
x = 2.9

8. The Tangent Inverse: TanThe Tangent Inverse: Tan-1-1
 Just another button on your Calculator!Just another button on your Calculator!
 Use it when you have the two sides of aUse it when you have the two sides of a ΔΔ andand
are trying to find a missingare trying to find a missing ∠∠..
TanTan
Tan-1Use the SHIFT (2nd
)
Key to get to it.
Once you press it, it should
look like this: Tan-1
(

9. Ex.3: Using the TanEx.3: Using the Tan-1-1
 Use the TanUse the Tan-1-1
to solve for the missingto solve for the missing ∠∠..
12mm
5mm
y°
Step 1: Set up the
Tan Ratio
Tan y =
opp
adj
Tan y =
5
12
Tan y = .4167
At this point you will use the Tan-1
:
1) Hit shift Tan to get to
Tan-1
(
2) Type in the decimal and hit enter
Tan-1
(.4167) = 22.6°

10. Ex.4: Solve for mEx.4: Solve for m∠∠ZZ
8miles8miles
6miles6miles
x Y
Z
Tan Z =
opp
adj
Tan Z =
8
6
Tan Z = 1.333
Tan-1
(1.333) = m∠Z
m∠Z = 53.1°

11. What have I learned???What have I learned???
 TanTan θθ ==
 Use TanUse Tan-1-1
when looking for anwhen looking for an ∠∠ measure.measure.
Opposite Side
Adjacent Side