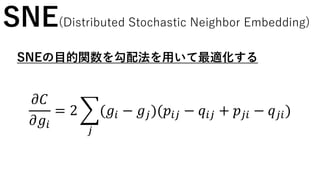More Related Content
PDF
PDF
PDF
Visualizing Data Using t-SNE PDF
12. Diffusion Model の数学的基礎.pdf PDF
#みどりぼん 11章「空間構造のある階層ベイズモデル」後半 PDF
統計的学習理論チュートリアル: 基礎から応用まで (Ibis2012) PDF
PDF
(DL hacks輪読) Variational Dropout and the Local Reparameterization Trick What's hot
PDF
PPTX
PPTX
【LT資料】 Neural Network 素人なんだけど何とかご機嫌取りをしたい PDF
機械学習による統計的実験計画(ベイズ最適化を中心に) PDF
クラシックな機械学習入門:付録:よく使う線形代数の公式 PDF
[DL輪読会]AdaShare: Learning What To Share For Efficient Deep Multi-Task Learning PDF
PDF
Neural networks for Graph Data NeurIPS2018読み会@PFN PDF
PPTX
PDF
PPTX
PDF
PDF
PDF
[DL輪読会]Wasserstein GAN/Towards Principled Methods for Training Generative Adv... PDF
PDF
PPTX
PDF
探索と活用の戦略 ベイズ最適化と多腕バンディット PDF
Similar to T-sne
PPTX
PDF
PPTX
PPTX
PDF
PRML輪講用資料10章(パターン認識と機械学習,近似推論法) PPTX
PDF
A Brief Survey of Schrödinger Bridge (Part I) PDF
PPTX
StanとRでベイズ統計モデリングに関する読書会(Osaka.stan) 第四章 PPT
PDF
PPTX
PDF
PDF
PDF
Learning Latent Space Energy Based Prior Modelの解説 PDF
PDF
StanとRでベイズ統計モデリング読書会 導入編(1章~3章) PPT
PDF
PDF
統計学における相関分析と仮説検定の基本的な考え方とその実践 More from takutori
PDF
slackの会話ネットワークの分析、及びチャネル内活性化指標の提案 PPTX
PDF
Deep learning _linear_algebra___probablity___information PPTX
PPTX
PPTX
PPTX
PPTX
PPTX
T-sne
- 1.
- 2.
- 3.
- 4.
- 5.
- 6.
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17.
- 18.
- 19.
- 20.
- 21.
- 22.
- 23.
- 24.
- 25.
- 26.
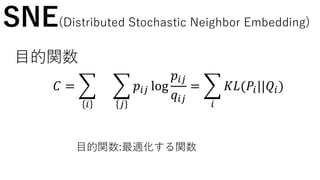
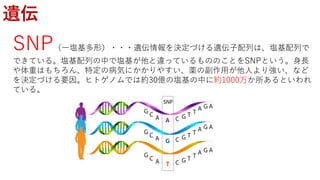
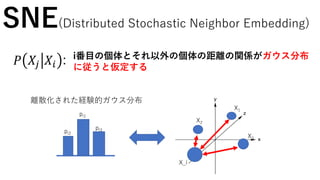
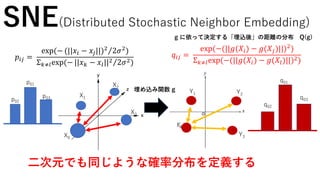
SNE(Distributed Stochastic NeighborEmbedding)
個人1
個人2
個人3
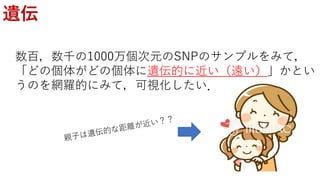
遠い!!
近い!
普通。
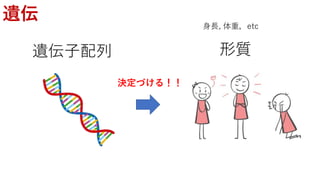
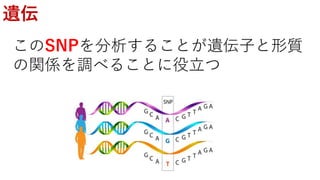
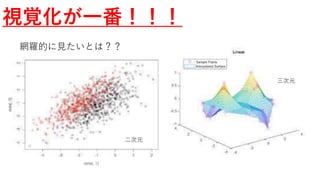
遺伝的距離の関係を保ちながら,高次元のデータを二次元のデータ
に変換することで可視化を可能にしたい
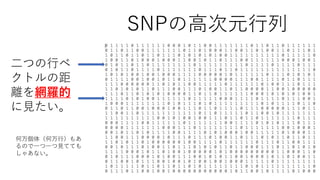
N次元
二次元だと距離関係が
直感的につかめる
個人1 個人2
遠いやつは遠くに!!
近いやつは近くに!
普通は適度に。
個人3
Nが大きいと可視化は難しい
- 27.
- 28.
- 29.
- 30.
- 31.
- 32.
- 33.
𝑞𝑖𝑗 =
exp(−(||𝑔(𝑋𝑖) −𝑔(𝑋𝑗)||)2
)
Σ 𝑘≠𝑙exp(−(||𝑔(𝑋𝑖) − 𝑔(𝑋𝑙)||)2)
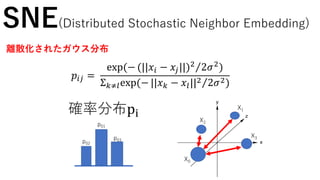
𝑝𝑖𝑗 =
exp(− (||𝑥𝑖 − 𝑥𝑗||)2
2𝜎2
)
Σ 𝑘≠𝑙exp(− ||𝑥 𝑘 − 𝑥𝑙||2 2𝜎2)
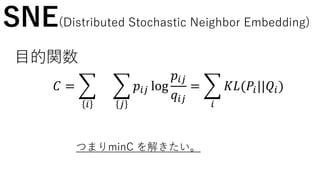
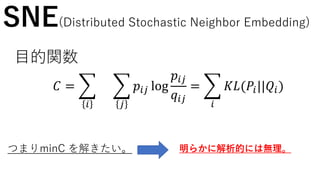
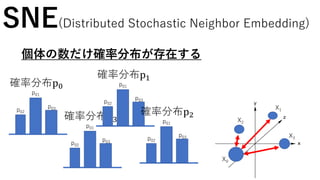
SNE(Distributed Stochastic Neighbor Embedding)
この二つの分布をなるべく同じような分布になる
ようにしたい!!
高次元の距離の情報を持った確率
分布p
低次元の距離の情報を持った確率
分布p
- 34.
𝑞𝑖𝑗 =
exp(−(||𝑔(𝑋𝑖) −𝑔(𝑋𝑗)||)2
)
Σ 𝑘≠𝑙exp(−(||𝑔(𝑋𝑖) − 𝑔(𝑋𝑙)||)2)
𝑝𝑖𝑗 =
exp(− (||𝑥𝑖 − 𝑥𝑗||)2
2𝜎2
)
Σ 𝑘≠𝑙exp(− ||𝑥 𝑘 − 𝑥𝑙||2 2𝜎2)
SNE(Distributed Stochastic Neighbor Embedding)
分布間の違いを図る物差しはないのか??
高次元の距離の情報を持った確率
分布p
低次元の距離の情報を持った確率
分布p
p01
p02
p03
q01
q02
q03
- 35.
𝑞𝑖𝑗 =
exp(−(||𝑔(𝑋𝑖) −𝑔(𝑋𝑗)||)2
)
Σ 𝑘≠𝑙exp(−(||𝑔(𝑋𝑖) − 𝑔(𝑋𝑙)||)2)
𝑝𝑖𝑗 =
exp(− (||𝑥𝑖 − 𝑥𝑗||)2
2𝜎2
)
Σ 𝑘≠𝑙exp(− ||𝑥 𝑘 − 𝑥𝑙||2 2𝜎2)
SNE(Distributed Stochastic Neighbor Embedding)
分布間の違いを図る物差しはないのか??
高次元の距離の情報を持った確率
分布p
低次元の距離の情報を持った確率
分布p
KLダイバージェンス
- 36.
- 37.
- 38.
- 39.
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46.
- 47.
- 48.
- 49.
- 50.
- 51.
- 52.
- 53.
- 54.
- 55.
自己エントロピー
𝐼 𝑃1 𝑃2= 𝐼 𝑃1 + 𝐼 𝑃2
𝑃1 ≤ 𝑃2ならば𝐼 𝑃1 ≥ 𝐼(𝑃2)
このような性質を満たす関数Iって???
答えは−𝐥𝐨𝐠‼
- 56.
- 57.
- 58.
- 59.
- 60.
- 61.
- 62.
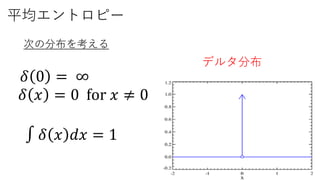
平均エントロピー
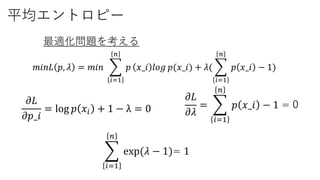
min𝐿 𝑝, 𝜆= 𝑚𝑖𝑛 𝑖=1
𝑛
𝑝 𝑥_𝑖 𝑙𝑜𝑔 𝑝(𝑥_𝑖) + 𝜆( 𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1)
最適化問題を考える
𝜕𝐿
𝜕𝜆
=
𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1 = 0
𝜕𝐿
𝜕𝑝_𝑖
= log 𝑝 𝑥𝑖 + 1 − λ = 0
- 63.
平均エントロピー
min𝐿 𝑝, 𝜆= 𝑚𝑖𝑛 𝑖=1
𝑛
𝑝 𝑥_𝑖 𝑙𝑜𝑔 𝑝(𝑥_𝑖) + 𝜆( 𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1)
最適化問題を考える
𝜕𝐿
𝜕𝜆
=
𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1 = 0𝜕𝐿
𝜕𝑝_𝑖
= log 𝑝 𝑥𝑖 + 1 − λ = 0
𝑝 𝑥𝑖 = exp(𝜆 − 1)
𝑖=1
𝑛
𝑝 𝑥_𝑖 = 1
- 64.
平均エントロピー
min𝐿 𝑝, 𝜆= 𝑚𝑖𝑛 𝑖=1
𝑛
𝑝 𝑥_𝑖 𝑙𝑜𝑔 𝑝(𝑥_𝑖) + 𝜆( 𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1)
最適化問題を考える
𝜕𝐿
𝜕𝜆
=
𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1 = 0𝜕𝐿
𝜕𝑝_𝑖
= log 𝑝 𝑥𝑖 + 1 − λ = 0
𝑝 𝑥𝑖 = exp(𝜆 − 1)
𝑖=1
𝑛
𝑝 𝑥_𝑖 = 1
代入
- 65.
平均エントロピー
𝑚𝑖𝑛𝐿 𝑝, 𝜆= 𝑚𝑖𝑛
𝑖=1
𝑛
𝑝 𝑥_𝑖 𝑙𝑜𝑔 𝑝(𝑥_𝑖) + 𝜆(
𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1)
最適化問題を考える
𝜕𝐿
𝜕𝜆
=
𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1 = 0𝜕𝐿
𝜕𝑝_𝑖
= log 𝑝 𝑥𝑖 + 1 − λ = 0
𝑖=1
𝑛
exp(𝜆 − 1)= 1
- 66.
平均エントロピー
min𝐿 𝑝, 𝜆= 𝑚𝑖𝑛 𝑖=1
𝑛
𝑝 𝑥_𝑖 𝑙𝑜𝑔 𝑝(𝑥_𝑖) + 𝜆( 𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1)
最適化問題を考える
𝜕𝐿
𝜕𝜆
=
𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1 = 0𝜕𝐿
𝜕𝑝_𝑖
= log 𝑝 𝑥𝑖 + 1 − λ = 0
𝑖=1
𝑛
exp(𝜆 − 1)= 1 n exp(𝜆 − 1)=1 n exp(𝜆 − 1)=1
- 67.
平均エントロピー
min𝐿 𝑝, 𝜆= 𝑚𝑖𝑛 𝑖=1
𝑛
𝑝 𝑥_𝑖 𝑙𝑜𝑔 𝑝(𝑥_𝑖) + 𝜆( 𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1)
最適化問題を考える
𝜕𝐿
𝜕𝜆
=
𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1 = 0𝜕𝐿
𝜕𝑝_𝑖
= log 𝑝 𝑥𝑖 + 1 − λ = 0
n exp(𝜆 − 1)=1 P(x_i) =1/n
𝑝 𝑥𝑖 = exp 𝜆 − 1 に代入
𝜆 − 1=log(1/n)
- 68.
平均エントロピー
minL 𝑝, 𝜆= 𝑚𝑖𝑛 𝑖=1
𝑛
𝑝 𝑥_𝑖 𝑙𝑜𝑔 𝑝(𝑥_𝑖) + 𝜆( 𝑖=1
𝑛
𝑝 𝑥_𝑖 − 1)
最適化問題を考える
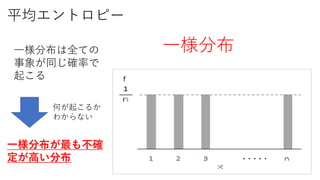
𝑃 𝑥𝑖 =
1
𝑛
の解は
一様分布
- 69.
- 70.
- 71.
- 72.
- 73.
- 74.
- 75.
- 76.
- 77.
- 78.
- 79.
- 80.
𝑞𝑖𝑗 =
exp(−(||𝑔(𝑋𝑖) −𝑔(𝑋𝑗)||)2
)
Σ 𝑘≠𝑙exp(−(||𝑔(𝑋𝑖) − 𝑔(𝑋𝑙)||)2)𝑝𝑖𝑗 =
exp(− (||𝑥𝑖 − 𝑥𝑗||)2
2𝜎2
)
Σ 𝑘≠𝑙exp(− ||𝑥 𝑘 − 𝑥𝑙||2 2𝜎2)
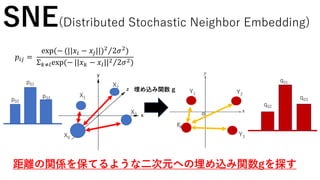
SNE(Distributed Stochastic Neighbor Embedding)
高次元の距離の情報を持った確率
分布p
低次元の距離の情報を持った確率
分布p
この二つの分布をできるだけ近づけるような関数gを知りたい。
KLダイバージェンスを使って目的関数を
作り、gについて最適化をする。
- 81.
- 82.
- 83.
- 84.
- 85.
- 86.
- 87.
SNE(Distributed Stochastic NeighborEmbedding)
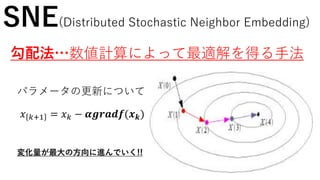
SNEの目的関数を勾配法を用いて最適化する
𝑔
𝑘+1
= 𝑔 𝑘 − 𝛼
2
𝑗
(𝑔1 − 𝑔𝑗)(𝑝1𝑗 − 𝑞1𝑗 + 𝑝𝑗1 − 𝑞 𝑗1)
2
𝑗
(𝑔2 − 𝑔𝑗)(𝑝2𝑗 − 𝑞2𝑗 + 𝑝𝑗2 − 𝑞 𝑗2)
⋮
⋮
2
𝑗
(𝑔 𝑛 − 𝑔𝑗)(𝑝 𝑛𝑗 − 𝑞 𝑛𝑗 + 𝑝𝑗𝑛 − 𝑞 𝑗𝑛)
- 88.
- 89.
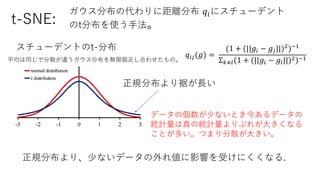
ガウス分布の代わりに距離分布 𝑞𝑖にスチューデント
のt分布を使う手法。
𝑞𝑖𝑗(𝑔) =
(1+ (||𝑔𝑖 − 𝑔𝑗||)2
)−1
Σ 𝑘≠𝑙(1 + (||𝑔𝑖 − 𝑔𝑙||)2)−1
データの個数が少ないとき今あるデータの
統計量は真の統計量よりぶれが大きくなる
ことが多い。つまり分散が大きい。
t-SNE:
スチューデントのt-分布
平均は同じで分散が違うガウス分布を無限個足し合わせたもの。
正規分布より裾が長い
正規分布より、少ないデータの外れ値に影響を受けにくくなる。
- 90.
- 91.
- 92.
- 93.
- 94.
- 95.
Editor's Notes
- #90 青の分布は裾のほうの極端な値もあり得ると考えている。
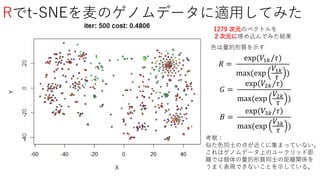
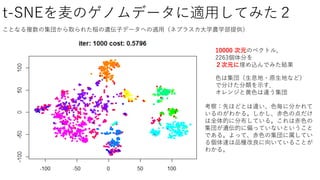
- #92 tau で色の濃さの極端度をコントロール 0で最極端、結論:二つの個体の間に存在する量的形質の差がゲノム空間上の距離に反映されるように距離を設定しなければいけない。




































![平均エントロピー
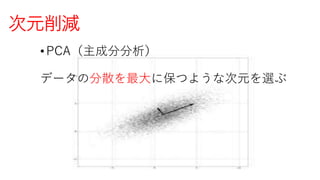
定義
確率分布Pの平均エントロピーは
𝐸[− log 𝑃 𝐸 ]](https://image.slidesharecdn.com/t-snesuuken-180921110102/85/T-sne-58-320.jpg)
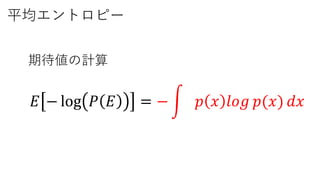














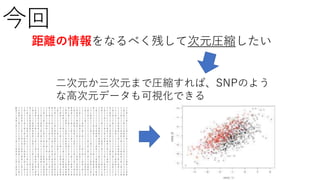
![KLダイバージェンス
PとQでは情報量はどれくらい違うだろうか???
− log 𝑄 − − log 𝑃 = log
𝑃
𝑄
の期待値をとると
𝑬[𝐥𝐨𝐠
𝑷(𝒙)
𝑸(𝒙)
] =
−∞
∞
𝑷(𝒙)
𝐥𝐨𝐠 𝑷 𝒙
𝑸 𝒙
𝒅𝒙](https://image.slidesharecdn.com/t-snesuuken-180921110102/85/T-sne-77-320.jpg)
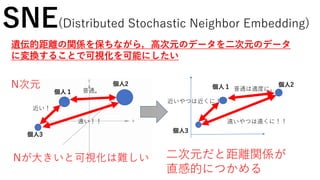
![KLダイバージェンス
𝑬[𝐥𝐨𝐠
𝑷(𝒙)
𝑸(𝒙)
] =
−∞
∞
𝑷 𝒙
𝐥𝐨𝐠 𝑷 𝒙
𝑸 𝒙
𝒅𝒙 =: 𝑲𝑳(𝑷||𝑸)
分布間の違いを図る尺度として使われる。
KLダイバージェンス](https://image.slidesharecdn.com/t-snesuuken-180921110102/85/T-sne-78-320.jpg)