تتحدث الوثيقة عن نظريات الهندسة الأساسية، حيث تشمل قوانين قياس الزوايا في المثلثات والمضلعات وأنواع الأشكال الهندسية مثل المستطيل والمربع. كما تتناول أدوات التحويل الهندسي والعلاقات بين الزوايا القياسية وأبعاد الأشكال. أخيراً، تشمل المعادلات الرياضية المرتبطة بتطبيقات هذه النظريات.

1. ‫أول‬:‫ملخص‬‫نظريات‬‫الهندسة‬
1-‫إذا‬‫تقاطع‬‫مستقيمان‬‫فإن‬‫كل‬‫زاويتان‬‫متقابلتان‬‫بالرأس‬‫تكونان‬
‫متساويتان‬‫في‬‫القياس‬
2-‫مجموع‬‫قياسات‬‫الزوايا‬‫المتجمعة‬‫حول‬‫نقطة‬‫تساوي‬360ْ
3-‫مجموع‬‫قياسات‬‫الزوايا‬‫الداخلة‬‫للمثلث‬‫تساوي‬180ْ
4-‫قياس‬‫أي‬‫زاوية‬‫خارجة‬‫عن‬‫المثلث‬‫تساوي‬‫مجموع‬‫قياسي‬
‫الزاويتان‬‫الداخلتان‬‫عدا‬‫المجاورة‬‫لها‬
5-‫مجموع‬‫الزوايا‬‫الداخلة‬‫لي‬‫مضلع‬‫ن‬ ) =–2(×180
6-‫مجموع‬‫قياسات‬‫الزوايا‬‫الداخلة‬‫للشكل‬‫الرباعي‬=360ْ
7-‫مجموع‬‫الزوايا‬‫الداخلة‬‫للخماسي‬=540ْ،‫السداسي‬=720ْ
8-‫المضلع‬‫المنتظم‬‫هو‬‫المضلع‬‫الذي‬‫جميع‬‫أضلعه‬‫متساوية‬‫في‬
‫الطول‬‫و‬‫جميع‬‫زواياه‬‫متساوية‬‫في‬‫القياس‬
9-‫قياس‬‫الزاوية‬‫الداخلة‬‫للمضلع‬‫المنتظم‬=‫ن‬ )–2(×180
‫ن‬
‫قياس‬‫زاوية‬‫المثلث‬‫المتساوي‬‫الضلع‬=‫الداخلة‬605
‫والخارجة‬120
10-‫مجموع‬‫الزوايا‬‫الخارجة‬‫لي‬‫مضلع‬=360،ْ
11-‫القطعة‬‫المستقيمة‬‫المرسومة‬‫بين‬‫منتصفي‬‫ضلعين‬‫في‬‫مثلث‬
‫توازى‬‫الضلع‬‫الثالث‬‫وتساوي‬‫نصف‬‫طوله‬.
12-‫الشعاع‬‫المرسوم‬‫من‬‫منتصف‬‫ضلع‬‫من‬‫مثلث‬‫موازيا‬‫أحد‬
‫الضلعين‬‫الخرين‬‫ينصف‬‫الضلع‬‫الثالث‬
13-‫إذا‬‫ساوى‬‫قياس‬‫زاوية‬‫في‬‫مثلث‬‫مجموع‬‫الزاويتان‬‫الخرتان‬‫كان‬
‫المثلث‬‫قائم‬‫الزاوية‬.
14-‫إذا‬‫ساوى‬‫زاويتان‬‫في‬‫مثلث‬‫زاويتان‬‫في‬‫مثلث‬‫أخر‬‫فإن‬‫قياس‬
‫الزاويةالثالثة‬‫في‬‫المثلث‬‫الول‬‫=قياس‬‫الزاوية‬‫الثالثة‬‫في‬‫المثلث‬‫الخر‬
15‫الشكل‬ -‫الرباعي‬‫الذي‬‫فيه‬‫ضلعان‬‫فقط‬‫متوازيان‬‫يسمى‬‫شبه‬‫منحرف‬
16‫متوازي‬ -‫الضلع‬‫الذي‬‫إحدى‬‫زواياه‬‫قائمة‬‫يكون‬)(‫مستطيل‬
17‫المعين‬ -‫الذي‬‫إحدى‬‫زواياه‬‫قائمة‬‫يكون‬‫مربـع‬ )(
18‫متوازي‬ -‫الضلع‬‫الذي‬‫قطراه‬‫متساويان‬)‫يكون‬‫مستطيل‬(،

2. ‫قطراه‬‫متعامدان‬‫يكون‬، (‫)معين‬‫متساويان‬‫ومتعامدان‬‫يكون‬(‫)مربع‬
19‫والمربع‬ ‫والمعين‬ ‫والمستطيل‬ ‫اللضل ع‬ ‫متوازي‬ ‫خواص‬ ‫ملخص‬ -
‫الشكل‬‫اللضل ع‬‫الزوايا‬‫القطران‬
‫متوازي‬
‫اللضل ع‬
‫متقابلن‬ ‫لضلعان‬ ‫كل‬
‫متوازيان‬
‫في‬ ‫ومتساويان‬
‫الطول‬
‫المتقابلتان‬
‫متساويتان‬
‫والمتتاليتان‬
‫متكاملتان‬
‫كل‬ ‫ينصف‬ ‫القطران‬
‫الخر‬ ‫منهما‬
‫المستطيل‬‫اللضل ع‬ ‫متوازي‬ ‫نفس‬‫قـوائـم‬ ‫زوايـاه‬‫متساويان‬ ‫قطراه‬
‫المعين‬
‫متساوية‬ ‫ألضلهعه‬
‫الطول‬ ‫في‬
‫متوازي‬ ‫نفس‬
‫اللضل ع‬
‫متعامدان‬ ‫القطران‬
‫زواياه‬ ‫ينصفان‬ ‫و‬
‫المربع‬
‫متساوية‬ ‫ألضلهعه‬
‫الطول‬ ‫في‬
‫قـوائـم‬ ‫زوايـاه‬‫سبق‬ ‫ما‬ ‫جميع‬
20‫نظرية‬ -‫فيثاغورث‬‫في‬ ) :‫المثلث‬‫القائم‬‫الزاوية‬‫مربع‬ :‫طول‬
‫الوتر‬‫مجموع‬ =‫مربعي‬‫طولي‬‫ضلعي‬‫القائمة‬‫أ‬
21‫ليجاد‬ -‫الوتر‬‫نجمع‬‫لنه‬‫أكبر‬‫ضلع‬‫أي‬ :‫أن‬
‫)أ‬‫جـ‬(2
‫=)أ‬(‫ب‬2
‫)ب‬ +(‫جـ‬2
‫جـ‬‫ب‬
22‫نطرح‬ ‫القائمة‬ ‫لضلعي‬ ‫أحد‬ ‫-ليجاد‬( ‫جـ‬ ‫)ب‬2
( ‫جـ‬ ‫)أ‬ =2
(‫ب‬ ‫)أ‬ –2
) ‫القائمة‬ ‫المثلثات‬ ‫بعض‬3،4،5) (6،8،10) (5،12،13(
23: ‫الهندسية‬ ‫التحويلت‬ ‫ملخص‬ -
‫النقطة‬‫التحويلة‬‫الهندسية‬‫صورة‬‫النقطة‬
‫س‬ )(‫ص‬ ,
‫بالنعكاس‬‫في‬‫محور‬‫السينات‬‫س‬ )‫ص‬ - ,(
‫بالنعكاس‬‫في‬‫محور‬‫الصادات‬‫س‬ - )‫ص‬ ,(
‫بالنعكاس‬‫في‬‫نقطة‬‫الصل‬‫س‬ - )‫ص‬ - ,
‫بالنتقال‬‫جـ‬ )‫د‬ ,(‫)نجمع‬ (‫ص‬ ,‫جـ‬ +‫س‬ )(‫د‬ +
‫بالدوران‬‫بزاوية‬180- ,180‫س‬ - )(‫ص‬ - ,
‫بالدوران‬‫بزاوية‬‫)و‬،90(‫ص‬ - )‫س‬ ,(
‫بالدوران‬‫و‬ )‫بزاوية‬،–90(‫ص‬ )(‫س‬ - ,
24= ‫المربع‬ ‫تماثل‬ ‫محاور‬ ‫هعدد‬ -4= ‫اللضل ع‬ ‫المتساوي‬ ‫المثلث‬ ،
3= ‫المعين‬ ‫أو‬ ‫المستطيل‬ ،2‫لنهائي‬ ‫هعدد‬ = ‫الدائرة‬

3. = ‫الساقين‬ ‫متساوي‬ ‫المنحرف‬ ‫شبه‬ ‫أو‬ ‫الساقين‬ ‫المتساوي‬ ‫المثلث‬1
‫=صفر‬ ‫اللضل ع‬ ‫متوازي‬ ‫أو‬ ‫اللضل ع‬ ‫المختلف‬ ‫المثلث‬ ،
‫السالبة‬ ‫غير‬ ‫الصحيحة‬ ‫القوى‬
‫س‬1: ‫مايأتي‬ ‫أكمل‬ :
1(22
،..... =23
، .... =24
، .... =25
......=
2(32
، .....=33
، .... =34
، ..... =35
......=
3(52
،....=53
، .... =54
، ..... =5‫صفر‬
.....=
4(-)3(‫صفر‬
) ، ......... =3(3
...... =
52
5) (12(2
- ) ..………=21(2
...... =
43
6) ‫للعدد‬ ‫الجمعي‬ ‫المعكوس‬ (3(‫صفر‬
.............. ‫هو‬
7-) ‫للعدد‬ ‫الجمعي‬ ‫المعكوس‬ (1(6
.............. ‫هو‬
8-) ‫للعدد‬ ‫الضربي‬ ‫المعكوس‬ (5(‫صفر‬
......... ‫هو‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2‫صورة‬ ‫لبسط‬ ‫اختصر‬ :35
×37
3×38
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3‫صورة‬ ‫لبسط‬ ‫اختصر‬ :27
×39
25
×38
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬4= ‫س‬ ‫كان‬ ‫إذا‬ (‫)أ‬ :3- = ‫ص‬ ،4= ‫ ع‬ ،5‫أوجد‬
‫س‬ ‫للمقدار‬ ‫العددية‬ ‫القيمة‬2
‫ص‬ +2
‫هع‬ ×‫صفر‬

4. = ‫أ‬ ‫كان‬ ‫إذا‬ (‫)ب‬4= ‫ب‬ ،1- = ‫جـ‬ ،4‫ب‬ - ‫أ‬ : ‫قيمة‬ ‫أوجد‬2
‫جـ‬
525
2‫السالبة‬ ‫الصحيحة‬ ‫القوى‬ -
‫س‬1: ‫مايأتي‬ ‫أكمل‬ :
1(2-2
،.............. =2-3
، ............. =2-1
.......=
2(3‫س‬
=5‫فإن‬3+ ‫س‬1
.............. =
3) (3(-2
) ، .................. =2(-3
............... =
53
4-) (5(-2
) ..........=-3(-3
..........=
4
5(7‫س‬-3
) ، .............. =3( ‫س‬-1
.............=
6‫س‬ (2
‫س‬ ×3
‫س‬ ، ............. =7
‫س‬ ÷3
........ =
7‫س‬ ) (2
(3
‫س‬ ) ........=2
‫ص‬3
(5
........=
8(39
+39
+39
=، ...........27
+27
......... =
9‫العدد‬ ‫نصف‬ (28
‫العدد‬ ‫ربع‬ ، ....... =420
........... =
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2‫صورة‬ ‫لسبسط‬ ‫اختصر‬ :2-3
×27
-)2(4
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3‫صورة‬ ‫لسبسط‬ ‫اختصر‬ :‫س‬-5
‫س‬ ×11
‫س‬ )2
(3
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬4= ‫س‬ ‫كان‬ ‫إذا‬ :3= ‫ص‬ ،-4= ‫ع‬ ،5
293

5. ‫س‬ ‫للمقدار‬ ‫العددية‬ ‫القيمة‬ ‫أوجد‬2
‫ع‬ ÷ ‫ص‬-2
3-‫النسبي‬ ‫للعدد‬ ‫التربيعي‬ ‫الجذر‬
‫س‬1: ‫مايأتي‬ ‫أكمل‬ :
1(‫للعدد‬ ‫التربيعي‬ ‫الجذر‬25......... ‫هو‬
2(36- ، ....... =36± ، ......... =36... =
3(81، ........... =16.......... =
4(25، ........... =0.25........ =
49
5(12..………=16...... =
44
6‫س‬ (2
‫ص‬4
‫ ع‬6
............=25‫م‬2
...........=
7(9+16- ) ........... =3(2
.......=
8(36+64=6– ...... +9........ =
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2- ‫اختصر‬ (‫أ‬ ) :32
×25- ×2‫صفر‬
5817
(‫ص‬ ‫)س‬ ‫حيث‬ ‫مستقيمة‬ ‫قطعة‬ ‫ص‬ ‫س‬ (‫)ب‬2
=36
‫ ع‬ ‫س‬ ‫طول‬ ‫أوجد‬ ‫ص‬ ‫س‬ ‫منتصف‬ ‫ ع‬ ،
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3‫قاهعدته‬ ‫طول‬ ‫مثلث‬ ‫مساحة‬ ‫تساوي‬ ‫مساحتة‬ ‫مربع‬ :10‫سم‬
‫وارتفاهعه‬5‫المربع‬ ‫لضلع‬ ‫طول‬ ‫أوجد‬ ‫سم‬

6. 4‫النسبي‬ ‫للعدد‬ ‫القياسية‬ ‫الصورة‬ -
‫س‬1‫القياسية‬ ‫الصورة‬ ‫هعلى‬ ‫التية‬ ‫الهعداد‬ ‫لضع‬ :
1(4560000=......................
2(58= ‫مليون‬..................
3(0,000045=.............
4(0.000456=..................
5(0,007×0,005=...........
6(35×104
...... =
7(0,0037×10-2
=.............
8) ‫الكبر‬ ‫هو‬ ‫يأتي‬ ‫مما‬ ‫أي‬ (6,3×105
،9,8×104
،5,2×105
،7,3×104
(
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2: ‫مايأتي‬ ‫أكمل‬ :
1(0,00073=7,3×10‫ن‬
....= ‫ن‬ ‫فإن‬
2(4500000=4,5×10......
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3‫القياسية‬ ‫الصورة‬ ‫هعلى‬ ‫مايلي‬ ‫ناتج‬ ‫أوجد‬ :
) (‫أ‬ )1,3×104
) × (5×102
(
) (‫)ب‬3,8×108
) ÷ (1,9×106
(
) (‫)جـ‬3,8×105
) + (4,6×104
(

7. 5-‫الحسابيه‬ ‫العمليات‬ ‫ترتيب‬
‫س‬1: ‫مايأتي‬ ‫أكمل‬ :
1‫هي‬ ‫الحسابيه‬ ‫العمليات‬ ‫ترتيب‬ ‫خطوات‬ (
.........,....................... ،............... ، .............
.........
2(3+2×5=........
3(8÷2+3×5=...........
4(32
+23
×5–15÷3=...........
5(7) +4+6÷ (5–23
=...........
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2(‫أ‬ ) ‫قيمة‬ ‫أوجد‬ :3) ]62
+1) - (33
–1[ (
(‫)ب‬3) +5+2)8÷4( (
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3‫قيمة‬ ‫احسب‬ :(‫أ‬ )5+2×5+52
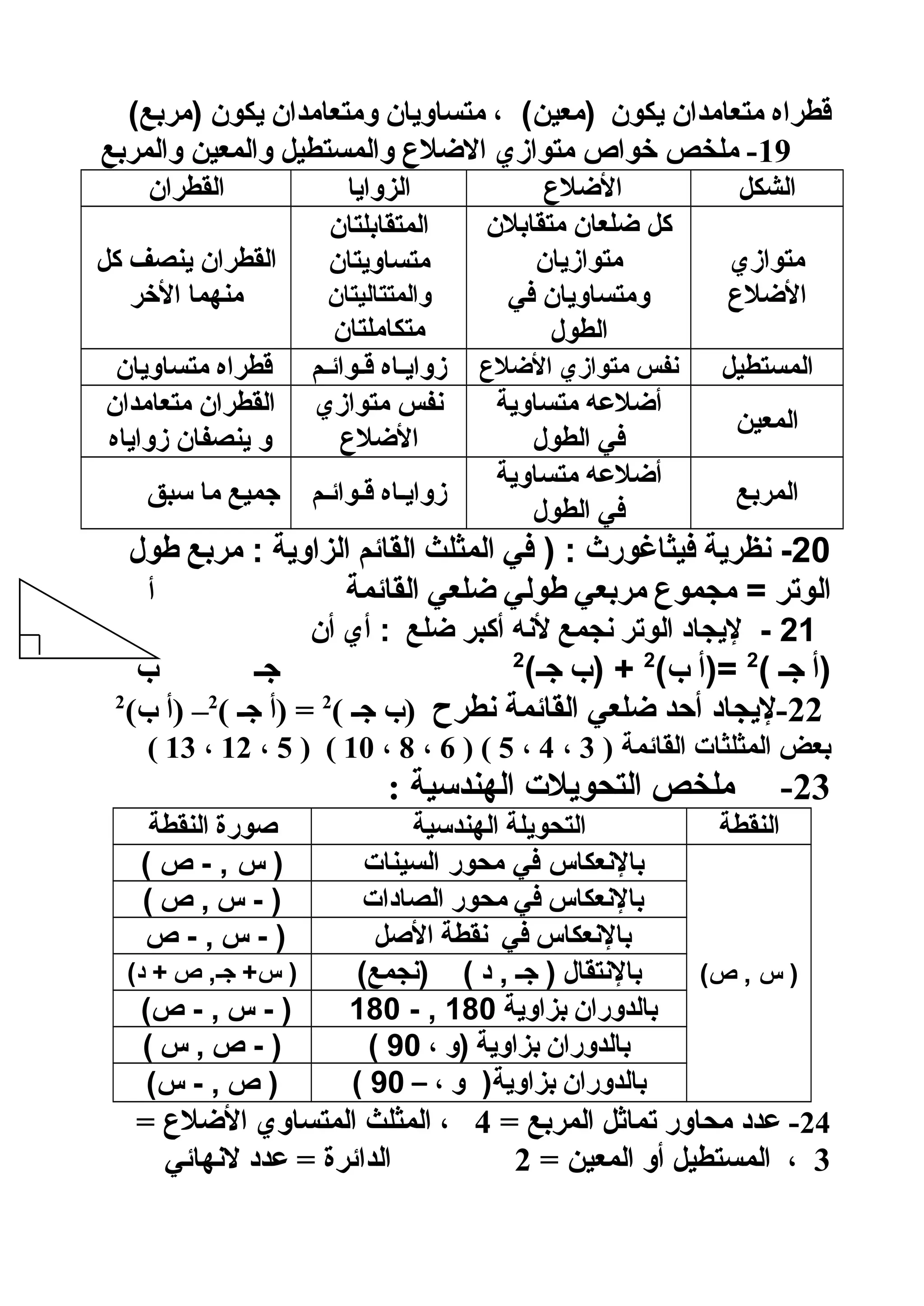
–5
22
+1
(‫)ب‬32
×6÷3
2×1) +3+1(2
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬

8. ‫س‬4= ‫س‬ ‫كان‬ ‫اذا‬ :3‫المقدار‬ ‫قيمة‬ ‫فما‬2)5+ ‫س‬3(
4– ‫س‬3
6‫ن‬ ‫في‬ ‫المعادلت‬ ‫حل‬ -
‫س‬1‫ن‬ ‫في‬ ‫التية‬ ‫المعادلت‬ ‫حل‬ ‫مجموعة‬ ‫أوجد‬ :
(‫)أ‬8+ ‫س‬4=12(‫)ب‬3– ‫س‬13=26
(‫)جـ‬5– ‫س‬4=11(‫)د‬5– ‫س‬4=2+ ‫س‬11
6
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2‫ومجموعهما‬ ‫الخر‬ ‫ضعف‬ ‫أحدهما‬ ‫طبيعيان‬ ‫عددان‬ ( ‫أ‬ ) :
108‫العددان‬ ‫أوجد‬
‫مجموعهم‬ ‫متتالية‬ ‫زوجية‬ ‫أعداد‬ ‫ةثلةثة‬ ‫أوجد‬ (‫)ب‬966

9. 6-‫ن‬ ‫في‬ ‫المتباينات‬ ‫حل‬
‫س‬1‫ن‬ ‫في‬ ‫التية‬ ‫المتباينات‬ ‫حل‬ ‫مجموعة‬ ‫أوجد‬ :
+ ‫س‬ (‫)أ‬4<1(‫)ب‬19+ ‫ص‬ >14
(‫)جـ‬2–3< ‫س‬8(‫)د‬5< ‫س‬ –3
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2‫ن‬ ‫في‬ ‫التية‬ ‫المتباينات‬ ‫حل‬ ‫مجموعة‬ ‫أوجد‬ :
(‫)أ‬5>2+ ‫س‬1>7
(‫)ب‬3>5> ‫س‬ –9

10. 7-‫الحتمال‬
‫س‬1: ‫مايأتي‬ ‫أكمل‬ :
1.......... = ‫والمؤكد‬ ، ............ = ‫المستحيل‬ ‫الحدث‬ ‫احتمال‬ -
2.......... = ‫الصورة‬ ‫ظهور‬ ‫احتمال‬ ‫فإن‬ ‫نقود‬ ‫قطعة‬ ‫القاء‬ ‫عند‬ -
3.............. = ‫عشوائية‬ ‫لتجربة‬ ‫الممكنة‬ ‫الحتمالت‬ ‫مجموع‬ -
4‫هو‬ ‫احمد‬ ‫نجاح‬ ‫احتمال‬ ‫كان‬ ‫اذا‬ -0.7= ‫رسوبه‬ ‫احتمال‬ ‫فان‬
5‫حدث‬ ‫وقوع‬ ‫احتمال‬ -80..... = ‫وقوعه‬ ‫عدم‬ ‫احتمال‬ ‫فان‬ %
7‫فريق‬ ‫فوز‬ ‫احتمال‬ -3............. = ‫فوزه‬ ‫عدم‬ ‫احتمال‬ ،‫فإ‬
5
8‫احتمال‬ ‫فإن‬ ‫واحده‬ ‫مره‬ ‫منتظم‬ ‫نرد‬ ‫حجر‬ ‫القاء‬ ‫تجربة‬ ‫في‬ -
....... = ‫أولي‬ ،......... =‫فردي‬ ، ...........= ‫زوجي‬ ‫عدد‬ ‫ظهور‬
‫على‬ ‫القسمه‬ ‫يقبل‬ ‫عدد‬3................... =
9‫احتمال‬ ‫فان‬ (‫جبر‬ ) ‫كلمة‬ ‫حروف‬ ‫من‬ ‫حرف‬ ‫اختيار‬ ‫عند‬ -
.............. ‫هو‬ ‫ج‬ ‫حرف‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2:‫على‬ ‫يحتوي‬ ‫صندوق‬3، ‫بيضاء‬ ‫كرات‬5، ‫زرقاء‬4
: ‫تكون‬ ‫أن‬ ‫احتمال‬ ‫أوجد‬ ‫عشوائيا‬ ‫كرة‬ ‫سحبت‬ ، ‫حمراء‬
1-‫زرقاء‬
2-‫حمراء‬ ‫ليست‬
3-‫حمراء‬ ‫أو‬ ‫زرقاء‬
4-‫خضراء‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2‫من‬ ‫بطاقة‬ ‫:سحبت‬9‫من‬ ‫مرقمة‬ ‫بطاقة‬1:9‫عدد‬ ‫احتمال‬ ‫أوجد‬

11. 1-‫على‬ ‫القسمة‬ ‫يقبل‬3
2-‫زوجي‬ ‫عدد‬
3-‫يساوي‬ ‫أو‬ ‫من‬ ‫أكبر‬ ‫عدد‬6
‫الهندسة‬ ‫ةثانيا‬1‫الستدللي‬ ‫البرهان‬ -
‫س‬1‫مايأتي‬ ‫أكمل‬ :
1-‫تكونان‬ ‫بالرأس‬ ‫متقابلتان‬ ‫زاويتان‬ ‫كل‬ ‫فإن‬ ‫مستقيمان‬ ‫تقاطع‬ ‫إذا‬.....
2-‫نقطة‬ ‫حول‬ ‫المتجمعة‬ ‫الزوايا‬ ‫قياسات‬ ‫مجموع‬............ =
3-.............. = ‫والقائمة‬ ................ = ‫المستقيمة‬ ‫الزاوية‬ ‫قياس‬
4-........ ، ....... = ‫س‬ ‫قيمة‬ ‫المقابلين‬ ‫الشكلين‬ ‫في‬
4‫س‬
2‫س‬3‫س‬5‫س‬
5‫ب‬ ‫أ‬ ‫المقابل‬ ‫الشكل‬ ‫في‬ -
...... = (‫ب‬ > )‫ق‬ ، ................. = ( ‫أ‬ > )‫ق‬
505
‫جـ‬ ‫د‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2:( ‫د‬ ‫ب‬ ‫هـ‬ > )‫ق‬ ‫أوجد‬ : ‫المقابل‬ ‫الشكل‬ ‫في‬
‫جـ‬
1105
35
‫أ‬‫ب‬
1405
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬‫هـ‬
‫س‬3‫أوجد‬ ‫المقابل‬ ‫الشكل‬ ‫في‬ :
1(‫د‬ ‫جـ‬ ( ‫هـ‬ ‫ب‬ ‫د‬ > ) ‫ق‬
2(( ‫جـ‬ ‫ب‬ ‫د‬ > )‫ق‬‫أ‬305

12. 405
‫هـ‬ ‫ب‬
‫و‬
1-‫المضلع‬
‫س‬1‫مايأتي‬ ‫أكمل‬ :
1-‫اضلعه‬ ‫عدد‬ ‫مضلع‬ ‫لي‬ ‫الداخلة‬ ‫الزوايا‬ ‫قياسات‬ ‫مجموع‬
= ‫ن‬.................
2-‫المضلع‬‫المنتظم‬‫هو‬‫المضلع‬‫الذي‬‫جميع‬‫زواياه‬
‫وجميع‬ ......................‫أضلهعه‬....................
3-‫عدد‬ ‫الذي‬ ‫المنتظم‬ ‫المضلع‬ ‫في‬ ‫الداخلة‬ ‫الزاوية‬ ‫قياس‬
= ‫ن‬ ‫اضلعه‬...............
4-................. = ‫مضلع‬ ‫لي‬ ‫الخارجة‬ ‫الزوايا‬ ‫مجموع‬
5-‫الداخلة‬ ‫الزوايا‬ ‫قياسات‬ ‫مجموع‬........... = ‫الرباعي‬ ‫للشكل‬
6-‫الداخلة‬ ‫الزوايا‬ ‫قياسات‬ ‫مجموع‬........... = ‫الخماسي‬ ‫للشكل‬
7-‫الداخلة‬ ‫الزوايا‬ ‫قياسات‬ ‫مجموع‬........... = ‫الخماسي‬ ‫للشكل‬
8-‫المنتظم‬ ‫الخماسي‬ ‫المضلع‬ ‫في‬ ‫الداخلة‬ ‫الزاوية‬ ‫قياس‬....=
9-‫المنتظم‬ ‫الخماسي‬ ‫المضلع‬ ‫في‬ ‫الداخلة‬ ‫الزاوية‬ ‫قياس‬....=
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2‫منتظم‬ ‫لمضلع‬ ‫الخارجة‬ ‫الزاوية‬ ‫قياس‬ ‫كان‬ ‫اذا‬ :
‫يساوي‬305
‫؟‬ ‫الداخله‬ ‫زواياه‬ ‫مجموع‬ ‫وما‬ ‫اضلعه‬ ‫ماعدد‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3‫المقابل‬ ‫الشكل‬ ‫في‬ :‫أ‬ ‫د‬
‫الضلع‬ ‫متساوي‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬805
‫جـ‬ ‫هـ‬ ( ‫هـ‬ > )‫ق‬ ‫أوجد‬

13. 100
5
‫و‬‫ب‬
3‫اللضلع‬ ‫متواي‬ -
‫س‬1‫مايأتي‬ ‫أكمل‬ :
1-............... ‫القطران‬ ‫اللضلع‬ ‫متوازي‬ ‫في‬
2-............ ‫متقابلتان‬ ‫زاويتان‬ ‫كل‬ ‫اللضلع‬ ‫متوازي‬ ‫في‬
3-= ‫متتاليتان‬ ‫زاويتان‬ ‫اي‬ ‫مجموع‬ ‫اللضلع‬ ‫متوازي‬ ‫في‬.....
4-............... ‫يسمى‬ ‫متوازيان‬ ‫لضلعان‬ ‫كل‬ ‫فيه‬ ‫الذي‬ ‫الشكل‬
5-............... ‫يسمى‬ ‫متوازيان‬ ‫لضلعان‬ ‫فيه‬ ‫الذي‬ ‫الشكل‬
6-= (‫أ‬ )‫ق‬ ‫فيه‬ ‫الضلع‬ ‫متوازي‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬50=(‫ق)ب‬ ‫فان‬
7-‫فإن‬ (‫ق)ب‬ ‫نصف‬ (‫أ‬ )‫ق‬ ‫فيه‬ ‫الضلع‬ ‫متوازي‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬
.............. = (‫ق)ب‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2‫أ‬ ‫المقابل‬ ‫الشكل‬ ‫في‬ :6‫د‬ ‫سم‬
‫أوجد‬ ‫الضلع‬ ‫متوازي‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬705
(‫ق)ب‬
( ‫د‬ )‫ق‬ ، (‫جـ‬ )‫ق‬5‫سم‬
‫جـ‬ ‫ب‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫اللضلع‬ ‫متوازي‬ ‫محيط‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3‫المقابل‬ ‫الشكل‬ ‫في‬ :‫أ‬30‫ب‬
‫د‬ ‫جـ‬ // ‫ب‬ ‫أ‬70
‫الشكل‬ ‫أن‬ ‫برهن‬‫الضلع‬ ‫متوازي‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬40
‫د‬ ‫جـ‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬

14. ‫س‬4‫المقابل‬ ‫الشكل‬ ‫في‬ :‫أ‬
‫ب‬
‫الشكل‬ ‫أن‬ ‫برهن‬‫الضلع‬ ‫متوازي‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬4565
70115
4‫والمربع‬ ‫والمعين‬ ‫المستطيل‬ -
‫س‬1‫مايأتي‬ ‫أكمل‬ :
1(‫متوازي‬‫اللضل ع‬‫الذي‬‫إحدى‬‫زواياه‬‫قائمة‬‫يكون‬...........
‫والمعين‬‫الذي‬‫إحدى‬‫زواياه‬‫قائمة‬‫يكون‬..............
2‫متوازي‬ (‫اللضل ع‬‫الذي‬‫قطراه‬‫متساويان‬‫يكون‬، .........
‫متعامدان‬‫يكون‬،............‫متساويان‬‫ومتعامدان‬‫يكون‬.......
3‫المعين‬ (‫الذي‬‫قطراه‬‫متساويان‬....................‫يكون‬
4‫إذا‬ (‫كان‬‫أ‬‫ب‬‫جـ‬‫د‬‫معين‬‫فإن‬..........┴...........
5‫المربع‬ (‫هو‬‫احدى‬ ................‫زواياه‬‫قائمة‬
6‫متوازي‬ (‫اللضل ع‬‫الذي‬‫قطراه‬‫يسمى‬ ............‫مستطيل‬
7‫الشكل‬ (‫الرباعي‬‫الذي‬‫ألضلعه‬‫متساوية‬‫في‬‫الطول‬‫هو‬......
8‫المعين‬ (‫الذي‬‫محيطه‬40‫سم‬‫يكون‬‫طول‬‫لضلعه‬.............
9‫شكل‬ (‫سداسي‬‫منتظم‬‫محيطه‬30‫سم‬‫يكون‬‫طول‬‫لضلعه‬...
10‫(مستطيل‬‫محيطه‬20‫سم‬‫وطوله‬6‫سم‬‫فإن‬‫عرلضه‬.... =
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2‫المقابل‬ ‫الشكل‬ ‫في‬ :‫د‬ ‫أ‬
‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬(‫أ‬ )‫ق‬ ‫بالبرهان‬ ‫أوجد‬ ‫معين‬
5
62
‫ب‬‫جـ‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3‫المقابل‬ ‫الشكل‬ ‫في‬ :‫د‬ ‫أ‬ :
‫هـ‬ ‫د‬ // ‫جـ‬ ‫أ‬ ، ‫مربع‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬

15. 1( ‫هـ‬ ‫جـ‬ ‫أ‬ )‫ق‬ ‫أوجد‬ -
2‫ألضلع‬ ‫متوازي‬ ‫د‬ ‫هـ‬ ‫جـ‬ ‫أ‬ ‫أن‬ ‫اثبت‬ -
‫هـ‬ ‫جـ‬ ‫ب‬
5‫المثلث‬ -
‫س‬1‫مايأتي‬ ‫أكمل‬ :
1(= ‫للمثلث‬ ‫الداخلة‬ ‫الزوايا‬ ‫قياسات‬ ‫مجموع‬......
2(‫تساوي‬ ‫المثلث‬ ‫عن‬ ‫خارجة‬ ‫زاوية‬ ‫أي‬ ‫قياس‬
‫مجموع‬.................................
3(‫زاويتان‬ ‫على‬ ‫يحتوي‬ ‫مثلث‬ ‫أي‬.‫اللقل‬ ‫على‬ .......
4(‫مجموع‬ ‫مثلث‬ ‫في‬ ‫زاوية‬ ‫قياس‬ ‫ساوى‬ ‫إذا‬
‫كان‬ ‫الخرتان‬ ‫الزاويتان‬............. ‫المثلث‬
5((‫ب‬ )‫ق‬ + (‫ق)أ‬ ‫كان‬ ‫إذا‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫في‬
(‫جـ‬ )‫ق‬ ‫فإن‬ (‫جـ‬ )‫ق‬ =.........=
6((‫ب‬ )‫ق‬ + (‫ق)أ‬ ‫كان‬ ‫إذا‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫في‬
=110.......... = (‫جـ‬ )‫ق‬ ‫فإن‬
7(.... = ‫اللضلع‬ ‫المتساوي‬ ‫المثلث‬ ‫في‬ ‫زاوية‬ ‫كل‬ ‫قياس‬
8(‫المتساوي‬ ‫المثلث‬ ‫عن‬ ‫الخارجة‬ ‫الزاوية‬ ‫قياس‬
.... = ‫اللضلع‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2‫د‬ ‫أ‬ ‫المقابل‬ ‫الشكل‬ ‫في‬
= (‫جـ‬ ‫أ‬ ‫د‬ )‫ق‬ ‫جـ‬ ‫ب‬ // ‫د‬ ‫أ‬605
،
= ( ‫د‬ ‫أ‬ ‫ب‬ )‫ق‬1305
(‫ق)جـ‬ ، (‫ب‬ )‫ق‬ ‫أوجد‬
‫جـ‬ ‫ب‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬

16. ‫س‬3= (‫ق)أ‬ :‫المقابل‬ ‫الشكل‬ ‫في‬ :505
‫أ‬
= (‫ق)ب‬ ،605
(‫د‬ ‫أجـ‬ )‫ق‬ ‫أوجد‬
‫ب‬ ‫جـ‬ ‫د‬
6‫المستقيمة‬ ‫والقطعه‬ ‫الشعاع‬ ‫نظرية‬ -
‫س‬1‫مايأتي‬ ‫أكمل‬ :
1(‫أحد‬ ‫موازيا‬ ‫مثلث‬ ‫من‬ ‫لضلع‬ ‫منتصف‬ ‫من‬ ‫المرسوم‬ ‫الشعاع‬
‫الخرين‬ ‫الضلعين‬...........
2(‫مثلث‬ ‫في‬ ‫لضلعين‬ ‫منتصفي‬ ‫بين‬ ‫المرسومة‬ ‫المستقيمة‬ ‫القطعة‬
...............................
3(‫فإن‬ ‫أخر‬ ‫مثلث‬ ‫في‬ ‫زاويتان‬ ‫مثلث‬ ‫في‬ ‫زاويتان‬ ‫ساوى‬ ‫إذا‬
‫الول‬ ‫المثلث‬ ‫في‬ ‫الزاويةالثالثة‬...............
4(‫جـ‬ ‫ب‬ ، ‫جـ‬ ‫أ‬ ‫منتصف‬ ‫هـ‬ ، ‫أب‬ ‫منتصف‬ ‫د‬ ‫فيه‬ ‫مثلث‬ ‫جـ‬ ‫ب‬ ‫أ‬
=10= ‫دهـ‬ ‫فإن‬ ‫سم‬........
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2:‫أ‬ ‫منتصفات‬ ‫ع‬ ، ‫ص‬ ، ‫س‬ ‫المقابل‬ ‫الشكل‬ ‫في‬
‫ص‬ ‫س‬ ‫الترتيب‬ ‫على‬ ‫جـ‬ ‫،أ‬ ‫جـ‬ ‫ب‬ ، ‫أب‬ ‫اللضلع‬
= ‫أب‬6= ‫جـ‬ ‫ب‬ ، ‫سم‬8= ‫أجـ‬ ، ‫سم‬10‫سم‬
‫ع‬ ‫ص‬ ‫س‬ ‫المثلث‬ ‫محيط‬ ‫أوجد‬‫جـ‬ ‫ع‬ ‫ب‬
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3‫المقابل‬ ‫الشكل‬ ‫في‬ :‫أ‬ :
‫جـ‬ ‫أ‬ ‫منتصف‬ ‫هـ‬ ، ‫ب‬ ‫أ‬ ‫منتصف‬ ‫د‬
= ‫جـ‬ ‫ب‬ ، ‫و‬ ‫د‬ ‫منتصف‬ ‫س‬12‫سم‬‫هـ‬ ‫د‬
‫ص‬ ‫س‬ ، ‫هـ‬ ‫د‬ ‫طول‬ ‫أوجد‬

17. ‫ب‬‫ص‬ ‫س‬‫جـ‬
‫و‬
7‫فيثاغورث‬ ‫نظرية‬ -
‫س‬1‫مايأتي‬ ‫أكمل‬ :
1‫في‬ (‫المثلث‬‫القائم‬‫مربع‬‫طول‬‫الوتر‬‫يساوي‬‫مجمو ع‬‫مربعي‬
.....................
2-‫في‬‫المثلث‬‫القائم‬‫مساحة‬‫المربع‬‫المنشأ‬‫على‬‫الوتر‬‫يساوي‬
‫مجمو ع‬‫مساحتي‬‫المربعين‬‫المنشأين‬‫على‬...........
3‫أ‬ (‫ب‬‫جـ‬‫مثلث‬‫قائم‬‫الزاوية‬‫في‬‫ب‬‫فيه‬‫أ‬‫ب‬=3‫سم‬،‫ب‬‫جـ‬=4
‫سم‬،‫فإن‬‫أ‬‫جـ‬..... =
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2:‫المقابل‬ ‫الشكل‬ ‫في‬‫أ‬
‫جـ‬ ‫أ‬ ‫طول‬ ‫أوجد‬6‫سم‬
‫جـ‬ ‫ب‬
‫ــــــــــــــــــــــــــــــــــــــــ‬8‫سم‬
‫س‬3:‫المقابل‬ ‫الشكل‬ ‫في‬‫أ‬
‫جـ‬ ‫ب‬ ‫طول‬ ‫أوجد‬5‫سم‬13‫سم‬
‫جـ‬ ‫ب‬
‫ــــــــــــــــــــــــــــــــــ‬
‫س‬4:‫جـ‬ ‫ب‬ ┴ ‫د‬ ‫أ‬ :‫المقابل‬ ‫الشكل‬ ‫في‬‫أ‬
‫جـ‬ ‫ب‬ ‫أوجد‬13‫سم‬12‫سم‬15‫سم‬

18. ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫مساحة‬ ‫واحسب‬
‫جـ‬ ‫د‬ ‫ب‬
8‫النعكاس‬ -
‫س‬1‫مايأتي‬ ‫أكمل‬ :
1) ‫النقطة‬ ‫صور‬ (1،3...... ‫هي‬ ‫السينات‬ ‫محور‬ ‫في‬ ‫بالنعكاس‬ (
2) ‫النقطة‬ ‫صور‬ (2- ،7.... ‫هي‬ ‫الصادات‬ ‫محور‬ ‫في‬ ‫بالنعكاس‬ (
3) ‫النقطة‬ ‫صور‬ (1- ،5...... ‫هي‬ ‫الصل‬ ‫نقطة‬ ‫في‬ ‫بالنعكاس‬ (
4(.......... ‫على‬ ‫يحافظ‬ ‫مستقيم‬ ‫في‬ ‫النعكاس‬
5(.......... ‫على‬ ‫يحافظ‬ ‫نقطة‬ ‫في‬ ‫النعكاس‬
6...... = ‫المستطيل‬ ، ..... = ‫المربع‬ ‫تماثل‬ ‫محاور‬ ‫عدد‬ (
.....= ‫الساقين‬ ‫المتساوي‬ ‫المثلث‬ ، ، ......= ‫اللضلع‬ ‫المتساوي‬ ‫المثلث‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2= ‫ب‬ ‫أ‬ ‫فيه‬ ‫الذي‬ ‫جـ‬ ‫أب‬ ‫المثلث‬ ‫ارسم‬ :3= ‫جـ‬ ‫ب‬ ، ‫سم‬4، ‫سم‬
= ‫جـ‬ ‫أ‬5‫صورته‬ ‫أوجد‬ ‫ثم‬ ‫سم‬
1-‫لضلع‬ ‫أصغر‬ ‫يحتوي‬ ‫الذي‬ ‫المستقيم‬ ‫في‬ ‫بالنعكاس‬
2-‫جـ‬ ‫النقطة‬ ‫في‬ ‫بالنعكاس‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3) ‫أ‬ ‫حيث‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫ارسم‬ : :1،1)‫ب‬ ، (5،1(
) ‫جـ‬3،5‫السينات‬ ‫ر‬ ‫محو‬ ‫في‬ ‫بالنعكاس‬ ‫صورته‬ ‫أوجد‬ ‫ثم‬ (

19. ‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬4) ‫أ‬ ‫حيث‬ ‫ب‬ ‫أ‬ ‫ارسم‬ :1،2)‫ب‬ ، (3،5‫صورتها‬ ‫أوجد‬ ‫ثم‬ (
‫بالعنعكاس‬1‫الصادات‬ ‫ر‬ ‫محو‬ ‫في‬ -2‫الصل‬ ‫عنقطة‬ -
9‫العنتقال‬ -
‫س‬1‫مايأتي‬ ‫أكمل‬ :
1) ‫النقطة‬ ‫صور‬ (1،3) ‫بالعنتقال‬ (2،4...... ‫هي‬ (
2) ‫النقطة‬ ‫صور‬ (1،3+ ‫س‬ ) ‫بالعنتقال‬ (2- ‫ص‬ ،3...... ‫هي‬ (
3) ‫النقطة‬ ‫صور‬ (2،5‫بالعنتقال‬ (3‫الموجب‬ ‫التجاه‬ ‫في‬ ‫وحدات‬
...... ‫هي‬ ‫السينات‬ ‫لمحور‬
4(.......... ‫على‬ ‫يحافظ‬ ‫على‬ ‫يحافظ‬ ‫المستوى‬ ‫في‬ ‫العنتقال‬
5() ‫بالعنتقال‬ .......... ‫النقطة‬ ‫صور‬2،4) ‫هي‬ (5،8(
6................ ،.............. ‫علم‬ ‫اذا‬ ‫العنتقال‬ ‫يتحدد‬ (
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2= ‫ب‬ ‫أ‬ ‫فيه‬ ‫الذي‬ ‫جـ‬ ‫أب‬ ‫المثلث‬ ‫ارسم‬ :4= ‫جـ‬ ‫ب‬ ، ‫سم‬6، ‫سم‬
= ‫جـ‬ ‫أ‬5‫باعنتقال‬ ‫صورته‬ ‫أوجد‬ ‫ثم‬ ‫سم‬3‫ب‬ ‫جـ‬ ‫اتجاه‬ ‫في‬ ‫سم‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3) ‫أ‬ ‫حيث‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫ارسم‬ : :1،1)‫ب‬ ، (5،1(
) ‫جـ‬3،5– ‫س‬ ) ‫بالعنتقال‬ ‫صورته‬ ‫أوجد‬ ‫ثم‬ (5- ‫ص‬ ،3(

20. ‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬4) ‫أ‬ ‫حيث‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المستطيل‬ ‫ارسم‬ : :1،1)‫ب‬ ، (5،1(
) ‫د‬1،4) ‫جـ‬ (5،4) ‫بالعنتقال‬ ‫صورته‬ ‫أوجد‬ ‫ثم‬ (2،3(
10‫الدوران‬ –
‫س‬1‫مايأتي‬ ‫أكمل‬ :
1) ‫النقطة‬ ‫صور‬ (1،3، ‫و‬ ) ‫بالدوران‬ (90...... ‫هي‬ (
2) ‫النقطة‬ ‫صور‬ (1،4، ‫و‬ ) ‫بالدوران‬ (180...... ‫هي‬ (
3- ) ‫النقطة‬ ‫صور‬ (2،3- ، ‫و‬ ) ‫بالدوران‬ (90...... ‫هي‬ (
4() ‫النقطة‬ ‫صور‬1- ،5، ‫و‬ ) ‫بالدوران‬ (270...... ‫هي‬ (
5(.......... ‫على‬ ‫يحافظ‬ ‫المستوى‬ ‫في‬ ‫الدوران‬
6............. ‫أو‬ .............. ‫بزاويه‬ ‫يكون‬ ‫المحايد‬ ‫الدوران‬ (
7................. ‫والسالب‬ .................... ‫يكون‬ ‫الموجب‬ ‫الدوران‬ (
8................ ،........... ، ............. ‫هي‬ ‫الدوران‬ ‫عناصر‬ (
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2‫ضلعه‬ ‫طول‬ ‫الذي‬ ‫الضل ع‬ ‫المتساوي‬ ‫جـ‬ ‫أب‬ ‫المثلث‬ ‫ارسم‬ :
6، ‫أ‬ ) ‫د‬ ‫بالدوران‬ ‫صورته‬ ‫ارسم‬ ‫ثم‬ ، ‫سم‬605
(
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3) ‫أ‬ ‫حيث‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫ارسم‬ : :1،1)‫ب‬ ، (2،3(
) ‫جـ‬4،1، ‫و‬ ) ‫بالدوران‬ ‫صورته‬ ‫أوجد‬ ‫ثم‬ (180(
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬

21. ‫س‬4) ‫أ‬ ‫حيث‬ ‫ب‬ ‫أ‬ ‫ارسم‬ :1،2)‫ب‬ ، (2،5‫صورتها‬ ‫أوجد‬ ‫ثم‬ (
‫بالدوران‬ ‫بالعنعكاس‬1، ‫و‬ ) ‫د‬ -90(
2- ، ‫و‬ ) -90(
‫الجبر‬ ‫لمادة‬ ‫اختبار‬ ‫عنموذج‬
‫س‬1: ‫الوقواس‬ ‫بين‬ ‫من‬ ‫الصحيحة‬ ‫الجابة‬ ‫اختر‬ (
1(- ) ‫للعدد‬ ‫الجمعي‬ ‫المعكوس‬1(6
- ).......... ‫هو‬1،1- ،6،6(
2(52
–42
) .............. =1،3± ،1± ،3(
3(3+2×5) .............. =25،13،30،20(
4(‫العدد‬ ‫عنصف‬28
) ............... ‫هو‬24
،27
،29
،26
(
5(35
+35
+35
) ................=36
،315
،275
،95
(
6(0.000073=7.3×10‫ن‬
) ....= ‫ن‬ ‫فإن‬5- ،5،6- ،6(
7(62
+82
=6) ......... +8،5،4،3(
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2: ‫يأتي‬ ‫ما‬ ‫أكمل‬ :
1(7‫س‬-4
=7)2(12...........=
........4
3= ‫س‬ ‫كان‬ ‫إذا‬ (1- = ‫ص‬ ،1‫س‬ ‫فإن‬‫ص‬
............ =
3
4(81................ =
6(4500000=4.5........ ×.
7‫)س‬ (5
(3
.............. =
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3:(‫)أ‬‫صورة‬ ‫لبسط‬ ‫اختصر‬:3-4
×37
33
: ‫صورة‬ ‫لبسط‬ ‫اختصر‬ (‫)ب‬16) ×3(2
) +1(‫صفر‬
944
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬4: ‫المتباينة‬ ‫حل‬ ‫مجموعة‬ ‫أوجد‬ (‫)أ‬ :3– ‫س‬45‫ن‬ ‫في‬
: ‫المعادلة‬ ‫حل‬ ‫مجموعة‬ ‫أوجد‬ (‫)ب‬2+ ‫س‬1=9‫ن‬ ‫في‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬5= ‫أ‬ ‫كان‬ ‫إذا‬ (‫)أ‬ :5= ‫ب‬ ،3+ ‫ب‬ ‫أ‬ ‫وقيمة‬ ‫أوجد‬2– ‫أ‬3‫ب‬

22. ‫به‬ ‫كيس‬ (‫)ب‬3، ‫حمراء‬ ‫كرات‬4، ‫بيضاء‬6‫احتمال‬ ‫أوجد‬ ‫عشوائيا‬ ‫كرة‬ ‫سحبت‬ ‫زروقاء‬
‫تكون‬ ‫ان‬1‫حمراء‬ -2‫زروقاء‬ ‫أو‬ ‫حمراء‬ -3‫حمراء‬ ‫ليست‬ -4‫سوداء‬ -
‫الهندسة‬ ‫لمادة‬ ‫اختبار‬ ‫عنموذج‬
‫س‬1:: ‫يأتي‬ ‫ما‬ ‫أكمل‬
1‫تساوي‬ ‫عنقطة‬ ‫حول‬ ‫المتجمعة‬ ‫الزوايا‬ ‫وقياسات‬ ‫مجمو ع‬............
2-............. ‫يكون‬ ‫متعامدان‬ ‫وغير‬ ‫متساويان‬ ‫وقطراه‬ ‫الذي‬ ‫الضل ع‬ ‫متوازي‬
3..........= ‫أضل ع‬ ‫متوازي‬ ‫في‬ ‫متتاليتان‬ ‫زاويتان‬ ‫أي‬ ‫مجمو ع‬ -
4.................................‫تساوي‬ ‫المثلث‬ ‫عن‬ ‫خارجة‬ ‫زاوية‬ ‫أي‬ ‫-وقياس‬
5‫فيه‬ ‫مثلث‬ ‫جـ‬ ‫ب‬ ‫-أ‬=(‫ق)جـ‬ = (‫ق)أ‬405
.............= (‫ب‬ ) ‫ق‬ ‫فإن‬
6.................... = ‫سداسي‬ ‫مضلع‬ ‫لي‬ ‫الخارجة‬ ‫الزوايا‬ ‫-مجمو ع‬
7) ‫النقطة‬ ‫-صورة‬3،5‫بالدوران‬ (905
................. ‫الصل‬ ‫عنقطة‬ ‫حول‬
8) ‫النقطة‬ ‫-صورة‬2- ،1.................... ‫الصل‬ ‫عنقطة‬ ‫في‬ ‫بالعنعكاس‬ (
9-............. ‫مثلث‬ ‫في‬ ‫ضلعين‬ ‫منتصفي‬ ‫بين‬ ‫المرسومة‬ ‫المستقيمة‬ ‫القطعة‬
‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬2:‫أ‬ ‫منتصفات‬ ‫ ع‬ ، ‫ص‬ ، ‫س‬ ‫المقابل‬ ‫الشكل‬ ‫في‬
‫ ع‬ ‫الترتيب‬ ‫على‬ ‫جـ‬ ‫،أ‬ ‫جـ‬ ‫ب‬ ، ‫أب‬ ‫الضل ع‬
= ‫أب‬5= ‫جـ‬ ‫ب‬ ، ‫سم‬12= ‫أجـ‬ ، ‫سم‬13‫سم‬
‫ ع‬ ‫ص‬ ‫س‬ ‫المثلث‬ ‫محيط‬ ‫أوجد‬‫ص‬ ‫جـ‬
) ‫أ‬ ‫حيث‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫ارسم‬ (‫ب‬ )2،1) ) ‫ب‬ ، (3،3) ‫جـ‬ (6،1(
+ ‫س‬ ) ‫بالعنتقال‬ ‫صورته‬ ‫أوجد‬ ‫ثم‬2+ ‫ص‬ ،4(
‫ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬3:‫المقابل‬ ‫الشكل‬ ‫في‬‫د‬ ‫أ‬
‫د‬ ‫أ‬ ، ‫جـ‬ ‫أ‬ ‫طول‬ ‫أوجد‬
3‫سم‬13‫سم‬
‫جـ‬ ‫ب‬
4‫سم‬
‫س‬4) ‫أ‬ ‫حيث‬ ‫د‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المستطيل‬ ‫ارسم‬ : :2،2)‫ب‬ ، (5،2(
) ‫د‬2،4) ‫جـ‬ (5،4- ، ‫و‬ ) ‫بالدوران‬ ‫صورته‬ ‫أوجد‬ ‫ثم‬ (90(

23. ‫ــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ‬
‫س‬4) ‫أ‬ ‫حيث‬ ‫جـ‬ ‫ب‬ ‫أ‬ ‫المثلث‬ ‫ارسم‬ ( ‫أ‬ ) :1،1) ) ‫ب‬ ، (3،1(
) ‫جـ‬2،4‫صورته‬ ‫أوجد‬ ‫ثم‬ (1‫السينات‬ ‫محور‬ ‫في‬ ‫بالعنعكاس‬ -
2‫الصل‬ ‫عنقطة‬ ‫في‬ ‫بالعنعكاس‬ -