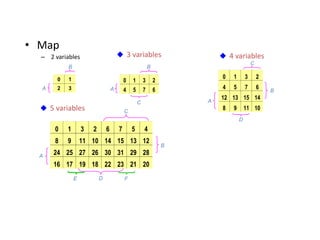
The document provides an in-depth introduction to digital logic circuits, covering the basics of digital computers, hardware and software components, and the principle of binary representation. It explains key concepts such as logic gates, Boolean algebra, and methods for simplifying Boolean expressions, including the use of truth tables and Karnaugh maps. Additionally, it discusses both canonical and standard forms of Boolean functions and their conversion techniques.

1. 1. Introduction to Digital
Logic Circuits
Chapter One

2. Outline

3. 1.1 Digital Computers
• The word digital implies information in computers is represented by
variables that take a limited number of discrete values.
• Ex. Decimal digits 0, 1, …, 9 provide ten discrete values.
• These values are processed by the internal component that can maintain
these values.(1940).
• Digital computers function if only two states are used. Because physical
restrictions of the components that are used restrict us to two states:(
true/false on/off yes/no high/low 0/1 )
• Human logic also tends to these two states
• The two values are said to be binary digits or bits.
• Groups of bits can represent binary numbers, decimal digits, or letters and
instructions.

4. 1.1.1 Computer system
• Divided into two functional entities: hardware and software
• Hardware: consists of all electronic and electromechanical devices.
• Software: Sequences of instructions and data to be manipulated
– Divided in to system and application software
• System : ex. OS: to translate high level language to machine language to be
used by the hardware(compiler)
• Application :written to solve particular problem
• Program: sequence of instructions fro a particular task
• Database : the data that are manipulated by the program

5. Cont’d…
Computer Hardware Divided in to 3 Major Parts:
• CPU:
– Contains ALU for data manipulation
– Contains registers to store data
– Contains control circuits(CU) for fetching and executing instructions
• Memory: Stores instructions and data. It is called RAM
because CPU can access any location in memory at
random and retrieve the binary info within a fixed
interval of time.
• Input/output processor(IOP) : consists electronic
circuits to control transfer and communication of
information between computer and outside world(I/O
devices). e.g. keyboard, printer, scanner, mass storage,
etc.

6. Cont’d…

7. 1.1.2 Three views of computer
hardware:
• Computer organization: concerned with the way
hardware components operate and connect
together to form computer system.
• Computer design: concerned with the hardware
design of the hardware based upon some specs
• Computer architecture: the structure and
behaviour of the computer perceived by the user.
Includes instruction format, instruction set, and
techniques for addressing memory.

8. 1.2 Logic Gates
• Binary information are represented by physical quantities called signals
• ADC(Analog to Digital Conversion)
– Signal Physical Quantity Binary Information
Discrete Value
• Gate
– The manipulation of binary information is done by logic circuit called “gate”.
– Gates are block of hardware that produces ether 0 or 1 based on the input
Digital Logic Gates
– AND, OR, INVERTER, BUFFER, NAND, NOR, XOR, XNOR
– Input output relationship of variables for each gates can be represented by truth table
0 : 0.5
1 : 3

9. Cont…

10. Cont…

11. Cont…

12. 1.3 Boolean Algebra
• Boolean Algebra
– Deals with binary variable(A, B, x, y: T/F or 1/0) + logic operation(AND, OR, NOT…)
– The 3 basic logic operations are AND , OR and complement
• Boolean Function: variable + operators (logical)
– F(x, y, z) = x + y’z
 Truth Table:
 Relationship between a
function and variable
x y z F
0 0 0 0
0 0 1 1
0 1 0 0
0 1 1 0
1 0 0 1
1 0 1 1
1 1 0 1
1 1 1 1
 Logic Diagram:
 Algebraic Expression Logic Diagram
2n Combination
Variable n = 3
x
y
z
F

13. • Purpose of Boolean Algebra
– To facilitate the analysis and design of digital circuit
• Convenient Tools
– Truth table : relationship between binary variables
– Logic diagram : input-output relationship
– Find simpler circuits for the same function
• Boolean Algebra Rule : Tab. 1-1
- Operation with 0 and 1: x + 0 = x , x + 1 = 1 , x • 1 = x , x • 0 = 0
- Idempotent Law: x + x =x , x • x = x
- Complementary Law: x + x' = 1 , x • x' = 0
- Commutative Law: x + y = y + x , x • y = y • x
- Associative Law: x + (y + z) = (x + y) + z , x • ( y • z) = (x • y) • z
- Distributive Law: x • ( y + z) = (x • y) + (x • z) , x + (y • z) = (x + y)•(x + z)
- DeMorgan's Law: (x + y)' = x' • y’ , (x • y )’ = x’ + y’
General Form: (x1 + x2 + x3 + … xn)' = x1' • x2' • x3' • … xn’
(x1 • x2 • x3 • … xn) ' = x1' + x2' + x3'+ … xn’
c
c
c
B
A
B
A 
 
)
(

14. • []
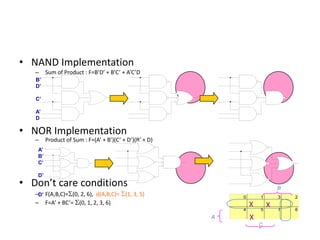
– F= AB’ + C’D + AB’ + C’D
= x + x (let x= AB’ + C’D)
= x
= AB’ + C’D
 []
 F= ABC + ABC’ + A’C
= AB(C + C’) + A’C
= AB + A’C
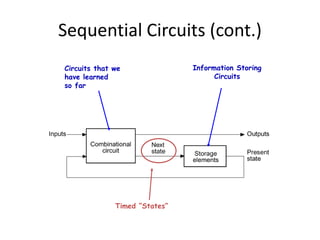
 Fig. 1-4 2 graphic symbols for NOR gate
(a) OR-invert (b) invert-OR
 Fig. 1-5 2 graphic symbols for NAND gate
(a) NAND-invert (b) invert-NAND
(x+y+z)’
x
y
z
x
y
z
x
y
z
x
y
z
(x’+y’+z’)
(xyz)’
x’ y’z’

15. Definitions
• Literal: A variable or its complement
• Product term: literals connected by •
• Sum term: literals connected by +
• Minterm: a product term in which all the variables
appear exactly once, either complemented or
uncomplemented
• Maxterm: a sum term in which all the variables
appear exactly once, either complemented or
uncomplemented

16. Minterm
• Product of one combination in the truth table.
• Denoted by mj, where j is the decimal equivalent of
the minterm’s corresponding binary combination (bj).
• Example: Assume 3 variables (A,B,C), and j=3. Then, bj
= 011 and its corresponding minterm is denoted by mj
= A’BC
 ( x=1, x’=0)

17. Maxterm
• Sum of one combination in the truth table.
• Denoted by Mj, where j is the decimal equivalent of
the maxterm’s corresponding binary combination (bj).
• Example: Assume 3 variables (A,B,C), and j=3. Then, bj
= 011 and its corresponding maxterm is denoted by
Mj = A+B’+C’
 (x=0, x’=1)

18. 1-4 Minterm/Maxterm
• 2 variables example
• F = x’y + xy
x y Minterm Maxterm
0 0 x'y' m0 x + y M0
0 1 x'y m1 x + y' M1
1 0 x y' m2 x'+ y M2
1 1 x y m3 x'+ y' M3
m0 + m1 + m2 + m3 M0  M1  M2 
M3
m1 m3
)
2
,
0
(
)
3
,
1
(




(Complement = M0  M2 )
( m1 + m3 )

19. Canonical SOP/POS
• Truth table for f1(a,b,c) at right
• The canonical sum-of-products form for f1
is:
f1(a,b,c) = m1 + m2 + m4 + m6
= a’b’c + a’bc’ + ab’c’ + abc’
• The canonical product-of-sums form for f1 is
f1(a,b,c) = M0 • M3 • M5 • M7
= (a+b+c)•(a+b’+c’)•
(a’+b+c’)•(a’+b’+c’).
• Observe that: mj = Mj’
a b c f1
0 0 0 0
0 0 1 1
0 1 0 1
0 1 1 0
1 0 0 1
1 0 1 0
1 1 0 1
1 1 1 0

20. Conversion Between Canonical Forms
• Replace ∑ with ∏ (or vice versa) and replace those j’s that
appeared in the original form with those that do not.
• Example:
f1(a,b,c) = a’b’c + a’bc’ + ab’c’ + abc’
= m1 + m2 + m4 + m6
= ∑(1,2,4,6)
= ∏(0,3,5,7)
= (a+b+c)•(a+b’+c’)•(a’+b+c’)•(a’+b’+c’)

21. Standard Forms (NOT Unique)
• In Standard forms ,not all variables need to appear in
the individual product (SOP) or sum (POS) terms.
• Example:
f1(a,b,c) = a’b’c + bc’ + ac’
is a standard sum-of-products form
• f1(a,b,c) = (a+b+c)•(b’+c’)•(a’+c’)
is a standard product-of-sums form.

22. Conversion of SOP from standard to
canonical form
• Expand non-canonical terms by inserting equivalent of
1 in each missing variable x:
(x + x’) = 1
• Remove duplicate minterms
• f1(a,b,c) = a’b’c + bc’ + ac’
= a’b’c + (a+a’)bc’ + a(b+b’)c’
= a’b’c + abc’ + a’bc’ + abc’ + ab’c’
= a’b’c + abc’ + a’bc + ab’c’

23. Conversion of POS from standard to
canonical form
• Expand noncanonical terms by adding 0 in terms of
missing variables (e.g., xx’ = 0) and using the
distributive law
• Remove duplicate maxterms
• f1(a,b,c) = (a+b+c)•(b’+c’)•(a’+c’)
= (a+b+c)•(aa’+b’+c’)•(a’+bb’+c’)
= (a+b+c)•(a+b’+c’)•(a’+b’+c’)•
(a’+b+c’)•(a’+b’+c’)
= (a+b+c)•(a+b’+c’)•(a’+b’+c’)•(a’+b+c’)

24. Karnaugh Maps simplification
• Karnaugh maps (K-maps) are graphical
representations of boolean functions.
• Also, one map cell corresponds to a minterm or a
maxterm in the boolean expression
• Any two adjacent cells in the map differ by ONLY one
variable, which appears complemented in one cell
and uncomplemented in the other.
• Example:
m0 (=x1’x2’) is adjacent to m1 (=x1’x2) and m2 (=x1x2’)
but NOT m3 (=x1x2)

25. K-map
• Enter 1s in the K-map for each product term in the
function
• Group adjacent K-map cells containing 1s to obtain a
product with fewer variables. Group size must be in
power of 2 (2, 4, 8, …)
• Handle “boundary wrap” for K-maps of 3 or more
variables.
• Realize that answer may not be unique

26. Simplification
• Enter minterms of the Boolean function into
the map, then group terms
• Example: f(a,b,c) = a’c + abc + bc’
• Result: f(a,b,c) = a’c+ b
1 1 1
1 1
a
bc
1 1 1
1 1

27. More Examples
• f1(x, y, z) = ∑ m(2,3,5,7)
• f2(x, y, z) = ∑ m (0,1,2,3,6)
 f1(x, y, z) = x’y + xz
f2(x, y, z) = x’+yz’
yz
X 00 01 11 10
0 1 1
1 1 1
1 1 1 1
1

28. • Map
– 2 variables  3 variables  4 variables
0 1
2 3
A
B B
0 1 3 2
4 5 7 6
A
C A
0 1 3 2
4 5 7 6
12 13 15 14
8 9 11 10
B
C
D
 5 variables
0 1 3 2 6 7 5 4
8 9 11 10 14 15 13 12
24 25 27 26 30 31 29 28
16 17 19 18 22 23 21 20
A
B
C
D F
E

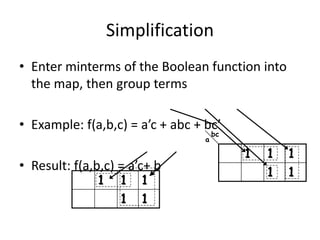
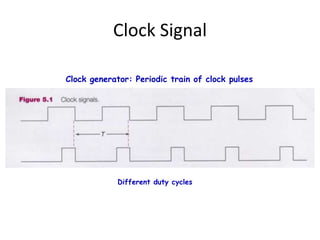
29. • [] F= x + y’z
(1) Truth Table
x y z F Minterm
0 0 0 0 m0
0 0 1 1 m1
0 1 0 0 m2
0 1 1 0 m3
1 0 0 1 m4
1 0 1 1 m5
1 1 0 1 m6
1 1 1 1 m7
(2) )
7
,
6
,
5
,
4
,
1
(
)
,
,
( 

z
y
x
F
(3)
z
x
y
0 1 3 2
4 5 7 6
F= x + y’z

30. • Adjacent Square
– Number of square = 2n (2, 4, 8, ….)
– The squares at the extreme ends of the
same horizontal row are to be considered
adjacent
– The same applies to the top and bottom
squares of a column
– The four corner squares of a map must be
considered to be adjacent
– Groups of combined adjacent squares may
share one or more squares with one or
more group
0 1 3 2
4 5 7 6
0 1 3 2
4 5 7 6
12 13 15 14
8 9 11 10
0 1 3 2
4 5 7 6
0 1 3 2
4 5 7 6
12 13 15 14
8 9 11 10
0 1 3 2
4 5 7 6

31. • []
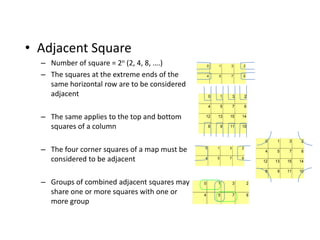
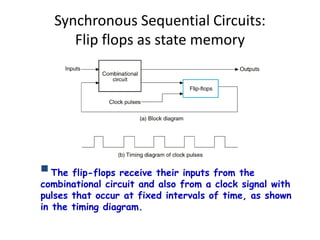
– F=AC’ + BC
)
7
,
6
,
4
,
3
(
)
,
,
( 

C
B
A
F
 []
 F=C’ + AB’
)
6
,
5
,
4
,
2
,
0
(
)
,
,
( 

C
B
A
F
B
0 1 3 2
4 5 7 6
A
C B
0 1 3 2
4 5 7 6
A
C
A
0 1 3 2
4 5 7 6
12 13 15 14
8 9 11 10
B
C
D
 []
 F=C’ + AB’
)
10
,
9
,
8
,
6
,
2
,
1
,
0
(
)
,
,
,
( 

D
C
B
A
F
A
0 1 3 2
4 5 7 6
12 13 15 14
8 9 11 10
B
C
D
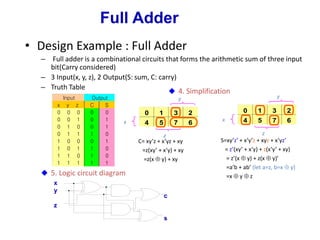
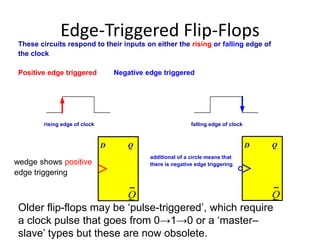
 Product-of-Sums Simplification
F=B’D’ + B’C’ + A’C’D
F’=AB + CD + BD’(square marked 0’s)
F’’(F)=(A’ + B’)(C’ + D’)(B’ + D)
)
10
,
9
,
8
,
5
,
2
,
1
,
0
(
)
,
,
,
( 

D
C
B
A
F
Sum of product
Product of Sum

32. • NAND Implementation
– Sum of Product : F=B’D’ + B’C’ + A’C’D
• NOR Implementation
– Product of Sum : F=(A’ + B’)(C’ + D’)(B’ + D)
• Don’t care conditions
– F(A,B,C)=(0, 2, 6), d(A,B,C)= (1, 3, 5)
– F=A’ + BC’= (0, 1, 2, 3, 6)
B’
D’
C’
A’
D
A’
B’
C’
D’
D’
A
B
0 1 3 2
4 5 7 6
C
X
X
X

33. Don't Care Conditions
• 0’s and 1’s in the map represent minterms that produce
1or 0 for the function.
• Some times we don’t care what the function produce.
• The minterms that may produce either 0 or 1 for the
function are said to be don't care conditions.
• They are denoted with x or –.
• Don’t cares can be used to further simplify the algebraic
expression by enclosing max number of squares(X and 1) .

34. • Simplify the function F(A,B,C)
whose K-map is shown at the right.
• The simplified expression is:
• If it is simplified w/o don’t cares the
expression will be :
• Consider no/type of gate we require
in both cases.
Combining 1’s and x
we get

35. 1-5 Combinational Circuits
• Combinational Circuits
– A connected arrangement of logic gates with a set of inputs and outputs
– Fig. 1-15 Block diagram of a combinational circuit
• Analysis
– Logic circuits diagram Boolean function or Truth table
• Design(Analysis )
– 1. The Problem is stated
– 2. I/O variables are assigned
– 3. Truth table(I/O relation)
– 4. Simplified Boolean Function
– 5. Logic circuit diagram
i0
i1
in
f0
f1
fm
.
.
.
.
.
.
Combinational
Circuits
(Logic Gates)
Experience

36. Half-Adder:
A combinational circuit which adds two one-bit binary
numbers is called a half-adder.
o The sum column resembles like an output of the XOR gate.
o The carry column resembles like an output of the AND
gate.

37. • Design Example : Full Adder
– Full adder is a combinational circuits that forms the arithmetic sum of three input
bit(Carry considered)
– 3 Input(x, y, z), 2 Output(S: sum, C: carry)
– Truth Table
Input
x y z C S
0 0 0 0 0
0 0 1 0 1
0 1 0 0 1
0 1 1 1 0
1 0 0 0 1
1 0 1 1 0
1 1 0 1 0
1 1 1 1 1
Output
 4. Simplification
y
0 1 3 2
4 5 7 6
x
z
y
0 1 3 2
4 5 7 6
x
z
C= xy’z + x’yz + xy
=z(xy’ + x’y) + xy
=z(x  y) + xy
 5. Logic circuit diagram
S=xy’z’ + x’y’z + xyz + x’yz’
= z’(xy’ + x’y) + z(x’y’ + xy)
= z’(x  y) + z(x  y)’
=a’b + ab’ (let a=z, b=x  y)
=x  y  z
x
y
z
c
s
Full Adder

38. Sequential Circuits
• Combinational circuit:
– Output depends only on current input
– Able to perform useful operations
(add/subtract/multiply/…)
– Has no memory

39. Sequential Circuits (cont.)
• Sequential circuit :
– Output depends not only on current input but also
on past input values, e.g., design a counter
– Need some type of memory to remember the past
input values

40. Sequential Circuits (cont.)
Circuits that we
have learned
so far
Information Storing
Circuits
Timed “States”

41. Sequential Logic: Concept
• Sequential Logic circuits remember past inputs
and past circuit state.
• Outputs from the system are
“fed back” as new inputs
• The storage elements are circuits that are
capable of storing binary information: memory.

42. Synchronous vs. Asynchronous
There are two types of sequential circuits:
• Synchronous sequential circuit: circuit output
changes only at some discrete instants of time. This
type of circuits achieves synchronization by using a
timing signal called the clock.
• Asynchronous sequential circuit: circuit output can
change at any time (clockless).

43. Clock Signal
Different duty cycles
Clock generator: Periodic train of clock pulses

44. Synchronous Sequential Circuits:
Flip flops as state memory
 The flip-flops receive their inputs from the
combinational circuit and also from a clock signal with
pulses that occur at fixed intervals of time, as shown
in the timing diagram.

45. Edge-Triggered Flip-Flops
These circuits respond to their inputs on either the rising or falling edge of
the clock
Positive edge triggered Negative edge triggered
rising edge of clock falling edge of clock
D Q
Q Q
Older flip-flops may be ‘pulse-triggered’, which require
a clock pulse that goes from 0→1→0 or a ‘master–
slave’ types but these are now obsolete.
D Q
wedge shows positive
edge triggering
additional of a circle means that
there is negative edge triggering

46.  JK(Jack/King) F/F
 JK F/F is a refinement of the SR F/F
 The indeterminate condition of the SR type is
defined in complement
1-6 Flip-Flops
 Flip-Flop
 The storage elements employed in clocked sequential circuit
 A binary cell capable of storing one bit of information
 SR(Set/Reset) F/F
Difficult to manage(due to indeterminate state)
Combinational Circuit = Gate
Sequential Circuit = Gate + F/F
Q
Q
SET
CLR
S
R
S R
0 0
0 1
1 0
1 1 ? Indeterminate
Q(t+1)
Q(t) no change
0 clear to 0
1 set to 1
 D(Data) F/F
 “no change” condition : Q(t+1)= Q(t)
1) Disable Clock 2) Feedback
output into input
J
Q
Q
K
SET
CLR
D
0
1
Q(t+1)
0 clear to 0
1 set to 1
J K
0 0
0 1
1 0
1 1 Q(t)' Complement
Q(t+1)
Q(t) no change
0 clear to 0
1 set to 1
Q
Q
SET
CLR
D
 T(Toggle) F/F
 T=1(J=K=1), T=0(J=K=0) JK F/F
 : Q(t+1)= Q(t)  T
Q
Q
SET
CLR
T T
0
1
Q(t+1)
Q(t) no change
Q'(t) Complement

47. Sequential Circuits input equation
• A sequential circuit is an interconnection of F/F and Gate
• Clocked synchronous sequential circuit
• Flip-Flop Input Equation
– Boolean expression for F/F input
– Input Equation
• DA = Ax + Bx, DB = A’x
– Output Equation
• y = Ax’ + Bx’
– Fig. 1-25 Example of a sequential
circuit
Combinational Circuit = Gate
Sequential Circuit = Gate + F/F
Combinational
Circuit
Flip-Flops
Input
Output
Clock
Q
Q
SET
CLR
D
Q
Q
SET
CLR
D
x
DA
DB
A
A’
B
B’
Clock
y

48. Example of state tables
• Present state input Next State Output
• A B x A B y
• 0 0 0 0 0 0
• 0 0 1 0 1 0
• 0 1 0 0 0 1
• 0 1 1 1 1 0
• 1 0 0 0 0 1
• 1 0 1 1 0 0
• 1 1 0 0 0 1
• 1 1 1 1 0 0
State equation:
A(t+1) = DA = Ax + Bx,
B(t+1) = DB = A’x
y(t)= y = Ax’ + Bx’