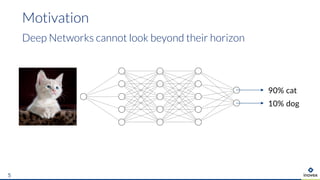
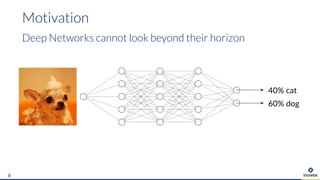
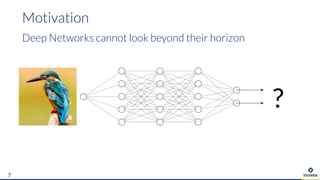
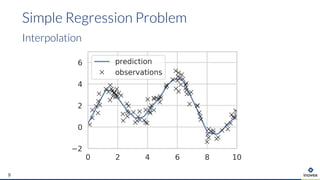
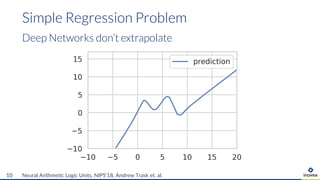
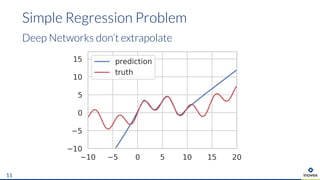
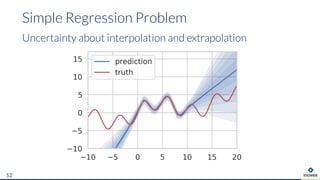
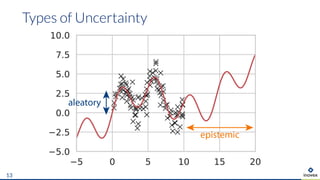
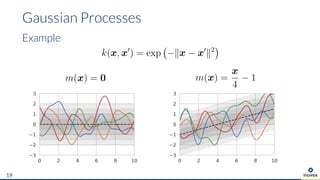
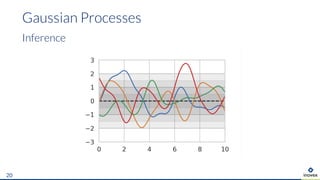
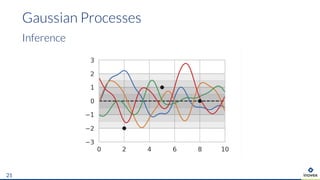
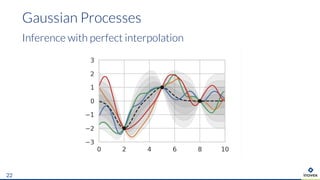
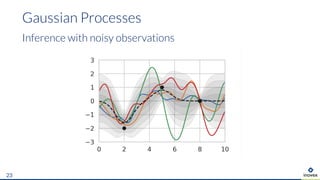
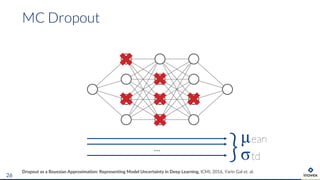
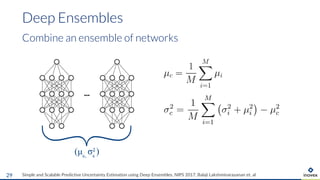
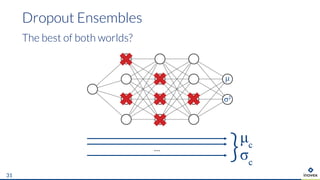
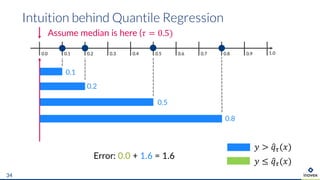
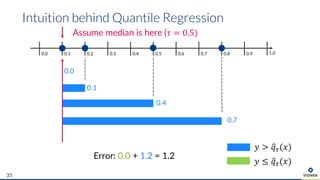
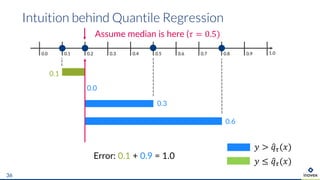
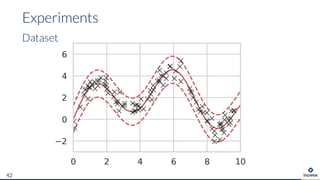
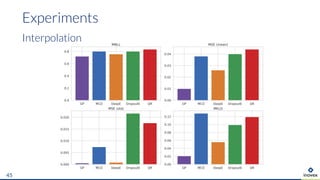
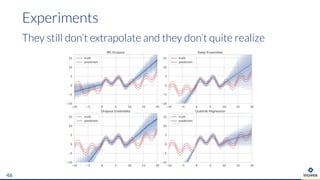
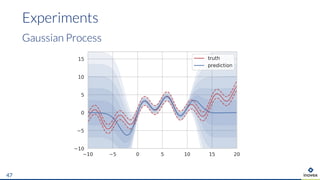
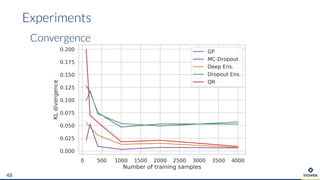
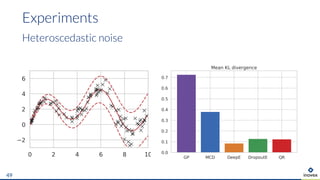
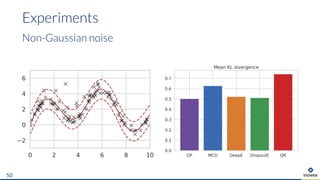
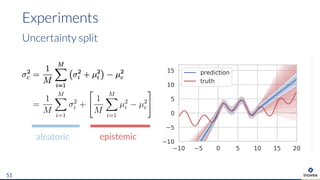
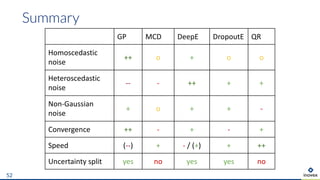
The document presents an overview of uncertainty quantification methods in artificial intelligence, focusing on deep learning techniques such as Gaussian processes, Monte Carlo dropout, and deep ensembles. It discusses the limitations of deep networks in extrapolation and the significance of estimating both aleatory and epistemic uncertainties. The conclusion emphasizes the need for developing combined solutions that effectively address uncertainty estimation in critical applications.

1. Are you sure about that!?
Uncertainty Quantification in AI
Florian Wilhelm Berlin, October 10th 2019

2. 2
Dr. Florian Wilhelm
Principal Data Scientist @ inovex
@FlorianWilhelm
FlorianWilhelm
florianwilhelm.info
Mathematical Modelling
Data Science to Production
Recommender Systems
Uncertainty Quantification & Causality
Python Data Stack
Maintainer PyScaffold

3. 3
Simon Bachstein
Data Scientist @ inovex
2018/07 – 2019/01 Master Thesis at inovex:
Uncertainty Quantification in Deep Learning
• Blogpost:
http://inovex.de/blog/uncertainty-quantification-deep-learning
• Master Thesis:
https://sbachstein.de/master_thesis.pdf
@simonbachstein
sbachstein
sbachstein.de

4. 1. Motivation
2. Methods
a. Gaussian Processes
b. Monte-Carlo Dropout
c. Deep Ensembles
d. Dropout Ensembles
e. Quantile Regression
3. Experiments
4. Conclusion & Outlook
Agenda
4

5. Deep Networks cannot look beyond their horizon
Motivation
5
90% cat
10% dog

6. Deep Networks cannot look beyond their horizon
Motivation
6
40% cat
60% dog

7. Deep Networks cannot look beyond their horizon
Motivation
7
?

8. Boult, T. E., Cruz, S., Dhamija, A., Gunther, M., Henrydoss, J., & Scheirer, W. (2019). Learning and the Unknown: Surveying
Steps Toward Open World Recognition. Aaai, 1–8. Retrieved from www.aaai.org
Learning and the Unknown
8

9. Simple Regression Problem
Interpolation
9

10. Simple Regression Problem
Deep Networks don’t extrapolate
Neural Arithmetic Logic Units, NIPS'18, Andrew Trask et. al.10

11. Simple Regression Problem
Deep Networks don’t extrapolate
11

12. Simple Regression Problem
Uncertainty about interpolation and extrapolation
12

13. Types of Uncertainty
13

14. 1. Motivation
2. Methods
a. Gaussian Processes
b. Monte-Carlo Dropout
c. Deep Ensembles
d. Dropout Ensembles
e. Quantile Regression
3. Experiments
4. Conclusion & Outlook
Agenda
14

15. Methods for Uncertainty Quantification
16
Relaxation of mathematical assumptions about data
Gaussian
Processes
Deep Ensembles / Dropout
Ensembles
Quantile
Regression
Monte Carlo
Dropout

16. 1. Motivation
2. Methods
a. Gaussian Processes
b. Monte-Carlo Dropout
c. Deep Ensembles
d. Dropout Ensembles
e. Quantile Regression
3. Experiments
4. Conclusion & Outlook
Agenda
17

17. A Gaussian Process can be thought of as a random function
which is defined by its mean and covariance functions
Gaussian Processes
18
Definition

18. Gaussian Processes
19
Example

19. Gaussian Processes
20
Inference

20. Gaussian Processes
21
Inference

21. Gaussian Processes
22
Inference with perfect interpolation

22. Gaussian Processes
23
Inference with noisy observations

23. Gaussian Processes
24
Inference
Inference using given data points can be done analytically. For
example, when assuming the (prior) mean function to be zero
everywhere, we get:
Good introduction:
Bayesian Non-parametric Models for Data Science using PyMC by Christopher Fonnesbeck
• https://www.youtube.com/watch?v=-sIOMs4MSuA
• https://de.slideshare.net/mlreview/bayesian-nonparametric-models-for-data-science-using-pymc
computationally intense

24. 1. Motivation
2. Methods
a. Gaussian Processes
b. Monte-Carlo Dropout
c. Deep Ensembles
d. Dropout Ensembles
e. Quantile Regression
3. Experiments
4. Conclusion & Outlook
Agenda
25

25. MC Dropout
Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning, ICML 2016, Yarin Gal et. al.
26
...

26. 1. Motivation
2. Methods
a. Gaussian Processes
b. Monte-Carlo Dropout
c. Deep Ensembles
d. Dropout Ensembles
e. Quantile Regression
3. Experiments
4. Conclusion & Outlook
Agenda
27

27. Deep Ensembles
Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles, NIPS 2017, Balaji Lakshminarayanan et. al28
Custom loss function:
Capture uncertainty directly at training time

28. Deep Ensembles
Simple and Scalable Predictive Uncertainty Estimation using Deep Ensembles, NIPS 2017, Balaji Lakshminarayanan et. al29
Combine an ensemble of networks

29. 1. Motivation
2. Methods
a. Gaussian Processes
b. Monte-Carlo Dropout
c. Deep Ensembles
d. Dropout Ensembles
e. Quantile Regression
3. Experiments
4. Conclusion & Outlook
Agenda
30

30. Dropout Ensembles
31
The best of both worlds?
...

31. 1. Motivation
2. Methods
a. Gaussian Processes
b. Monte-Carlo Dropout
c. Deep Ensembles
d. Dropout Ensembles
e. Quantile Regression
3. Experiments
4. Conclusion & Outlook
Agenda
32

32. Using the cumulative distribution function (cdf) of a random variable Y, we
define the quantile:
Loss function to estimate quantile:
Quantile Regression
33

33. Intuition behind Quantile Regression
34
0.0 0.1 0.2 0.90.3 0.4 0.5 0.6 0.7 0.8 1.0
Assume median is here (𝜏 = 0.5)
𝑦 > )𝑞+(𝑥)
𝑦 ≤ )𝑞+(𝑥)
0.1
0.2
0.5
0.8
Error: 0.0 + 1.6 = 1.6

34. Intuition behind Quantile Regression
35
0.0 0.1 0.2 0.90.3 0.4 0.5 0.6 0.7 0.8 1.0
Assume median is here (𝜏 = 0.5)
𝑦 > )𝑞+(𝑥)
𝑦 ≤ )𝑞+(𝑥)
0.1
0.4
0.7
Error: 0.0 + 1.2 = 1.2
0.0

35. Intuition behind Quantile Regression
36
0.0 0.1 0.2 0.90.3 0.4 0.5 0.6 0.7 0.8 1.0
Assume median is here (𝜏 = 0.5)
𝑦 > )𝑞+(𝑥)
𝑦 ≤ )𝑞+(𝑥)
0.1
0.3
0.6
Error: 0.1 + 0.9 = 1.0
0.0

36. Intuition behind Quantile Regression
37
0.0 0.1 0.2 0.90.3 0.4 0.5 0.6 0.7 0.8 1.0
Assume median is here (𝜏 = 0.5)
𝑦 > )𝑞+(𝑥)
𝑦 ≤ )𝑞+(𝑥)
0.2
0.2
0.5
Error: 0.3 + 0.7 = 1.0
0.1
No change due to the linearity of the error!
+0.1
+0.1
-0.1
-0.1

37. Now the 0.75th Quantile
38
0.0 0.1 0.2 0.90.3 0.4 0.5 0.6 0.7 0.8 1.0
Assume 𝜏 = 0.75 is here
𝑦 > )𝑞+(𝑥)
𝑦 ≤ )𝑞+(𝑥)
0.2
0.2
0.5
0.1
Error: (1 − 0.75) ⋅ 0.3 + 0.75 ⋅ 0.7 = 0.6
Right-side error weights 3 times as much as
the left-side error

38. Now the 0.75th Quantile
39
0.0 0.1 0.2 0.90.3 0.4 0.5 0.6 0.7 0.8 1.0
𝜏 = 0.75
𝑦 > )𝑞+(𝑥)
𝑦 ≤ )𝑞+(𝑥)
0.5
0.1
0.2
Error: (1 − 0.75) ⋅ 1.0 + 0.75 ⋅ 0.2 = 0.4
0.4
Change in the right-side error also weights
3 times as much as the left-side error

39. 1. Motivation
2. Methods
a. Gaussian Processes
b. Monte-Carlo Dropout
c. Deep Ensembles
d. Dropout Ensembles
e. Quantile Regression
3. Experiments
4. Conclusion & Outlook
Agenda
40

40. According to the function
Samples are generated as follows:
Experiments
Uncertainty in Deep Learning (Phd thesis), Yarin Gal, http://mlg.eng.cam.ac.uk/yarin/blog_2248.html41
Dataset

41. Experiments
42
Dataset

42. Neural networks
› 2 hidden layers with 20 ReLU neurons each
› 5 networks for Deep Ensembles
› 100 iterations for Dropout predictions
› Adam optimizer with batch size of 128
› LR, weight decay, dropout probability are optimized
Gaussian Processes
› squared exponential covariance and zero mean function prior
› covariance function parameters and aleatory noise are optimized
Experiments
43
Network setup and hyperparameters

43. Mean squared error (MSE)
Mean negative log likelihood (MNLL)
Mean Kullback-Leibler (KL) divergence
Experiments
44
Measures for generalization quality

44. Experiments
45
Interpolation

45. Experiments
46
They still don’t extrapolate and they don’t quite realize

46. Experiments
47
Gaussian Process

47. Experiments
Convergence
48

48. Experiments
49
Heteroscedastic noise

49. Experiments
50
Non-Gaussian noise

50. Experiments
51
Uncertainty split
aleatoric epistemic

51. Summary
52
GP MCD DeepE DropoutE QR
Homoscedastic
noise
++ o + o o
Heteroscedastic
noise
-- - ++ + +
Non-Gaussian
noise
+ o + + -
Convergence ++ - + - +
Speed (--) + - / (+) + ++
Uncertainty split yes no yes yes no

52. 1. Motivation
2. Methods
a. Gaussian Processes
b. Monte-Carlo Dropout
c. Deep Ensembles
d. Dropout Ensembles
e. Quantile Regression
3. Experiments
4. Conclusion & Outlook
Agenda
53

53. › Neural network approaches discussed here are very aware of
aleatory uncertainty, however, not capable of correctly estimating
epistemic uncertainty
› Gaussian Processes give clear signals about ignorance but do not
scale
A combined solution needs to be developed because
uncertainty estimation is needed in critical applications
Conclusion
54
There is work to be done

54. › Bayesian Neural Networks (e.g. with PyMC)
› Sparse Gaussian Process approximations
› Gaussian Processes on top of neural networks
Outlook
55
Other approaches

55. Thank You!
Florian Wilhelm
Principal Data Scientist
inovex GmbH
Schanzenstraße 6-20
Kupferhütte 1.13
51063 Köln
florian.wilhelm@inovex.de