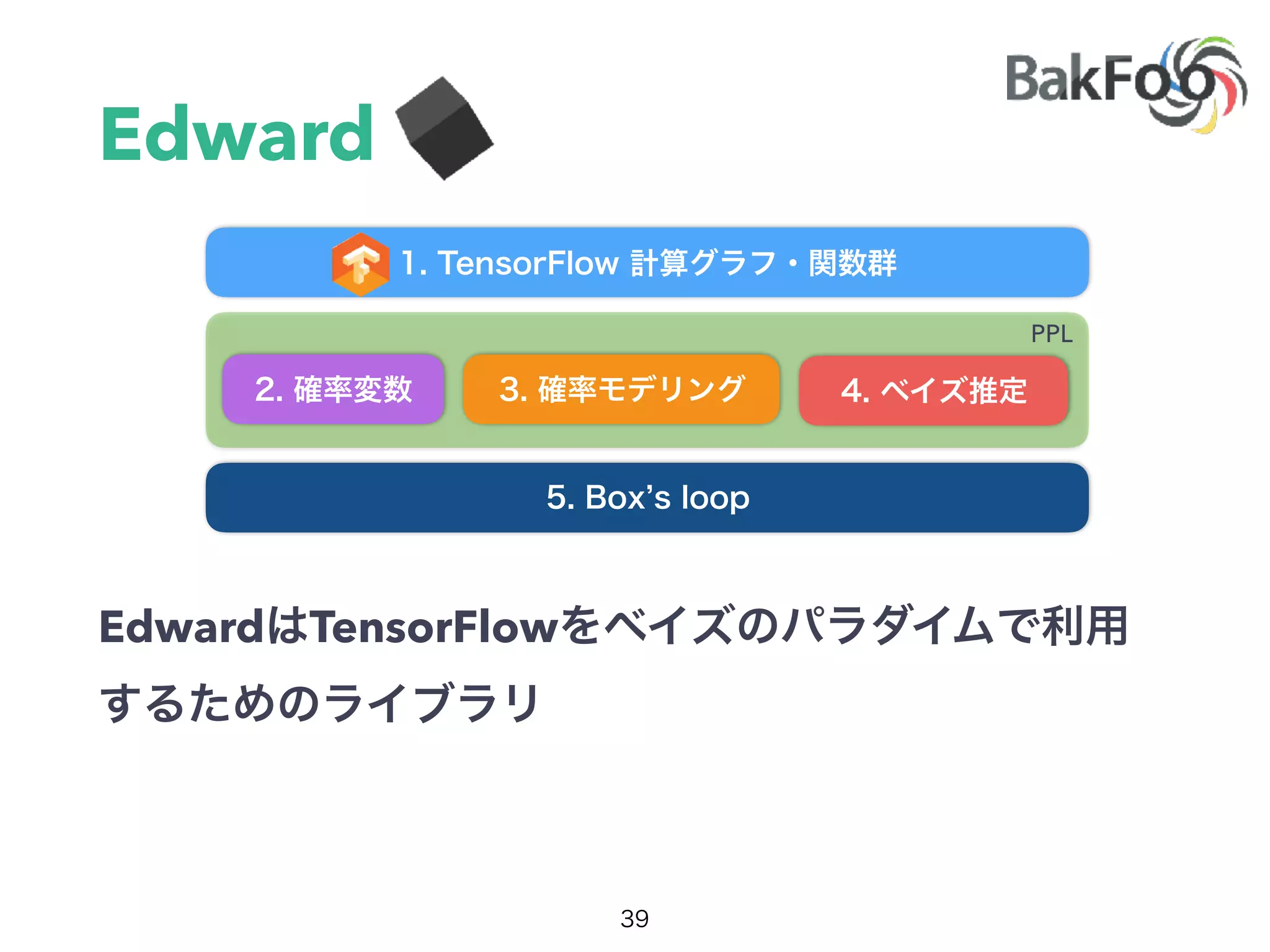
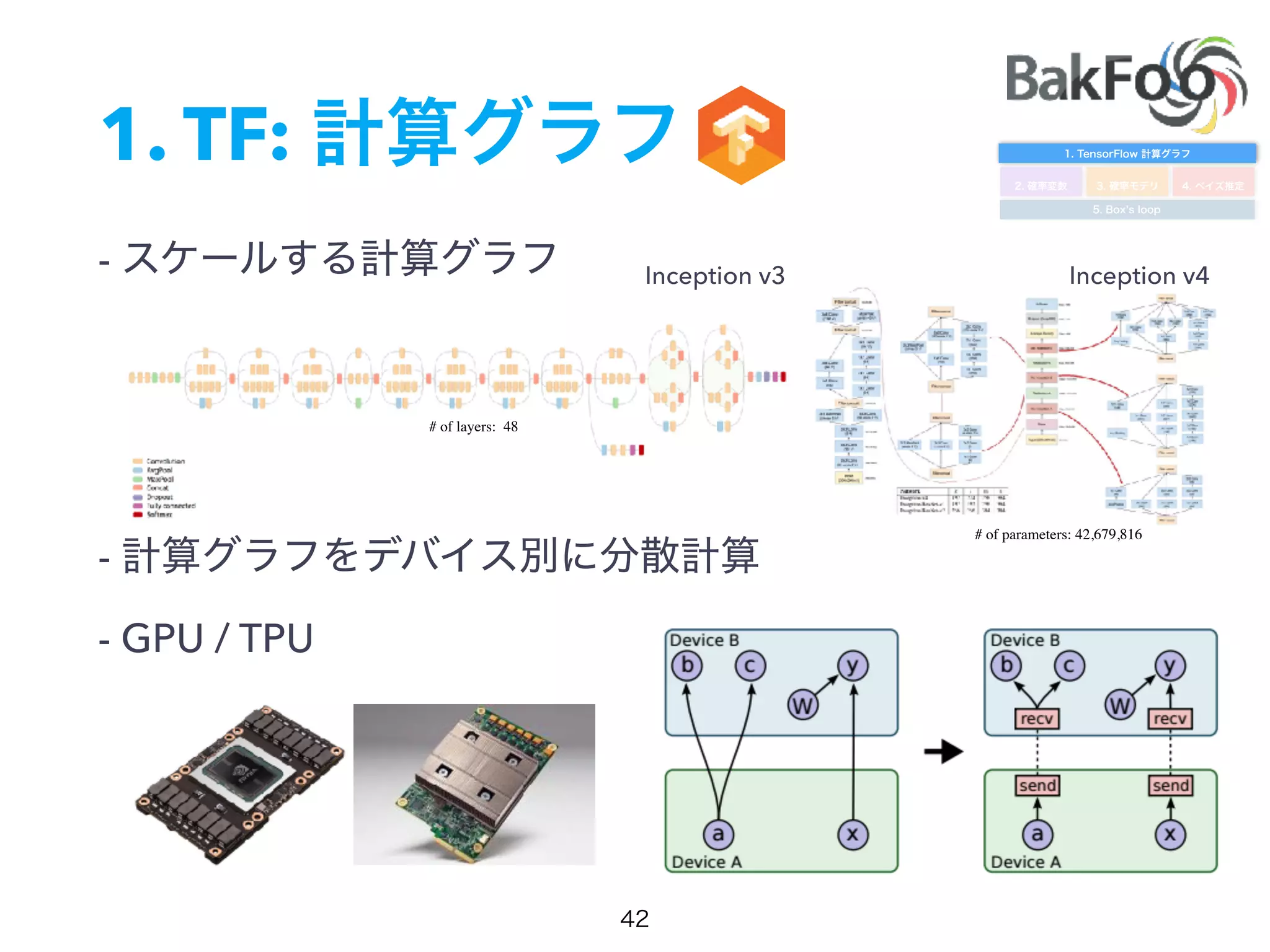
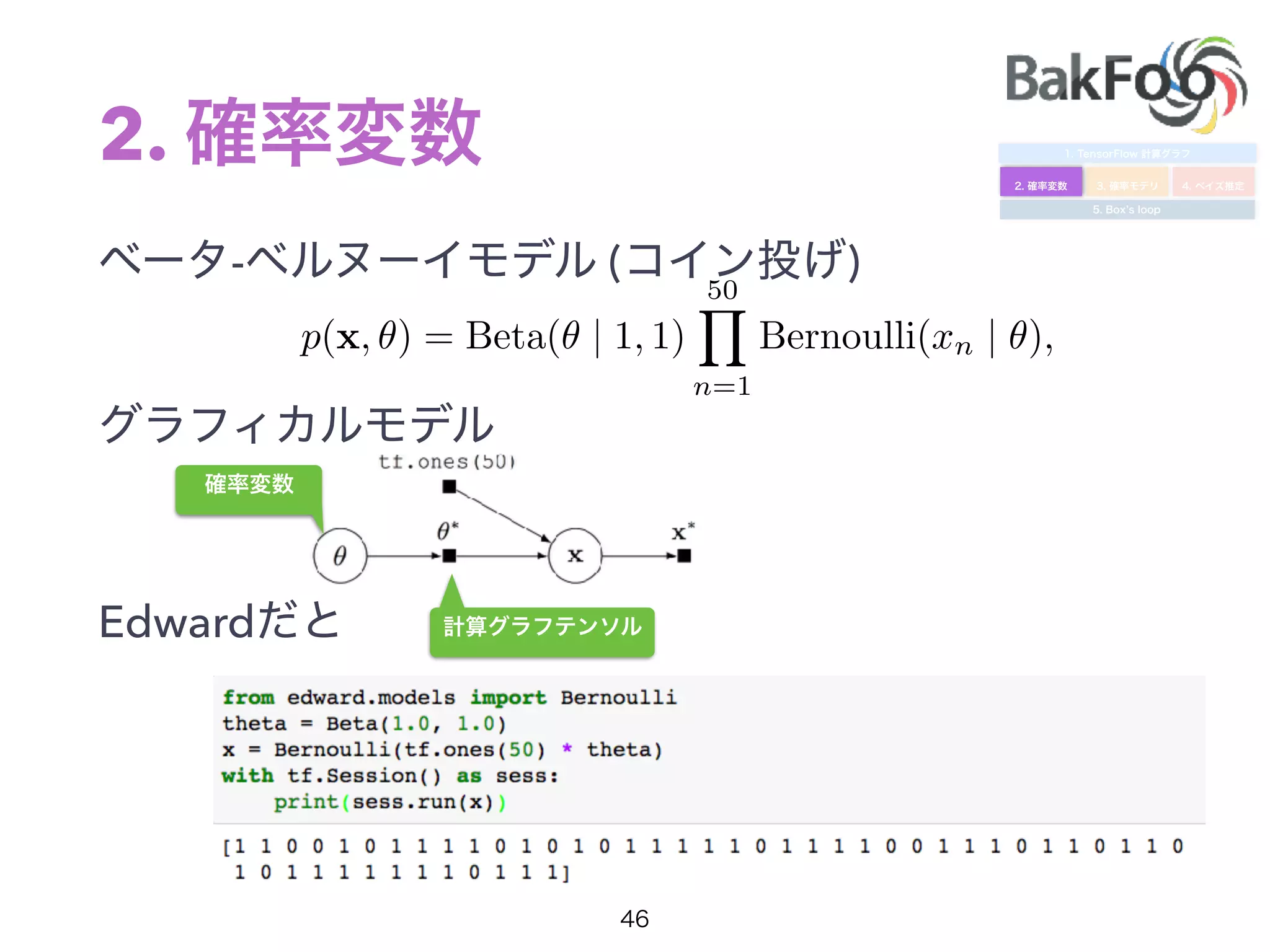
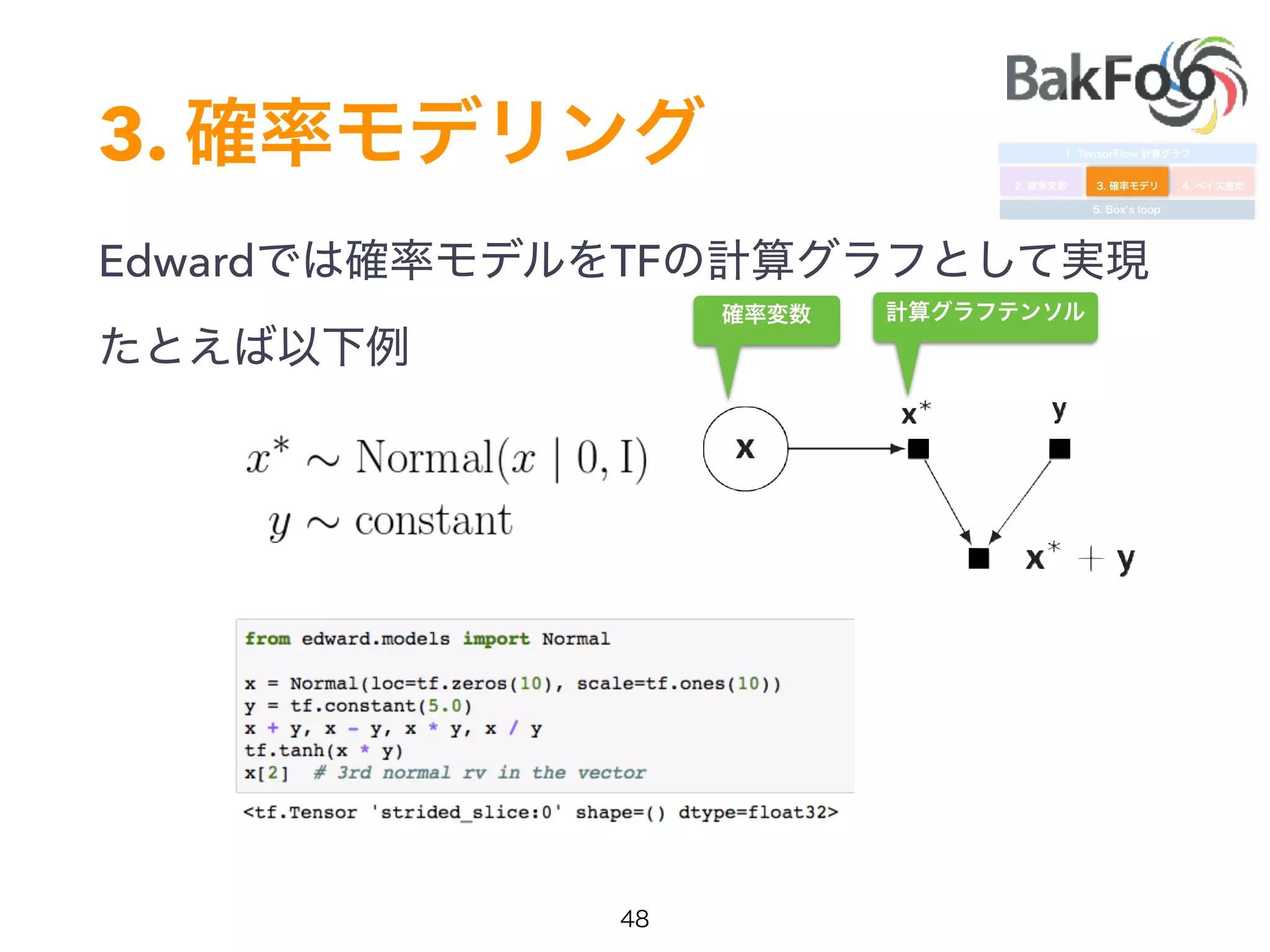
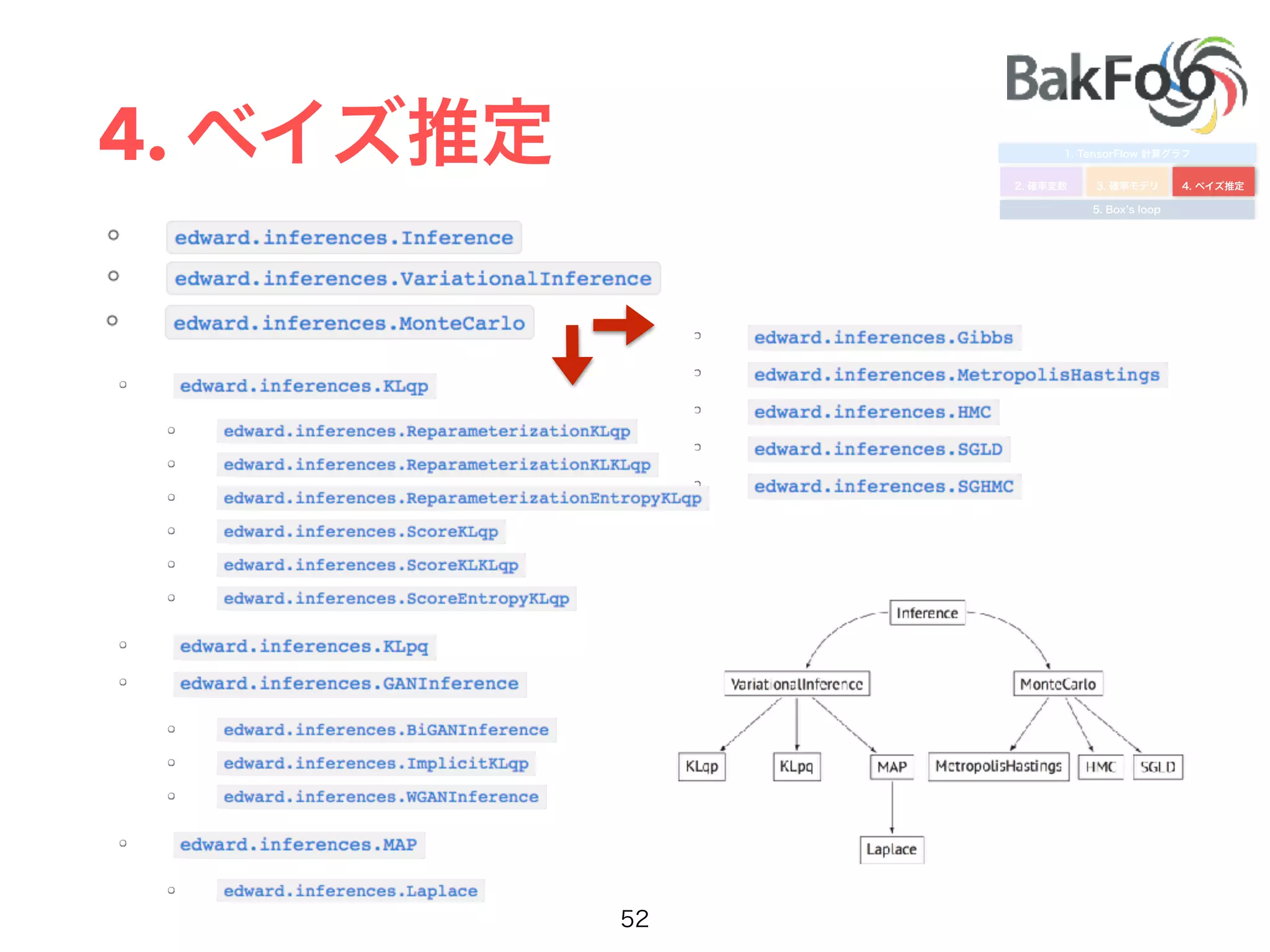
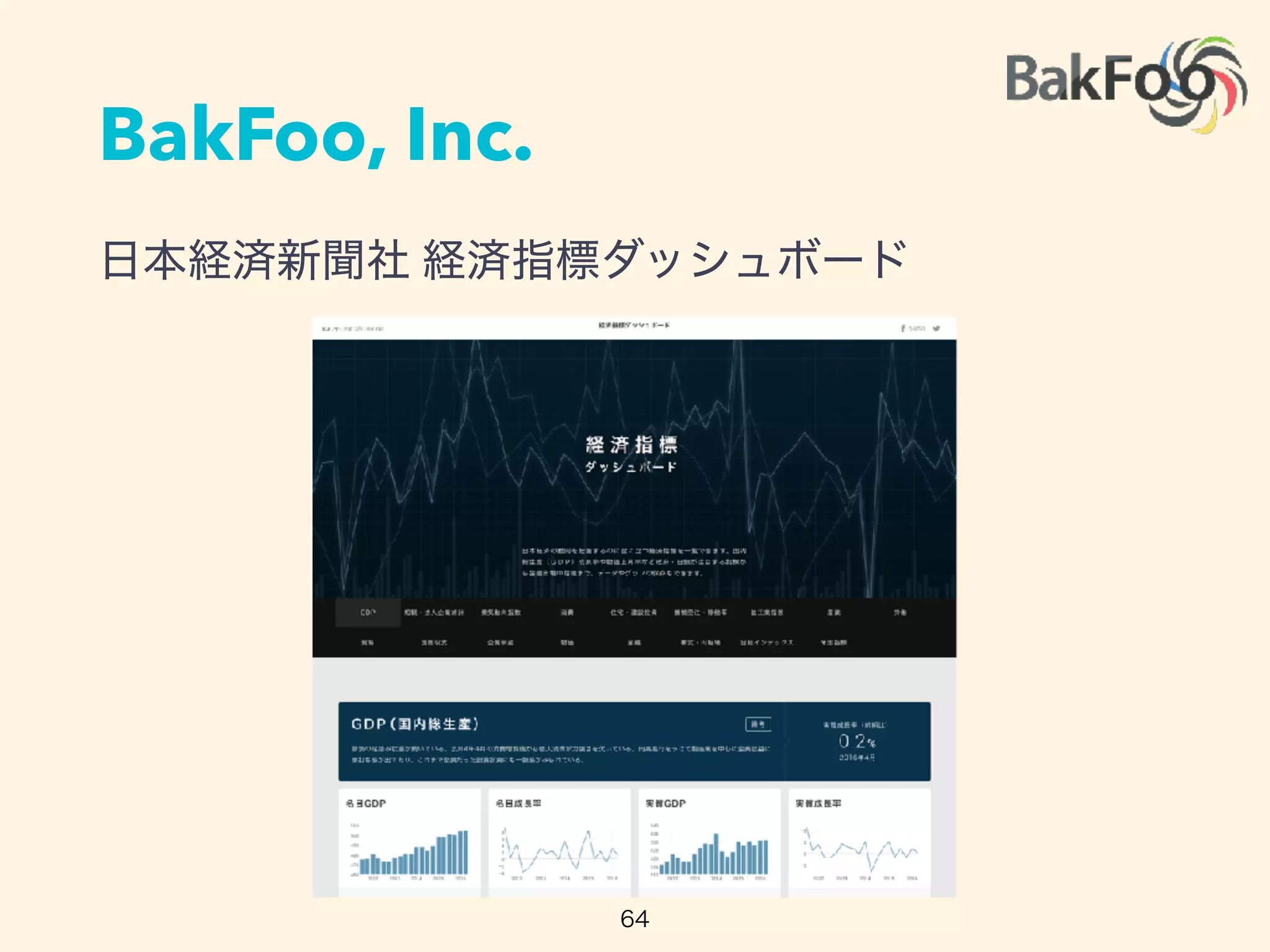
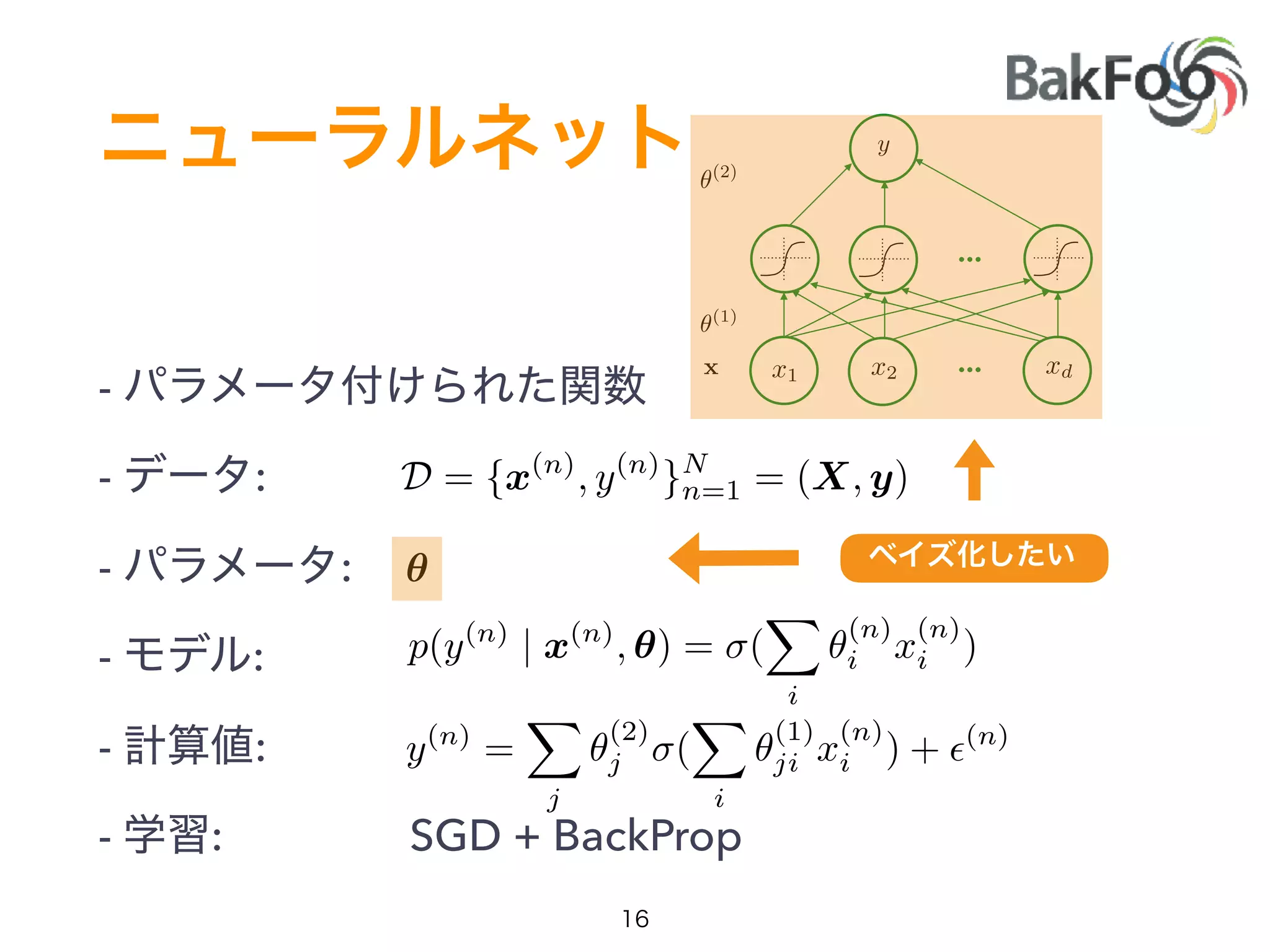
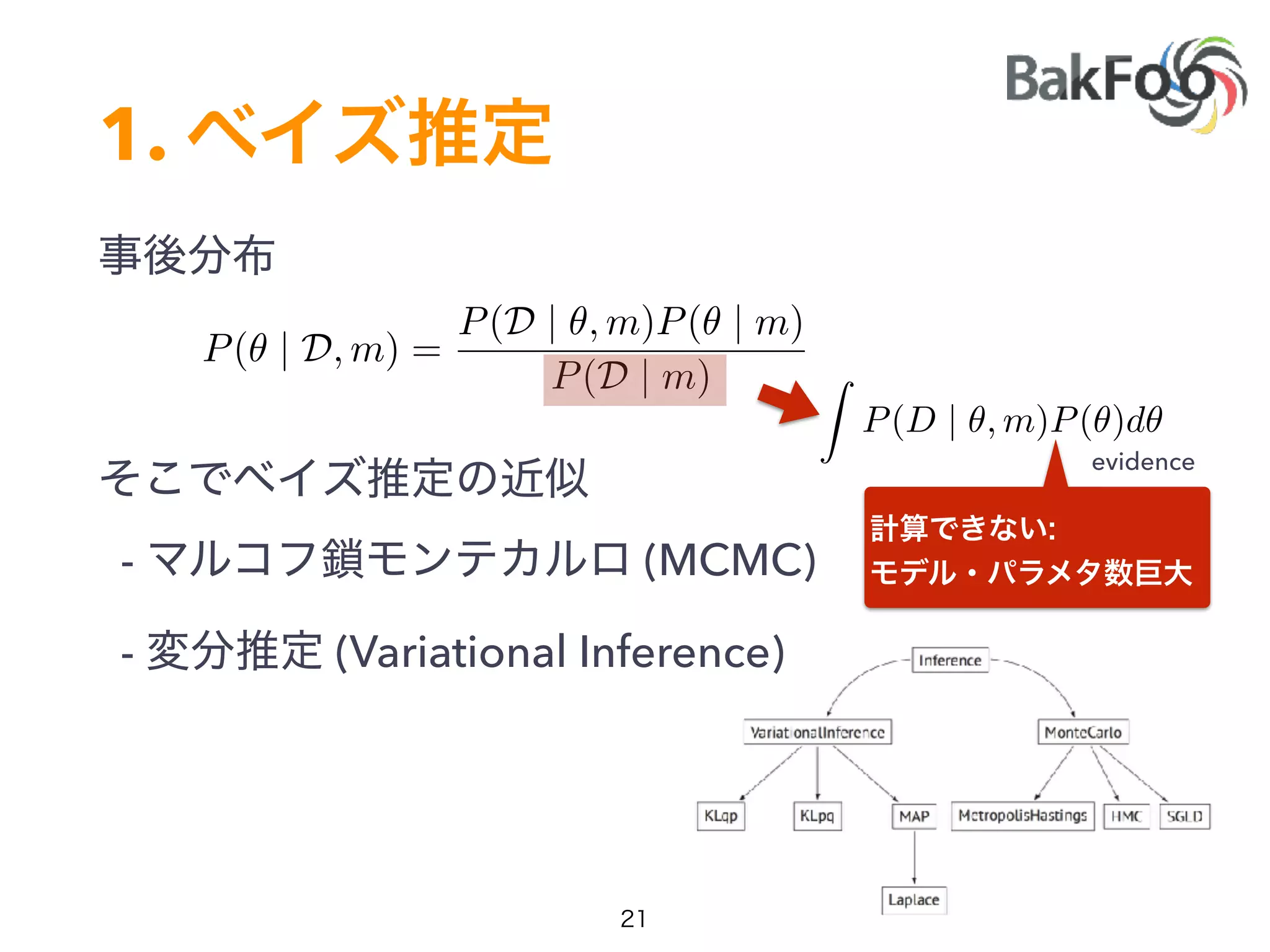
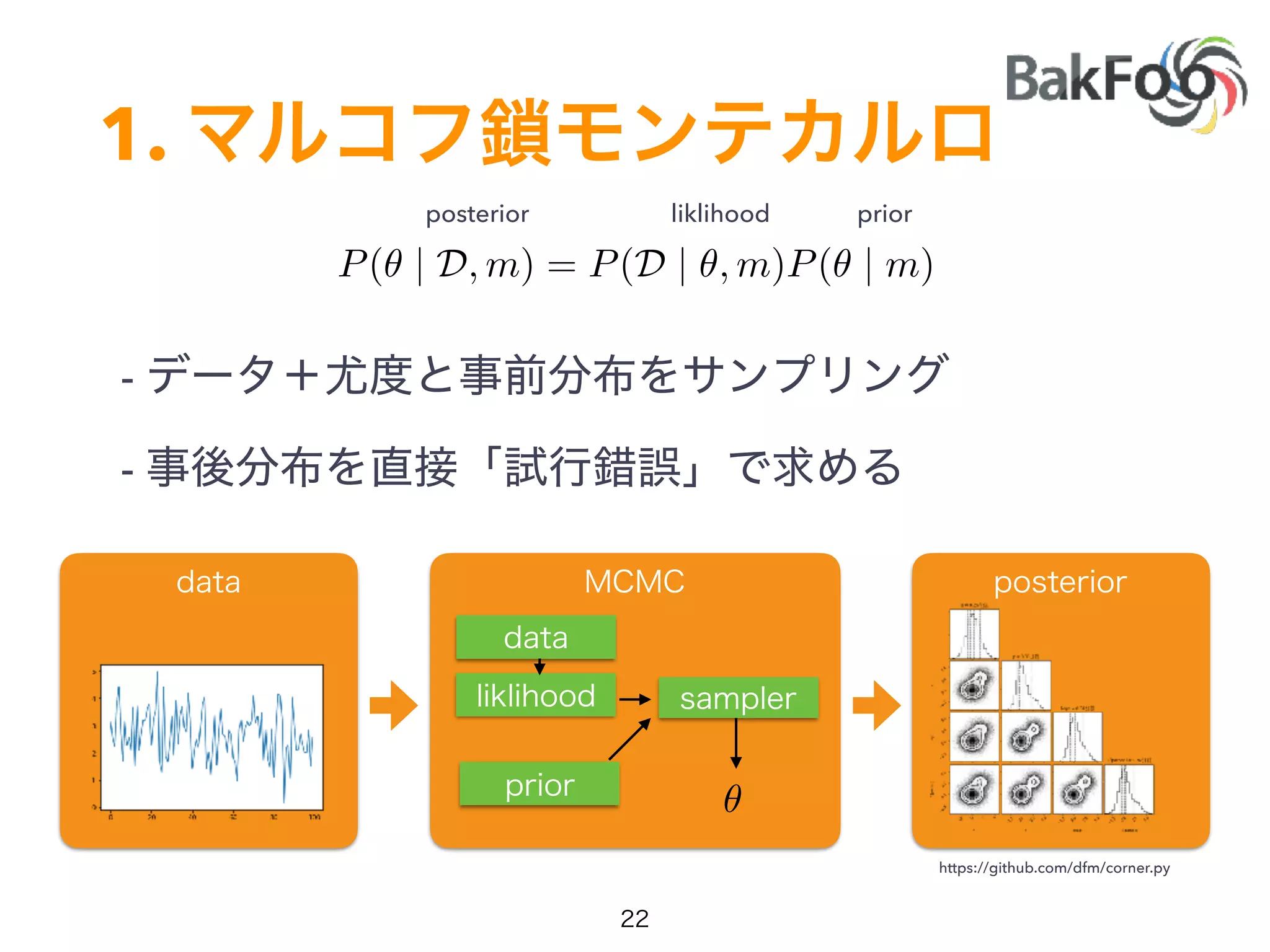
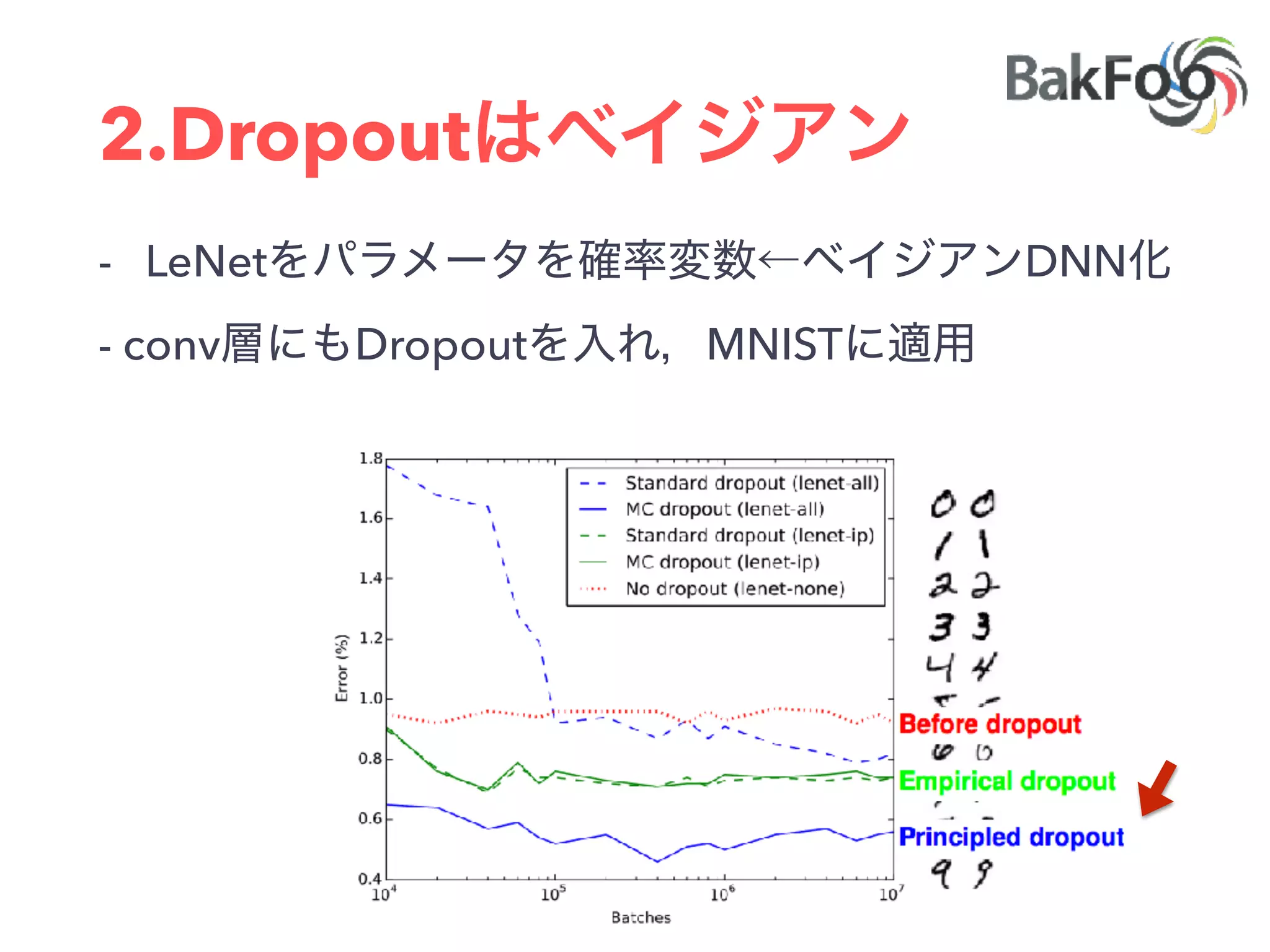
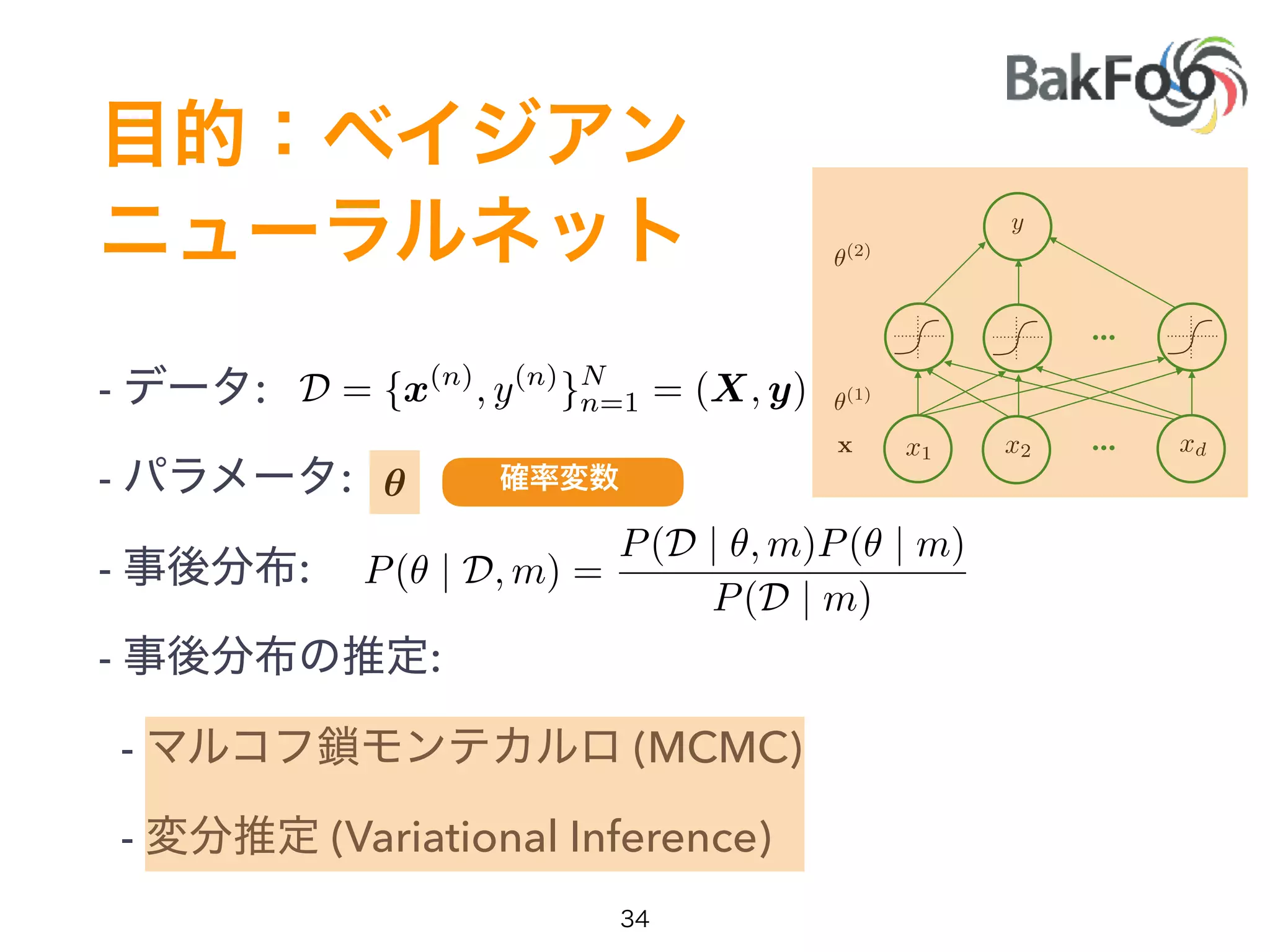
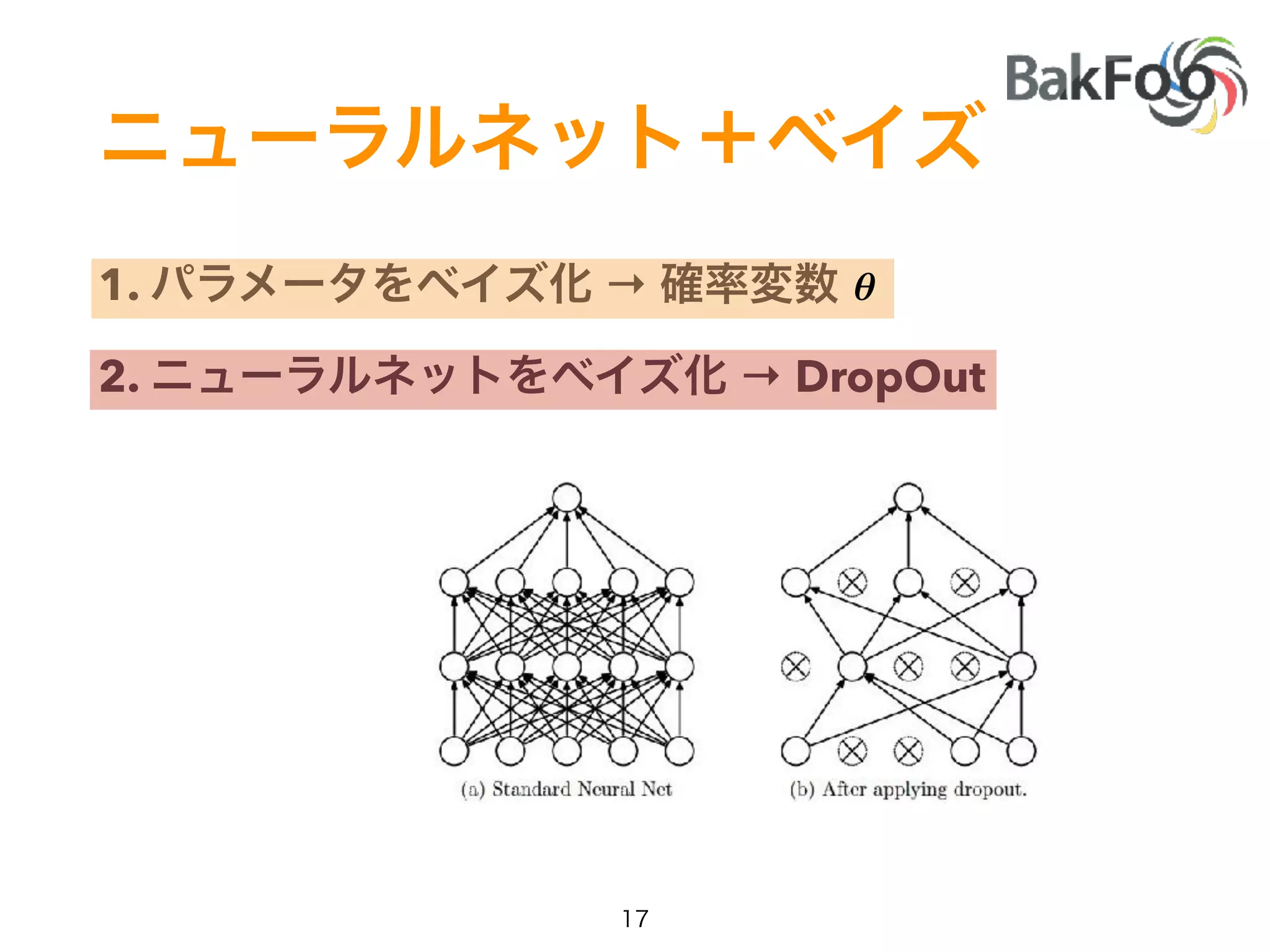
1. Yuta Kashino presented on Edward, a probabilistic programming library built on TensorFlow. Edward allows defining probabilistic models and performing Bayesian inference using techniques like MCMC and variational inference. 2. Dropout was discussed as a way to approximate Bayesian neural networks and model uncertainty in deep learning. Adding dropout to networks can help prevent overfitting. 3. Edward examples were shown using TensorFlow for defining probabilistic models like Bayesian linear regression and hidden Markov models. Models can be easily defined and inference performed.

1. Edward
2017-09-09@ PyConJP 2017

2. Yuta Kashino ( )
BakFoo, Inc. CEO
Astro Physics /Observational Cosmology
Zope / Python
Realtime Data Platform for Enterprise / Prototyping

3. Yuta Kashino ( )
arXiv
PyCon2015
Python
PyCon2016
PyCon2017 DNN PPL Edward
@yutakashino

4. -
- Edward
Edward

6. http://bayesiandeeplearning.org/

7. Shakir Mohamed
http://blog.shakirm.com/wp-content/uploads/2015/11/CSML_BayesDeep.pdf

8. -
Denker, Schwartz, Wittner, Solla, Howard, Jackel, Hopfield (1987)
Denker and LeCun (1991)
MacKay (1992)
Hinton and van Camp (1993)
Neal (1995)
Barber and Bishop (1998)
Graves (2011)
Blundell, Cornebise, Kavukcuoglu, and Wierstra (2015)
Hernandez-Lobato and Adam (2015)

9. -
Yarin Gal
Zoubin Ghahramani
Shakir Mohamed
Dastin Tran
Rajesh Ranganath
David Blei
Ian Goodfellow
Columbia U
U of Cambridge

10. -
- :
- :
- :
- :
- : SGD + BackProp
…
…x1 x2 xd
✓(2)
✓(1)
x
y
y(n)
=
X
j
✓
(2)
j (
X
i
✓
(1)
ji x
(n)
i ) + ✏(n)
p(y(n)
| x(n)
, ✓) = (
X
i
✓
(n)
i x
(n)
i )
✓
D = {x(n)
, y(n)
}N
n=1 = (X, y)

11. :
- +
- 2012 ILSVRC
→ 2015
-
-
-
-

12. :
-
- ReLU, DropOut, Mini Batch, SGD(Adam), LSTM…
-
- ImageNet, MSCoCo…
- : GPU,
- :
- Theano, Torch, Caffe, TensorFlow, Chainer, MxNet, PyTorch…

13. :
-
-
-
-
-
https://lossfunctions.tumblr.com/

14. :
-
-
-
- Adversarial examples
-

15. -
=
=
-

16. -
- :
- :
- :
- :
- : SGD + BackProp
…
…x1 x2 xd
✓(2)
✓(1)
x
y
y(n)
=
X
j
✓
(2)
j (
X
i
✓
(1)
ji x
(n)
i ) + ✏(n)
p(y(n)
| x(n)
, ✓) = (
X
i
✓
(n)
i x
(n)
i )
✓
D = {x(n)
, y(n)
}N
n=1 = (X, y)

17. 1. →
2. → DropOut
✓

18. 1.
- data hypothesis( )
- :
-
-
P(H | D) =
P(H)P(D | H)
P
H P(H)P(D|H)
P(x) =
X
y
P(x, y)
P(x, y) = P(x)P(y | x)
posterior likelihoodprior
evidence

19. 1.
- :
- :
-
-
- :
P(H | D) =
P(H)P(D | H)
P
H P(H)P(D|H)
likelihood priorposterior
P(✓ | D, m) =
P(D | ✓, m)P(✓ | m)
P(D | m)
m:
P(x | D, m) =
Z
P(x | ✓, D, m)P(✓ | D, m)d✓
P(m | D) =
P(D | m)P(m)
P(D)
evidence
✓ ⇠ Beta(✓ | 2, 2)

20. 1.
-
- :
- :
- :
…
…x1 x2 xd
✓(2)
✓(1)
x
y
✓
D = {x(n)
, y(n)
}N
n=1 = (X, y)
P(✓ | D, m) =
P(D | ✓, m)P(✓ | m)
P(D | m)
m:

21. 1.
- (MCMC)
- (Variational Inference)
P(✓ | D, m) =
P(D | ✓, m)P(✓ | m)
P(D | m) Z
P(D | ✓, m)P(✓)d✓
evidence

22. 1.
-
-
P(✓ | D, m) = P(D | ✓, m)P(✓ | m)
liklihood priorposterior
✓
https://github.com/dfm/corner.py

23. 1.
✓
http://twiecki.github.io/blog/2014/01/02/visualizing-mcmc/
NUTS (HMC)
Metropolis
-Hastings

24. 1.

25. P(θ|D,m) KL q(θ)
ELBO
1.
⇤
= argmin KL(q(✓; ) || p(✓ | D))
= argmin Eq(✓; )[logq(✓; ) p(✓ | D)]
ELBO( ) = Eq(✓; )[p(✓, D) logq(✓; )]
⇤
= argmax ELBO( )
P(✓ | D, m) =
P(D | ✓, m)P(✓ | m)
P(D | m)

26. 1.
- KL =ELBO
- P q
q(✓; 1)
q(✓; 5)
p(✓, D) p(✓, D)
✓✓
⇤
= argmax ELBO( )
ELBO( ) = Eq(✓; )[p(✓, D) logq(✓; )]

27. 1.
- P q
- :
- ADVI: Automatic Differentiation Variational Inference
- BBVI: Blackbox Variational Inference
arxiv:1603.00788
arxiv:1401.0118
https://github.com/HIPS/autograd/blob/master/examples/bayesian_neural_net.py

28. 1.
- VI
-
- David MacKay “Lecture 14 of the Cambridge Course”
- PRML 10
http://www.inference.org.uk/itprnn_lectures/

29. 1. Reference
- Zoubin Ghahramani “History of Bayesian neural
networks” NIPS 2016 Workshop Bayesian Deep
Learning
- Yarin Gal “Bayesian Deep Learning"O'Reilly
Artificial Intelligence in New York, 2017

30. 2.
-
- :
- :
- :
- :
- : SGD + BackProp
…
…x1 x2 xd
✓(2)
✓(1)
x
y
y(n)
=
X
j
✓
(2)
j (
X
i
✓
(1)
ji x
(n)
i ) + ✏(n)
p(y(n)
| x(n)
, ✓) = (
X
i
✓
(n)
i x
(n)
i )
✓
D = {x(n)
, y(n)
}N
n=1 = (X, y)
Dropout

31. 2.Dropout
- Yarin Gal ”Uncertainty in Deep Learning”
- Dropout
- Dropout : conv
- LeNet with Dropout
http://mlg.eng.cam.ac.uk/yarin/blog_2248.html

32. 2.Dropout
- LeNet DNN
- conv Dropout MNIST

33. 2.Dropout
- CO2

34. - :
- :
- :
- :
- (MCMC)
- (Variational Inference)
…
…x1 x2 xd
✓(2)
✓(1)
x
y
✓
D = {x(n)
, y(n)
}N
n=1 = (X, y)
P(✓ | D, m) =
P(D | ✓, m)P(✓ | m)
P(D | m)

35. Edward

36. Edward
- Dustin Tran (Open AI)
- Blei Lab
- (PPL)
- 2016 2 PPL
- / TensorFlow
- George Edward Pelham Box
Box-Cox Trans., Box-Jenkins, Ljung-Box test box plot Tukey,
3 2 RA Fisher

37. - Probabilistic Programing Library/Langage
- Stan, PyMC3, Anglican, Church, Venture,Figaro, WebPPL,
Edward
- : Edward / PyMC3
- (VI)
Metropolis Hastings
Hamilton Monte Carlo
Stochastic Gradient Langevin Dynamics
No-U-Turn Sampler
Blackbox Variational Inference
Automatic Differentiation Variational Inference

38. PPL
Edward
TensorFlow(TF) + (PPL)
TF:
PPL: + +

39. PPL
Edward
Edward TensorFlow

40. 1. TF:
-
- :

41. 1. TF:

42. 1. TF:
-
-
- GPU / TPU
Inception v3 Inception v4
# of parameters: 42,679,816
# of layers: 48

43. 1. TF:
- Keras, Slim
- TensorBoard

44. 1. TF:
-
- tf.contrib.distributions

45. 2.
x:
edward
x⇤
s P(x | ↵)
✓⇤
⇠ Beta(✓ | 1, 1)

46. 2.
- ( )
Edward
p(x, ✓) = Beta(✓ | 1, 1)
50Y
n=1
Bernoulli(xn | ✓),

47. 2.
-
log_prob()
-
mean()
-
sample()
- tf.contrib.distributions
51 : https://www.tensorflow.org/api_docs/python/tf/contrib/distributions

48. 3.
Edward TF

49. 3.
Wh Wh
Wx Wx
bh bh
xtxt 1
ht 1 ht
Wy Wy
by by
yt 1 yt
ht = tanh(Whht 1 + Wxxt + bh)
yt ⇠ Normal(Wyht + by, 1).

50. 3.
http://edwardlib.org/tutorials/

51. 4.
- :
- :
- :
- :
- (MCMC)
- (Variational Inference)
…
…x1 x2 xd
✓(2)
✓(1)
x
y
✓
D = {x(n)
, y(n)
}N
n=1 = (X, y)
P(✓ | D, m) =
P(D | ✓, m)P(✓ | m)
P(D | m)

52. 4.

53. Edward MCMC
4. : MCMC

54. Edward : KLqp
4. :

55. 5. Box’s loop
George Edward Pelham Box
Blei 2014

56. 5. Box’s loop

57. Edward
- Edward = TensorFlow +
+ +
- TensorFlow
-
- TF GPU, TPU, TensorBoard, Keras
-
- TensorFlow

59. Refrence
•D. Tran, A. Kucukelbir, A. Dieng, M. Rudolph, D. Liang, and
D.M. Blei. Edward: A library for probabilistic modeling,
inference, and criticism.(arXiv preprint arXiv:1610.09787)
•D. Tran, M.D. Hoffman, R.A. Saurous, E. Brevdo, K. Murphy,
and D.M. Blei. Deep probabilistic programming.(arXiv
preprint arXiv:1701.03757)
•Box, G. E. (1976). Science and statistics. (Journal of the
American Statistical Association, 71(356), 791–799.)
•D.M. Blei. Build, Compute, Critique, Repeat: Data Analysis
with Latent Variable Models. (Annual Review of Statistics
and Its Application Volume 1, 2014)

60. -
- Edward
Edward

61. Questions
kashino@bakfoo.com
@yutakashino

62. BakFoo, Inc.
NHK NMAPS: +

63. BakFoo, Inc.
PyConJP 2015
Python

64. BakFoo, Inc.

65. BakFoo, Inc.
: SNS +

66. 3.
256 28*28