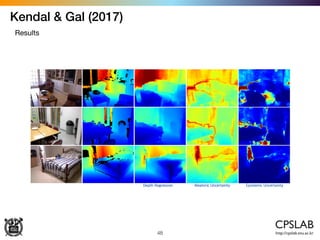
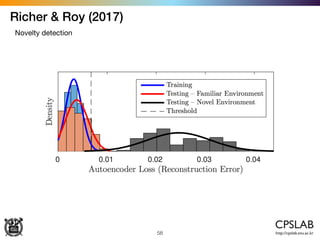
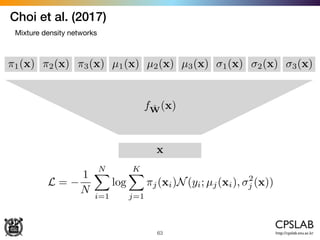
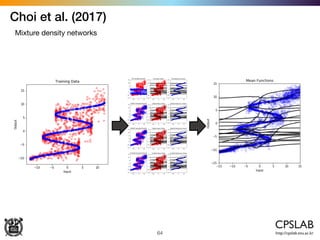
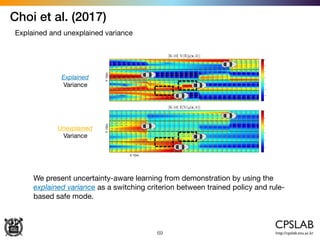
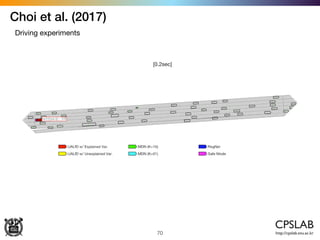
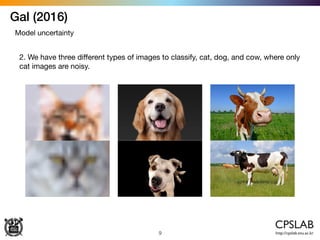
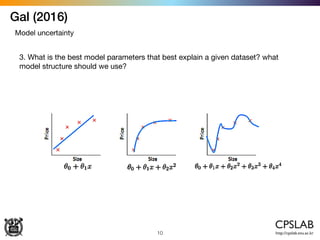
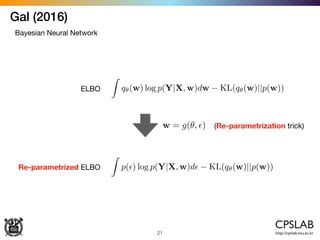
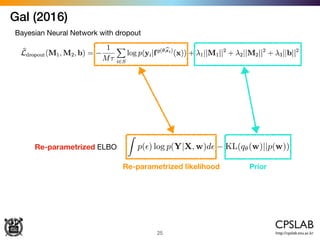
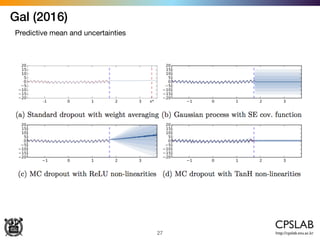
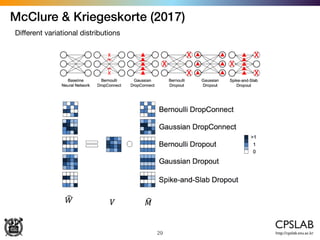
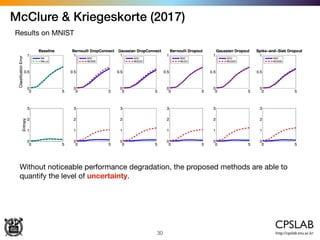
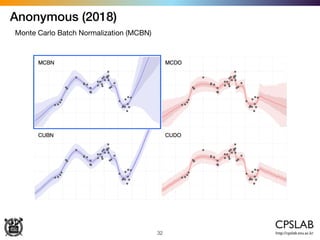
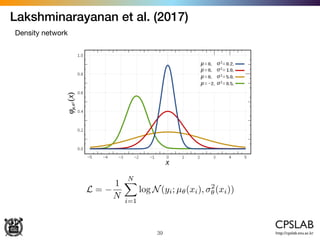
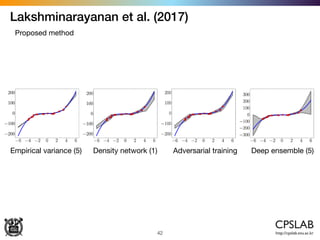
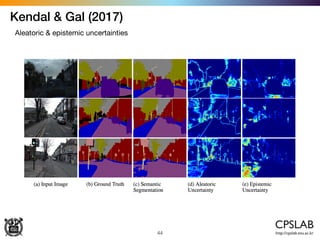
The document discusses the uncertainties in deep learning, highlighting examples of model uncertainty and the application of Bayesian neural networks for managing epistemic and aleatoric uncertainties. It covers various methodologies, including dropout as a Bayesian approximation, variational inference, and the use of mixture density networks to quantify uncertainties in predictive tasks. Additionally, it addresses approaches for safe reinforcement learning and the implications of these uncertainties in practical scenarios.

1. Uncertainties in
Deep Learning
in a nutshell
Sungjoon Choi
CPSLAB, SNU

2. Introduction
2
The first fatality from an assisted driving system

3. Introduction
3
Google Photos identified two black people as 'gorillas'

4. Introduction
4

5. Contents
5

6. Contents
6
Bayesian Neural Network
with variational inference
and re-parametrization trick
Bootstrapping-
based uncertainty
modeling
Bayesian Neural
Network
modeling
epistemic and
aleatoric
uncertainties
Application to
Safe RL
Novelty Detection
using
auto-encoder
Mixture Density
Network modeling
epistemic and
aleatoric
uncertainties

7. 7
Y. Gal, Uncertainty in Deep Learning, 2016

8. Gal (2016)
8
Model uncertainty
1. Given a model trained with several pictures of dog breeds, a user asks the model
to decide on a dog breed using a photo of a cat.

9. Gal (2016)
9
Model uncertainty
2. We have three different types of images to classify, cat, dog, and cow, where only
cat images are noisy.

10. Gal (2016)
10
Model uncertainty
3. What is the best model parameters that best explain a given dataset? what
model structure should we use?

11. Gal (2016)
11
Model uncertainty
1. Given a model trained with several pictures of dog breeds, a user asks the model
to decide on a dog breed using a photo of a cat.
2. We have three different types of images to classify, cat, dog, and cow, where only
cat images are noisy.
3. What is the best model parameters that best explain a given dataset? what
model structure should we use?

12. Gal (2016)
12
Model uncertainty
1. Given a model trained with several pictures of dog breeds, a user asks the model
to decide on a dog breed using a photo of a cat.
2. We have three different types of images to classify, cat, dog, and cow, where only
cat images are noisy.
3. What is the best model parameters that best explain a given dataset? what
model structure should we use?
Out of distribution test data
Aleatoric uncertainty
Epistemic uncertainty

13. Gal (2016)
13
Dropout as a Bayesian approximation
“We show that a neural network with arbitrary depth and non-linearities, with dropout
applied before every weight layer, is mathematically equivalent to an approximation
to a well known Bayesian model.”

14. Gal (2016)
14
Dropout as a Bayesian approximation
The resulting formulations are surprisingly simple.

15. Gal (2016)
15
Bayesian Neural Network
Posterior p(w|X, Y) Prior p(w)
In Bayesian inference, we aim to find a posterior distribution over the random variables of
our interest given a prior distribution which is intractable in many case.

16. Gal (2016)
16
Bayesian Neural Network
p(y⇤
|x⇤
, X, Y) =
Z
p(y⇤
|x⇤
, w)p(w|X, Y)dw
Posterior p(w|X, Y)
Inference
Prior p(w)
Note that even when given a posterior distribution, exact inference is very likely to be
intractable as it contains integral with respect to the distribution over latent variables.

17. Gal (2016)
17
Bayesian Neural Network
p(y⇤
|x⇤
, X, Y) =
Z
p(y⇤
|x⇤
, w)p(w|X, Y)dw
Posterior p(w|X, Y)
Inference
Variational Inference KL (q✓(w)||p(w|X, Y)) =
Z
q✓(w) log
q✓(w)
p(w|X, Y)
dw
Prior p(w)
Variational inference is used to approximate the (intractable) posterior distribution
with (tractable) variational distribution with respect to the KL divergence.

18. Gal (2016)
18
Bayesian Neural Network
p(y⇤
|x⇤
, X, Y) =
Z
p(y⇤
|x⇤
, w)p(w|X, Y)dw
Posterior p(w|X, Y)
Inference
Variational Inference KL (q✓(w)||p(w|X, Y)) =
Z
q✓(w) log
q✓(w)
p(w|X, Y)
dw
ELBO
Z
q✓(w) log p(Y|X, w)dw KL(q✓(w)||p(w))
Prior p(w)
Minimizing the KL divergence is equivalent to maximizing the evidence lower bound
(ELBO) which also contains the integral with respect to the distribution over latent
variables.

19. Gal (2016)
19
Bayesian Neural Network
p(y⇤
|x⇤
, X, Y) =
Z
p(y⇤
|x⇤
, w)p(w|X, Y)dw
Posterior p(w|X, Y)
Inference
Variational Inference KL (q✓(w)||p(w|X, Y)) =
Z
q✓(w) log
q✓(w)
p(w|X, Y)
dw
ELBO
Z
q✓(w) log p(Y|X, w)dw KL(q✓(w)||p(w))
Prior p(w)
Instead of the posterior distribution, we only need a likelihood to compute the ELBO.

20. Gal (2016)
20
Bayesian Neural Network
p(y⇤
|x⇤
, X, Y) =
Z
p(y⇤
|x⇤
, w)p(w|X, Y)dw
Posterior p(w|X, Y)
Inference
Variational Inference KL (q✓(w)||p(w|X, Y)) =
Z
q✓(w) log
q✓(w)
p(w|X, Y)
dw
ELBO
Z
q✓(w) log p(Y|X, w)dw KL(q✓(w)||p(w))
ELBO (reparametrization)
Z
p(✏) log p(Y|X, w)d✏ KL(q✓(w)||p(w))
w = g(✓, ✏)
Prior p(w)

21. Gal (2016)
21
Bayesian Neural Network
ELBO
Z
q✓(w) log p(Y|X, w)dw KL(q✓(w)||p(w))
Re-parametrized ELBO
Z
p(✏) log p(Y|X, w)d✏ KL(q✓(w)||p(w))
w = g(✓, ✏) (Re-parametrization trick)

22. Gal (2016)
22
Gaussian process approximation
MC approximation
Apply to Gaussian processes
GP Marginal likelihood

23. Gal (2016)
23
Bayesian Neural Network with dropout

24. Gal (2016)
24
Bayesian Neural Network with dropout
p(y|fg(✓,ˆ✏)
(x)) = N(y; ˆy✓(x), ⌧ 1
ID)
Likelihood

25. Gal (2016)
25
Bayesian Neural Network with dropout
Re-parametrized ELBO
Z
p(✏) log p(Y|X, w)d✏ KL(q✓(w)||p(w))
Re-parametrized likelihood Prior

26. Gal (2016)
26
Bayesian Neural Network with dropout

27. Gal (2016)
27
Predictive mean and uncertainties

28. 28
P. McClure, Representing Inferential Uncertainty in Deep
Neural Networks Through Sampling, 2017

29. McClure & Kriegeskorte (2017)
29
Different variational distributions

30. McClure & Kriegeskorte (2017)
30
Results on MNIST
Without noticeable performance degradation, the proposed methods are able to
quantify the level of uncertainty.

31. 31
Anonymous, Bayesian Uncertainty Estimation for
Batch Normalized Deep Networks, 2018

32. Anonymous (2018)
32
Monte Carlo Batch Normalization (MCBN)

33. Anonymous (2018)
33
Batch normalized deep nets as Bayesian modeling
Learnable parameter
Stochastic parameter

34. Anonymous (2018)
34
Batch normalized deep nets as Bayesian modeling

35. Anonymous (2018)
35
MCBN to Bayesian SegNet

36. 36
B. Lakshminarayanan et al., Simple and Scalable Predictive Uncertainty
Estimation using Deep Ensembles, 2017

37. Lakshminarayanan et al. (2017)
37
Proper scoring rule
“A scoring rule assigns a numerical score to a predictive distribution
rewarding better calibrated predictions over worse. (…) It turns out many
common neural network loss functions are proper scoring rules.”

38. Lakshminarayanan et al. (2017)
38
Density network
x
µ✓(x) ✓(x)
L =
1
N
NX
i=1
log N(yi; µ✓(xi), 2
✓(xi))
f✓(x)

39. Lakshminarayanan et al. (2017)
39
Density network
L =
1
N
NX
i=1
log N(yi; µ✓(xi), 2
✓(xi))

40. Lakshminarayanan et al. (2017)
40
Adversarial training with a fast gradient sign method
“Adversarial training can be also be interpreted as a computationally
efficient solution to smooth the predictive distributions by increasing the
likelihood of the target around an neighborhood of the observed training
examples.”

41. Lakshminarayanan et al. (2017)
41
Proposed method
Train M different models

42. Lakshminarayanan et al. (2017)
42
Proposed method
Empirical variance (5) Density network (1) Adversarial training Deep ensemble (5)

43. 43
A. Kendal and Y. Gal, What Uncertainties Do We Need in
Bayesian Deep Learning for Computer Vision?, 2017

44. Kendal & Gal (2017)
44
Aleatoric & epistemic uncertainties

45. Kendal & Gal (2017)
45
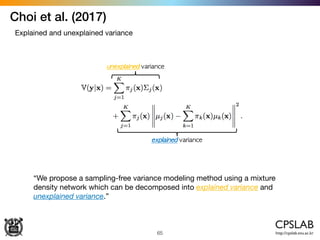
Aleatoric & epistemic uncertainties
ˆW ⇠ q(W)
x
ˆy ˆW(x) ˆ2
ˆW
(x)
[ˆy, ˆ2
] = f
ˆW
(x)
L =
1
N
NX
i=1
log N(yi; ˆy ˆW(x), ˆ2
ˆW
(x))

46. Kendal & Gal (2017)
46
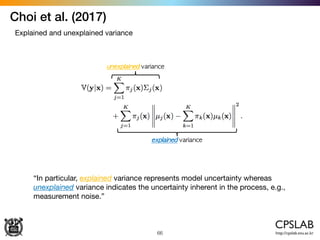
Heteroscedastic uncertainty as loss attenuation
ˆW ⇠ q(W)
x
ˆy ˆW(x) ˆ2
ˆW
(x)
[ˆy, ˆ2
] = f
ˆW
(x)

47. Kendal & Gal (2017)
47
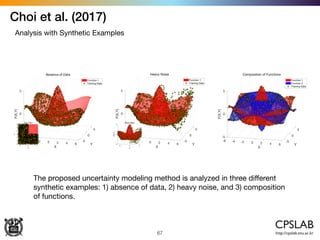
Aleatoric & epistemic uncertainties
ˆW ⇠ q(W)
x
ˆy ˆW(x) ˆ2
ˆW
(x)
[ˆy, ˆ2
] = f
ˆW
(x)
Var(y) ⇡
1
T
TX
t=1
ˆy2
t
TX
t=1
ˆyt
!2
+
1
T
TX
t=1
ˆ2
t
Epistemic unct. Aleatoric unct,

48. Kendal & Gal (2017)
48
Results

49. 49
G. Khan et al., Uncertainty-Aware Reinforcement
Learning from Collision Avoidance, 2016

50. Khan et al. (2016)
50
Uncertainty-Aware Reinforcement Learning
Uncertainty-aware collision prediction model

51. Khan et al. (2016)
51
Uncertainty-Aware Reinforcement Learning
“Uncertainty is based on bootstrapped neural networks using dropout.”
Bootstrapping?
- Generate multiple datasets using sampling with replacement.
- The intuition behind bootstrapping is that, by generating multiple populations
and training one model per population, the models will agree in high-density
areas (low uncertainty) and disagree in low-density areas (high uncertainty).
Dropout?
- “Dropout can be viewed as an economical approximation of an ensemble
method (such as bootstrapping) in which each sampled dropout mask
corresponds to a different model.”

52. Khan et al. (2016)
52
Uncertainty-Aware Reinforcement Learning
Train B different models

53. 53

54. Richer & Roy (2017)
54
Introduction
State-of-the-art deep learning methods are known to produce erratic or unsafe
predictions when faced with novel inputs. Furthermore, recent ensemble, bootstrap
and dropout methods for quantifying neural network uncertainty may not efficiently
provide accurate uncertainty estimates when queried with inputs that are very different
from their training data.
We use a conventional feedforward neural network to predict collisions based on
images observed by the robot, and we use an autoencoder to judge whether those
images are similar enough to the training data for the resulting neural network
predictions to be trusted.

55. Richer & Roy (2017)
55
Novelty detection
Use the reconstruction error as a measure of novelty.

56. Richer & Roy (2017)
56
Novelty detection
Use the reconstruction error as a measure of novelty.

57. Richer & Roy (2017)
57
Novelty detection

58. Richer & Roy (2017)
58
Novelty detection

59. Richer & Roy (2017)
59
Learning to predict collision
c
ˆmt
it
at
fc(c|it, at)
fp(c| ˆmt, at)
fn(it)
where
: collision
: estimated map
: input image
: action
: neural net trained to predict collision
: prior estimate of collision probability
: novelty detection

60. Richer & Roy (2017)
60
Experiments
“Using an autoencoder as a measure of uncertainty in our collision prediction
network, we can transition intelligently between the high performance of the learned
model and the safe, conservative performance of a simple prior, depending on
whether the system has been trained on the relevant data.”

61. Richer & Roy (2017)
61
Experiments
“In the hallway training environment, we achieved a mean speed of 3.26 m/s and a top
speed over 5.03 m/s. This result significantly exceeds the maximum speeds achieved
when driving in this environment under the prior estimate of collision probability before
performing any learning.”
“On the other hand, in the novel environment, for which our model was untrained, the
novelty detector correctly identified every image as being unfamiliar. In the novel
environment, we achieved a mean speed of 2.49 m/s and a maximum speed of 3.17 m/s.”

62. 62
S. Choi et al., Uncertainty-Aware Learning from Demonstration Using
Mixture Density Networks with Sampling-Free Variance Modeling, 2017
All in this room!

63. Choi et al. (2017)
63
Mixture density networks
x
µ1(x) µ2(x) µ3(x)⇡1(x) ⇡2(x) ⇡3(x) 1(x) 2(x) 3(x)
f ˆW(x)
L =
1
N
NX
i=1
log
KX
j=1
⇡j(xi)N(yi; µj(xi), 2
j (x))

64. 64
Choi et al. (2017)
Mixture density networks

65. 65
Choi et al. (2017)
Explained and unexplained variance
“We propose a sampling-free variance modeling method using a mixture
density network which can be decomposed into explained variance and
unexplained variance.”

66. 66
Choi et al. (2017)
Explained and unexplained variance
“In particular, explained variance represents model uncertainty whereas
unexplained variance indicates the uncertainty inherent in the process, e.g.,
measurement noise.”

67. 67
Choi et al. (2017)
Analysis with Synthetic Examples
The proposed uncertainty modeling method is analyzed in three different
synthetic examples: 1) absence of data, 2) heavy noise, and 3) composition
of functions.

68. 68
Choi et al. (2017)
Analysis with Synthetic Examples

69. 69
Choi et al. (2017)
Explained and unexplained variance
We present uncertainty-aware learning from demonstration by using the
explained variance as a switching criterion between trained policy and rule-
based safe mode.
Unexplained
Variance
Explained
Variance

70. 70
Choi et al. (2017)
Driving experiments

71. 71
)
( . )