Download to read offline
![[PRML] パターン認識と機械学習（第2章：確率分布）](https://cdn.slidesharecdn.com/ss_thumbnails/prmlchapter2-171002030018-thumbnail.jpg?width=640&height=640&fit=bounds)
![[DL輪読会]EfficientNet: Rethinking Model Scaling for Convolutional Neural Networks](https://cdn.slidesharecdn.com/ss_thumbnails/yokota20190621dlhack-190621022108-thumbnail.jpg?width=640&height=640&fit=bounds)
PRML 5.5.6-5.6 畳み込みネットワーク（CNN）・ソフト重み共有・混合密度ネットワーク
- 1.
- 2. 目次 ・5.5 ニューラルネットの正則化 ・5.5.6 畳み込みネットワーク（P270～272） ・5.5.7ソフト重み共有（P272～274） ・5.6 混合密度ネットワーク（P274～280）
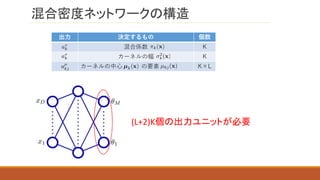
- 3. アブストラクト 5.5.6 入力の変換（平行移動, 回転など）に対して, 出力が不変であるためのアプローチの 一つである,たたみ込みニューラルネットワーク（ＣＮＮ）を紹介する. ＣＮＮは入力に対 して, フィルタによるたたみ込み, 一部の数値を取り出す, といった処理を行うことで特 徴を抽出し, 結果を出力する手法である. 5.5.7 ネットワークの有効な複雑さを削減するために, ソフト重み共有という正則化項を導入 する. ソフト重み共有では, 重みに対して混合分布を導入し, 平均や分散などのパラ メータをグループ毎に学習する. この際, 一つの分布の平均を0にし, 不要な重みを見 つけ出す. これをカットすることでネットワークを軽量化する. 5.6 多峰性を持つ問題に対応するために, データの分布として, 混合分布を仮定する, 混合密度ネットワークについて紹介する.
- 4.
- 5.
- 6.
- 7.
- 8. たたみ込み演算による特徴抽出 入力画像の画素表記 (簡略のため２値) フィルタ(重み) (簡略のためバイアス０を想定) 0 1 1 11 0 1 0 0 0 1 1 0 0 1 1 1 1 0 1 0 0 入力画像 × 0 1 1 0 たたみ込み演算：画像の値とフィルタの値を要素ごとに掛け合 わせ, それらの値を合計する 2 フィルタ 特徴マップ （たたみ込み層の入力）
- 9. たたみ込み演算による特徴抽出 0 1 1 11 0 1 0 0 入力画像 × 0 1 1 0 2 2 フィルタ 特徴マップ （たたみ込み層の入力）
- 10. たたみ込み演算による特徴抽出 0 1 1 11 0 1 0 0 入力画像 × 0 1 1 0 2 2 2 フィルタ 特徴マップ （たたみ込み層の入力）
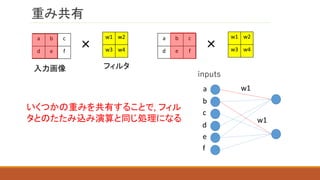
- 11. たたみ込み演算による特徴抽出 0 1 1 11 0 1 0 0 入力画像 × 0 1 1 0 2 2 2 0 フィルタ この値を活性化関数で変 換したものが, たたみ込み 層の出力となる 特徴マップ （たたみ込み層の入力）
- 12. 平行移動と歪みに対しての不変性 0 1 1 11 0 1 0 0 入力画像 × 0 1 1 0 2 2 2 0 フィルタ 特徴マップ 0 0 0 1 1 1 1 1 0 入力画像を平行 移動したもの × 0 1 1 0 2 1 2 2 フィルタ 特徴マップ の部分を全て １マス下に移動 特徴マップの該当部 分も１マス下に移動 ⇒平行移動と歪みに 対しての不変性
- 13. 複数の特徴を抽出する場合 0 1 1 11 0 1 0 0 0 1 1 0 0 1 1 1 1 0 1 0 0 入力画像 × 0 1 1 0 2 2 2 0 フィルタ1 別の特徴を抽出するためには別のフィルタを利用する 0 0 1 1 0 1 1 1 1 0 1 0 0 入力画像 × 2 1 1 0 フィルタ2 0 0 1 1 入力画像 フィルタ2フィルタ1 特徴マップ2 （たたみ込み層の入力） 特徴マップ1 （たたみ込み層の入力）
- 14.
- 15.
- 16. ＣＮＮの３つの機構 ・部分サンプリング - 一部の特徴のみを抽出する. ・局所的受容野 - それぞれのユニットが一部の入力の影響しか受けない. ・重み共有 -特徴を抽出するための重みは同じものを使う. ⇒この二つの機構により, たたみ込み演算と同様の処理が行われる
- 17.
- 18.
- 19. 局所的受容野 入力画像 × w1 w2 w3 w4 フィルタ ab c d e f inputs a b c d e f w1 w2 w3 w4 C, f からは影響を受けない 簡略化のためバイアスは省略
- 20.
- 21. 重み共有 入力画像 × w1 w2 w3 w4 フィルタ ab c d e f × w1 w2 w3 w4 a b c d e f inputs a b c d e f w1 w1 いくつかの重みを共有することで, フィル タとのたたみ込み演算と同じ処理になる
- 22.
- 23.
- 24.
- 25. 3.57 6.7 7.3 16.4 11.7 25.8 28.2 ILSVRC'15 ILSVRC'14ILSVRC'14 ILSVRC'13 ILSVRC'12 ILSVRC'11 ILSVRC'10 ResNet GoogleNet VGG AlexNet ImageNet Classification top-5 error (%) shallow8 layers 19 layers22 layers 152 layers 8 layers 層の増加の歴史
- 26.
- 27. ResNet ・現在の画像認識ではこの仕組みを応用したモデルが広く用いられ ている. ・求める写像を とし, その写像と入力の差分をネットワー クに学習させる仕組み. ショートカットして与えた入力と差分を足して, 出力とする. 入力のショートカット
- 28.
- 29.
- 30. 実際の構造 特徴マップを増やす場所では, 比較の際, 入力の特徴マッ プを増やす操作（パディング）が行われる. ⇒増加分を全て0にする,同じ数の1×1フィルタを使用する.
- 31.
- 32.
- 33. ネットワークの複雑さを軽減する 重み共有の制限を緩め れば, 制限の形がわから くても良くなるのでは？ w1w2 w3 w4 一部の重みが似た値を取りやすくする ⇒ソフト重み共有
- 34. ソフト重み共有 ・誤差関数に正則化項を導入し, 重みをグループ分けし, 同じグループに属す る重みが似たような値を取りやすくする. ・重みのグループ分け,グループの平均などのパラメータが学習過程の一部 として決定される（自分であらかじめ決めるが, データによって修正される）. inputs a b c d e f w1 w2 𝑤1, 𝑤2 ∈ A w1とw2が似た値を取る
- 35. ソフト重み共有がネットワークを圧縮する仕組み ・一つのグループの平均に0を決めておき, そのグループを取る可能性が高 いように事前のパラメータを設定すると, いくつかの不要な重みが見つかる. ・尤度（データの起こりやすさ）の計算を行うことで,精度をあまり落とさずに 圧縮されたネットワークを見つけることが出来る. inputs a b c d e f w1 w2 𝑤1, 𝑤2 ∈ A A：平均が0の重 みのグループ inputs a b c d e f Aに属する重 みを捨てる 圧縮されたネットワーク
- 36.
- 37.
- 38.
- 39. ネットワークの誤差関数 これを最小化するように, 重み, グループ毎の平均,グ ループ毎の分散を決める. 重みとパラメータは依存しあっているので, 同時最適化 が望ましく, 共役勾配法や準ニュートン法が用いられる. 忘れた人は最適化数学の本参照
- 40.
- 41.
- 42.
- 43.
- 44.
- 45.
- 46. 教師有り学習の目標 これまでの仮定（多項式曲線フィッティングの例） ガウス分布は単峰性を持つため, 多峰性を持つ問題に対応できない. 単峰性 多峰性 目標：がどんな分布か知りたい（平均などのパラメータも含めて） 多峰性：極大値 が複数あること
- 47.
- 48. 多峰性を持つ人工的なデータの学習 二乗和誤差関数を用いた二層ニューラルネットで学習 : 一様分布 に従う確率変数𝑥からサンプリングしたもの :関数 に から生成される乱数を加えたもの
- 49.
- 50. 多峰性の確認 0 1 多峰性 𝑥1 𝑥1 𝑥2 𝑥2 t1 入力に対する出力 の分布を取り出す t1 𝑥
- 51.
- 52. なぜ学習が失敗したのか 0 1 𝑥1 +𝑥2 2 𝑥1 𝑥1 𝑥2 𝑥2 𝑥1 + 𝑥2 2 t1 ここでは単純化のため, での期待値を とするt1 𝑥1 + 𝑥2 2
- 53. なぜ学習が失敗したのか 0 1 𝑥1 +𝑥2 2 𝑥1 𝑥1 𝑥2 𝑥2 𝑥1 + 𝑥2 2 t1 ここでは単純化のため, での期待値を とするt1 𝑥1 + 𝑥2 2 多峰性を持つ場合, 条件付き平均は解として不適
- 54. 教師有り学習の目標（再掲） これまでの仮定（多項式曲線フィッティングの例） ガウス分布は単峰性を持つため, 多峰性を持つ問題に対応できない. 単峰性 多峰性 目標：がどんな分布か知りたい（平均などのパラメータも含めて） 多峰性：極大値 が複数あること
- 55.
- 56.
- 57.
- 58. 混合密度ネットワークの構造 出力 決定するもの 個数 混合係数K カーネルの幅 K カーネルの中心 の要素 K×L (L+2)K個の出力ユニットが必要
- 59.
- 60.
- 61.
- 62.
- 63.
- 64.
- 65.
- 66.
- 67.
- 68.
- 69.
- 70.