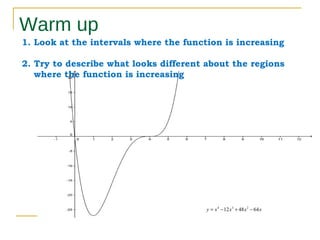
This document discusses using concavity and derivatives to understand the behavior of functions. It defines concavity as: - Concave up when the second derivative is positive, meaning the graph acceleration is positive. - Concave down when the second derivative is negative, meaning the graph acceleration is negative. Inflection points occur when the concavity changes, meaning the second derivative equals zero or is undefined. The document provides examples of using derivatives to determine concavity and find inflection points of functions.

1. Warm up
1. Look at the intervals where the function is increasing
2. Try to describe what looks different about the regions
where the function is increasing
y = x 4 − 12 x 3 + 48 x 2 − 64 x

2. Chapter Three: Section Four



The word we will use to describe the different
behaviors of the increasing regions of the function is
the word concavity.
When the second derivative of a function is positive,
we say that the function is concave up. What this
means physically is that the movement of the graph
has positive acceleration.
When the second derivative is negative then the
function is said to be concave down and this means
that the acceleration of the graph is negative.

3. Concavity

4. First derivative:
y′ is positive
Curve is rising.
y′ is negative
Curve is falling.
y′ is zero
Possible local maximum or
minimum.
Second derivative:
y′′ is positive
Curve is concave up.
y′′ is negative
Curve is concave down.
y′′ is zero
Possible inflection point
(where concavity changes).
→

5. Example Determining Concavity
Use the Concavity Test to determine the concavity of f ( x) = x on the
interval (2,8).
2
Since y " = 2 is always positive, the graph of y = x is concave
up on any interval. In particular, it is concave up on (2,8).
2

6. Inflection Point
1. Point where concavity changes
2. Point where second derivative changes
sign
3. POSSIBLY happen when f “ = 0
or f ’’ is undefined

8. Find the points of inflection and
discuss the concavity
1 4
3
f ( x) = x + 2 x
2

9. Find the points of inflection and
discuss the concavity
f ( x) = x − 4 x
4
3

10. Ex01: Determining Concavity
6
f ( x) = 2
x +3

11. Ex02: Determining Concavity
x +1
f ( x) = 2
x −4
2

12. Learning about Functions from
Derivatives