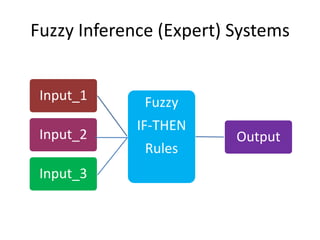
This document provides an overview of fuzzy logic and fuzzy set theory with examples from image processing. Some key points: - Fuzzy set theory was coined by Lofti Zadeh in 1965 and allows for degrees of membership rather than binary true/false values. Almost all real-world classes are fuzzy. - Fuzzy logic handles imprecise concepts like "tall person" through membership functions and handles inferences through generalized modus ponens. 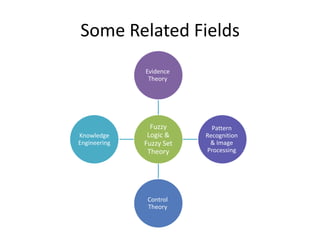- Fuzzy logic has been applied to fields like image processing, where concepts like "light blue" are fuzzy, and speech recognition by assigning fuzzy values to phonemes. 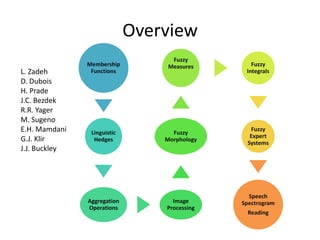- Techniques discussed include fuzzy membership functions, aggregation operations, alpha cuts, linguistic

1. Fuzzy Logic and Fuzzy Set Theorywith examples from Image ProcessingBy: Rafi Steinberg4/2/20081

2. Some Fuzzy BackgroundLoftiZadeh has coined the term “Fuzzy Set” in 1965 and opened a new field of research and applicationsA Fuzzy Set is a class with different degrees of membership. Almost all real world classes are fuzzy!Examples of fuzzy sets include: {‘Tall people’}, {‘Nice day’}, {‘Round object’} …If a person’s height is 1.88 meters is he considered ‘tall’?What if we also know that he is an NBA player? 2

3. Some Related Fields3

4. OverviewL. ZadehD. DuboisH. PradeJ.C. BezdekR.R. YagerM. SugenoE.H. MamdaniG.J. KlirJ.J. Buckley4

5. A Crisp Definition of Fuzzy LogicDoes not exist, however … - Fuzzifies bivalent Aristotelian (Crisp) logic Is “The sky are blue”True or False?Modus PonensIF <Antecedent == True> THEN <Do Consequent>IF (X is a prime number) THEN (Send TCP packet)Generalized Modus PonensIF “a region is green and highly textured” AND “the region is somewhat below a sky region”THEN “the region contains trees with high confidence”5

6. Fuzzy Inference (Expert) Systems6

7. Fuzzy Vs. ProbabilityWalking in the desert, close to being dehydrated, you find two bottles of water:The first contains deadly poison with a probability of 0.1The second has a 0.9 membership value in the Fuzzy Set “Safe drinks”Which one will you choose to drink from???7

8. Membership Functions (MFs)What is a MF? Linguistic VariableA Normal MF attains ‘1’ and ‘0’ for some inputHow do we construct MFs?HeuristicRank orderingMathematical ModelsAdaptive (Neural Networks, Genetic Algorithms …)8

9. Membership Function ExamplesSigmoidGaussianTrapezoidalTriangular9

10. Alpha CutsAlpha CutStrong Alpha Cut10

11. Linguistic HedgesOperate on the Membership Function (Linguistic Variable)Expansive (“Less”, ”Very Little”)Restrictive (“Very”, “Extremely”)Reinforcing/Weakening (“Really”, “Relatively”)11

12. Aggregation OperationsGeneralized Mean:12

13. Aggregation Operations (2)T-norms: Fixed Norms (Drastic, Product, Min)

14. Parametric Norms (Yager)S-Norm Duals:Bounded Sum DrasticZadehianDrasticProduct Zadehian13

15. Aggregation Operations (3)Yager S-Normb (=0.8)a (=0.3)Yager S-Norm for varying wGeneralized MeanDrasticT-NormZadehian minGeometricZadehian maxBoundedSumDrastic S-NormProductHarmonicAlgebraic (Mean)14

16. Crisp Vs. FuzzyFuzzy Sets Membership values on [0,1]Law of Excluded Middle and Non-Contradiction do not necessarily hold:Fuzzy Membership FunctionFlexibility in choosing the Intersection (T-Norm), Union (S-Norm) and Negation operationsCrisp SetsTrue/False {0,1}

17. Law of Excluded Middle and Non-Contradiction hold:Crisp Membership Function Intersection (AND) , Union (OR), and Negation (NOT) are fixed15

18. Image ProcessingBinaryGray LevelColor (RGB,HSV etc.)Can we give a crisp definition to light blue?16

19. Fuzziness Vs. VaguenessVagueness=Insufficient SpecificityFuzziness=Unsharp Boundaries17

20. Fuzziness“As the complexity of a system increases, our ability to make precise and yet significant statements about its behavior diminishes” – L. ZadehA possible definition of fuzziness of an image:18

21. Example: Finding an Image ThresholdMembership ValueGray Level19

22. Mathematical MorphologyOperates on predefined geometrical objects in an imageStructured Element (SE) represents the shape of interestInitially developed for binary images; extended to grayscale using aggregation operations from Fuzzy LogicSome Examples: Dilation, Erosion, Open, Close, Hit&Miss, Skeleton20

23. Fuzzy Mathematical Morphology“Does it fit” “How well does a SE fit”For B=021

24. Some Basic ConceptsUniverse of Discourse:Power Set of X= P(X)= {Null , {a} , {b} , {c} ,{a , b},{b , c}, {a , c}, {a,b,c}}Singletons of the Power Set of X: { {a} , {b} , {c} }An Event=An Element of the Power SetBasic Probability Assignment (BPA)Consonant Body of EvidenceFocal Elementm(A)=0.222

25. Fuzzy MeasuresAdditive, Sub Additive, Super Additive MeasuresExamples: {Probability}, {Belief, Plausibility}, {Necessity, Possibility}(1) Boundary Condition:(2) Monotonicity:(3) Uniform Convergenceincreasing sequence of measurable sets we have uniform convergence:23

26. Example: Fuzzy Measure24

27. The Choquet IntegralIs defined over a Fuzzy MeasureConsider a gray level input25

28. Example: Choquet Integral Calculation26

29. Sugeno MeasuresSugeno Measure’s Additional Axiom:Compute λ from the normalization rule:Sugeno Inverse:Sugeno Inverse for λ={-0.99, -0.9, -0.5, 0, 1, 10}Optimistic/Pessimistic Aggregation of Evidence27

30. Finding the Sugeno Measure We need to solve the third order equation: Solutions: {0, -15, 5/3} Since λ=0 is the trivial additive solution and since λ =-15 is out of range (λ>-1) we choose λ=5/3 and obtain:28

31. Example: Sugeno Integral Calculation-> We cannot aggregate with the Sugeno Union since the segmenting alpha cut values are not part of our initial frame of discernment-> Zadehian Max-Min are ‘good’ default operators29h(q) is the alpha cut that entirely includes the measure of q.

32. Example: Finding Edges30

33. O.K. So Now What?We have a fuzzy result, however in many cases we need to make a crisp decision (On/Off)Methods of defuzzifying are:Centroid (Center of Mass)MaximumOther methods31

34. Fuzzy Inference (Expert) SystemsFuzzify: Apply MF on inputGeneralized Modus Ponens with specified aggregation operationsDefuzzify: Method of Centroid, Maximum, ...32

35. Automatic Speech Recognition (ASR) via Automatic Reading of Speech SpectrogramsPhoneme Classes:VowelsSemi-vowels/DiphthongsNasalsPlosivesFricativesSilenceExamples of Fuzzy Variables:Distance between formants (Large/Small)Formant location (High/Mid/Low)Formant length (Long/Average/Short)Zero crossings (Many/Few)Formant movement (Descending/Ascending/Fixed)VOT= Voice Onset Time (Long/Short)Phoneme duration (Long/Average/Short)Pitch frequency (High/Low/Undetermined)Blob (F1/F2/F3/F4/None)“Don’t ask me to carry…"33

36. Applying the Segmentation Algorithm34

37. Suggested Fuzzy Inference SystemAssign a Fuzzy Value for each Phoneme, Output Highest N Values to a Linguistic modelOutput Fuzzy MF for each Phoneme35

38. Summary36Fuzzy Logic can be useful in solving Human related tasks