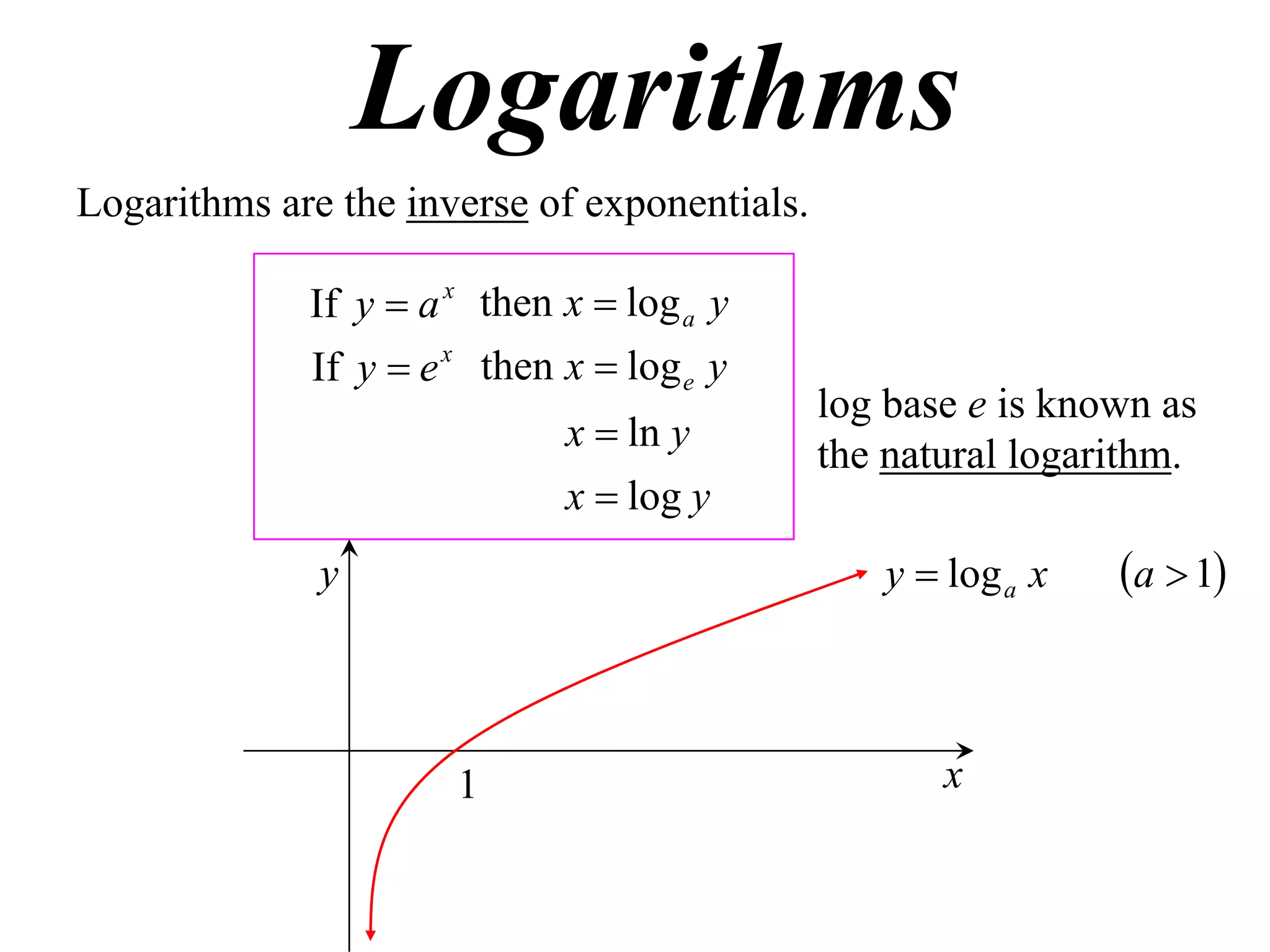
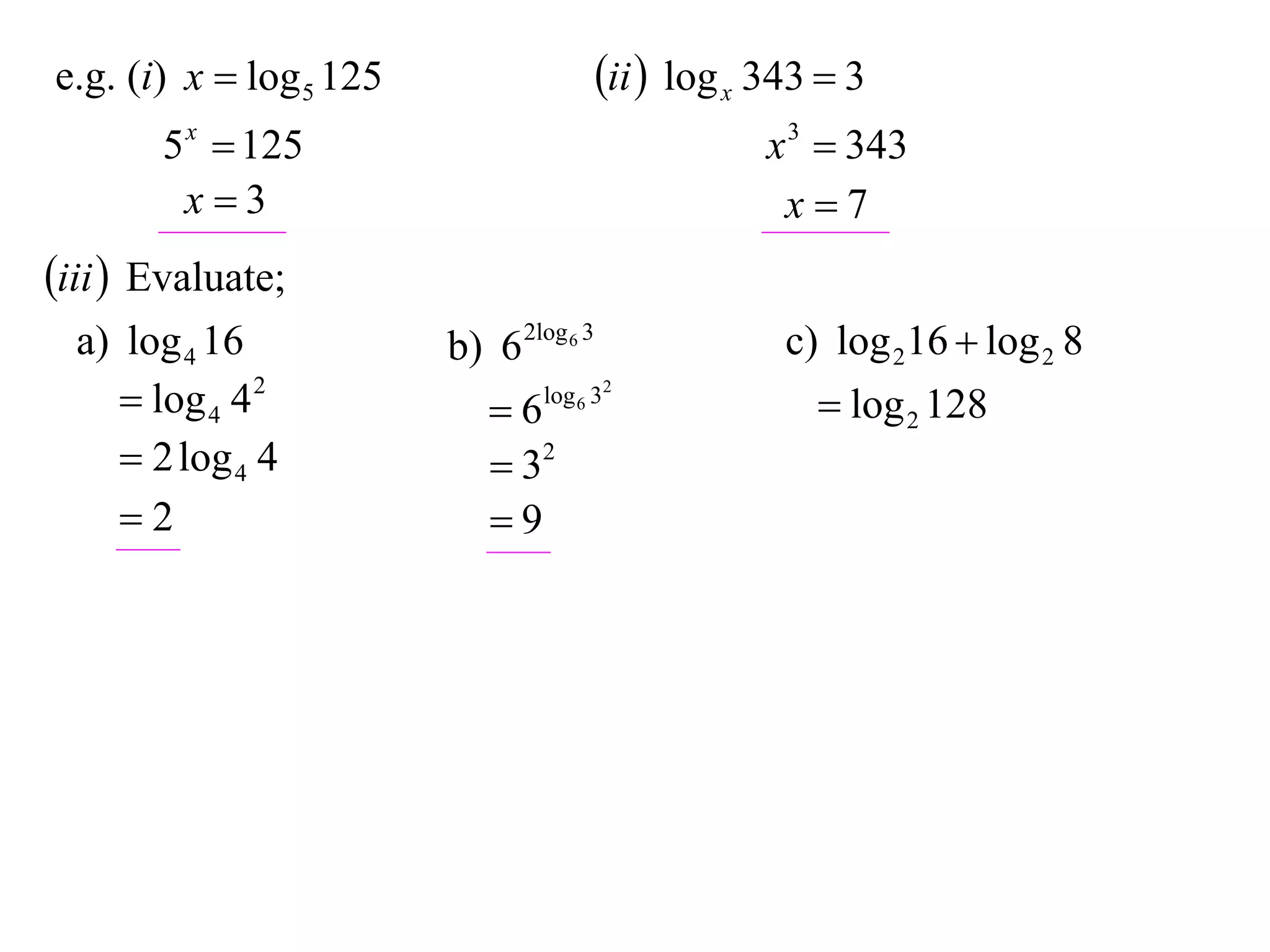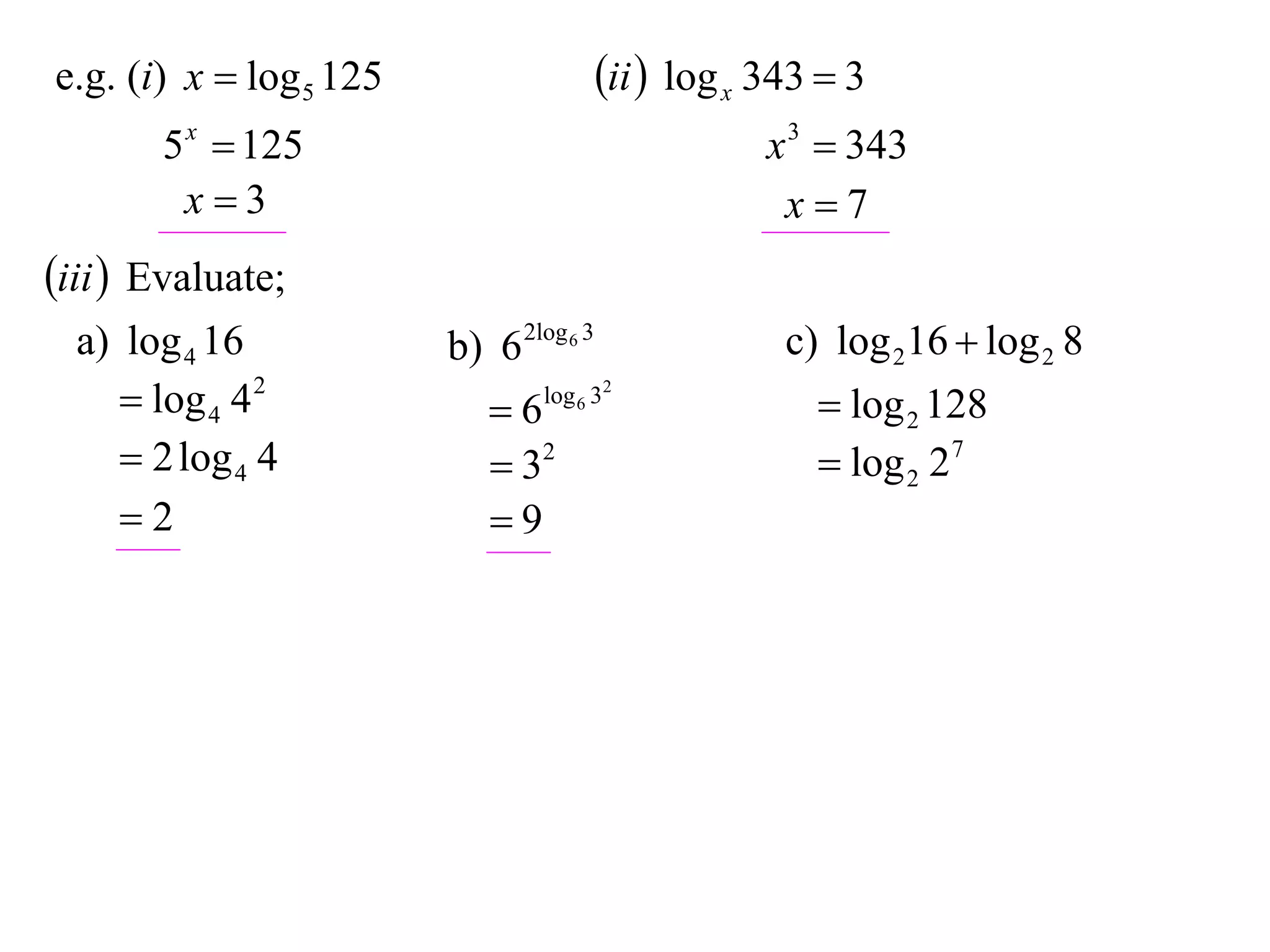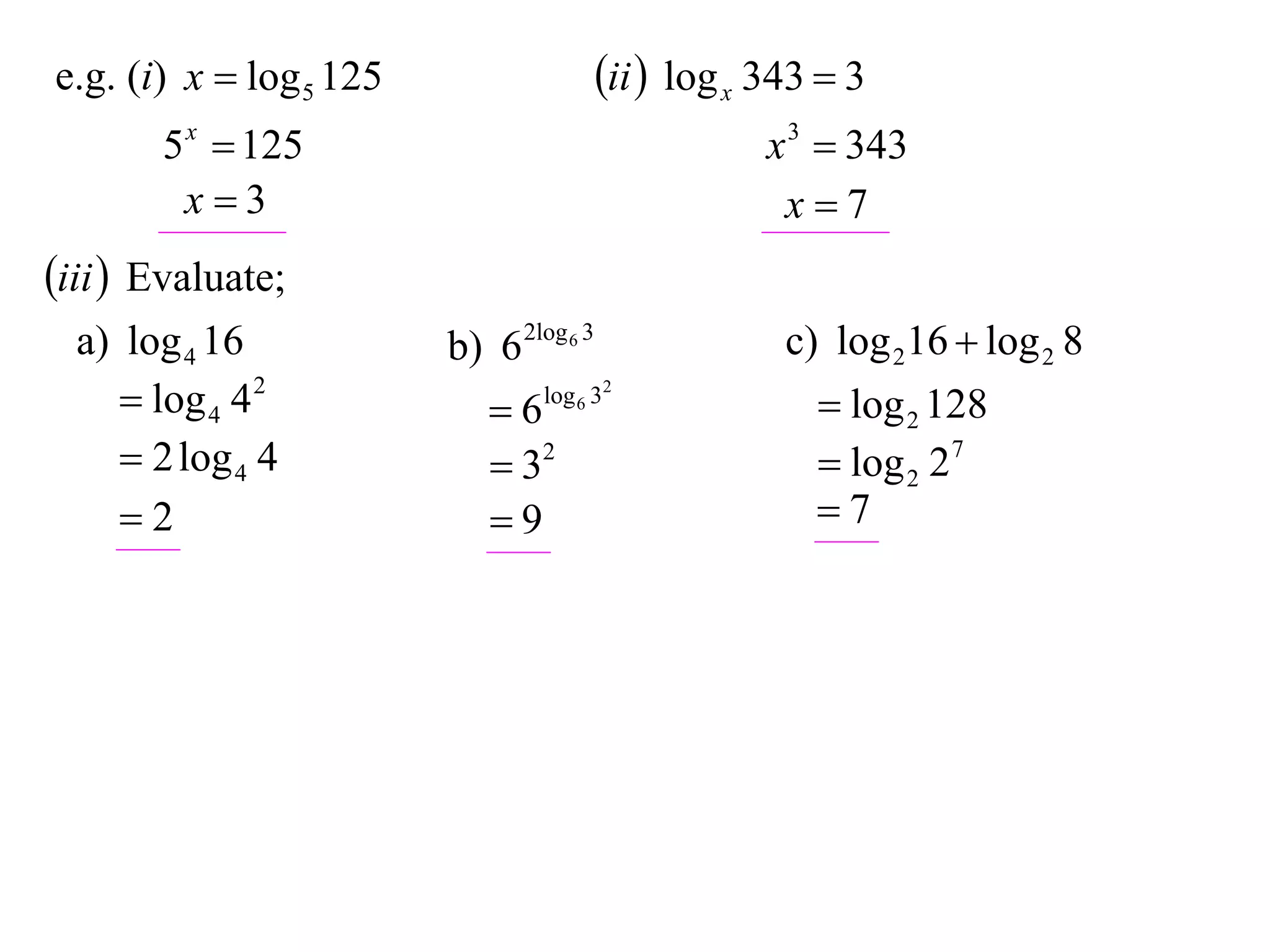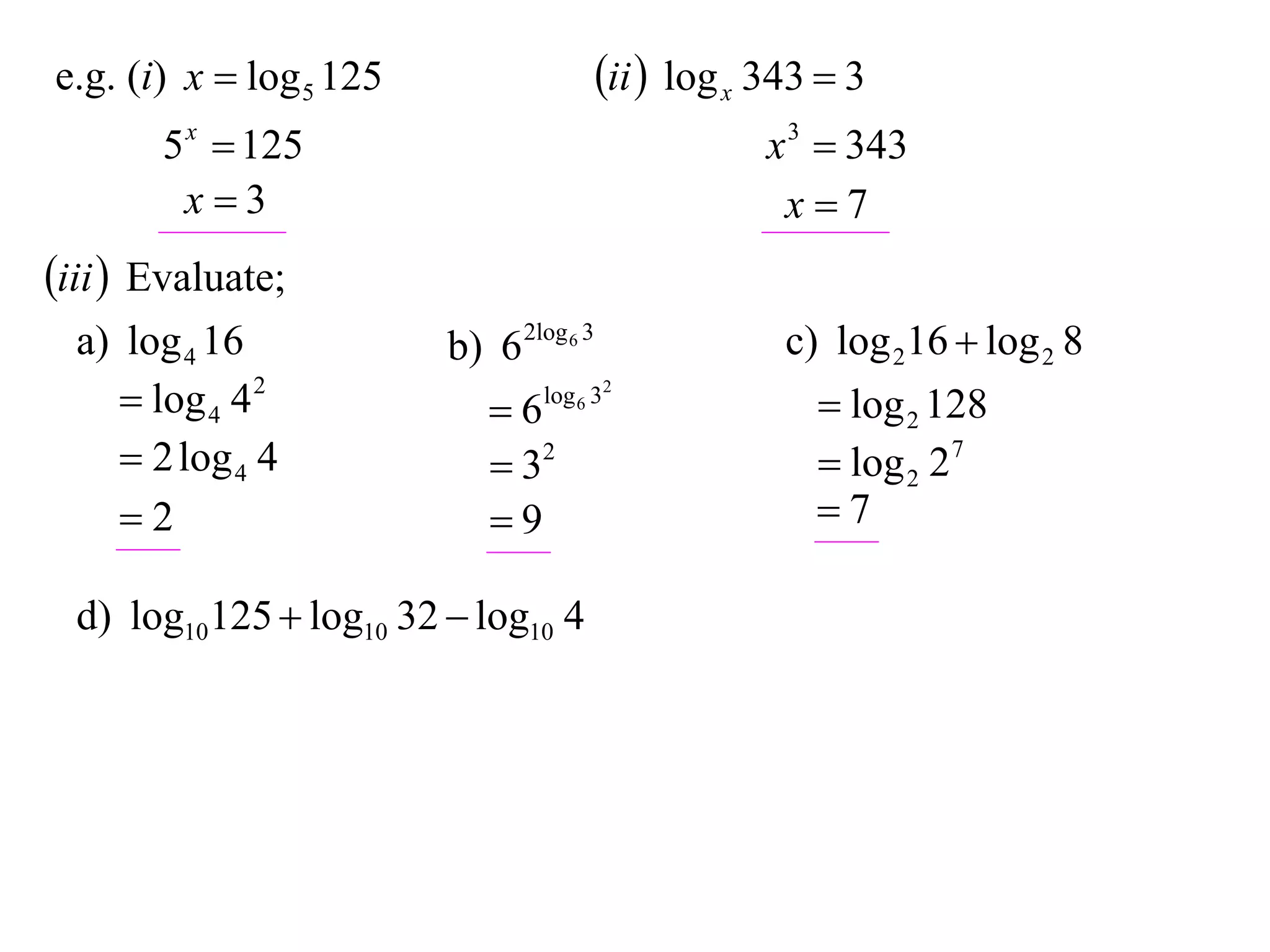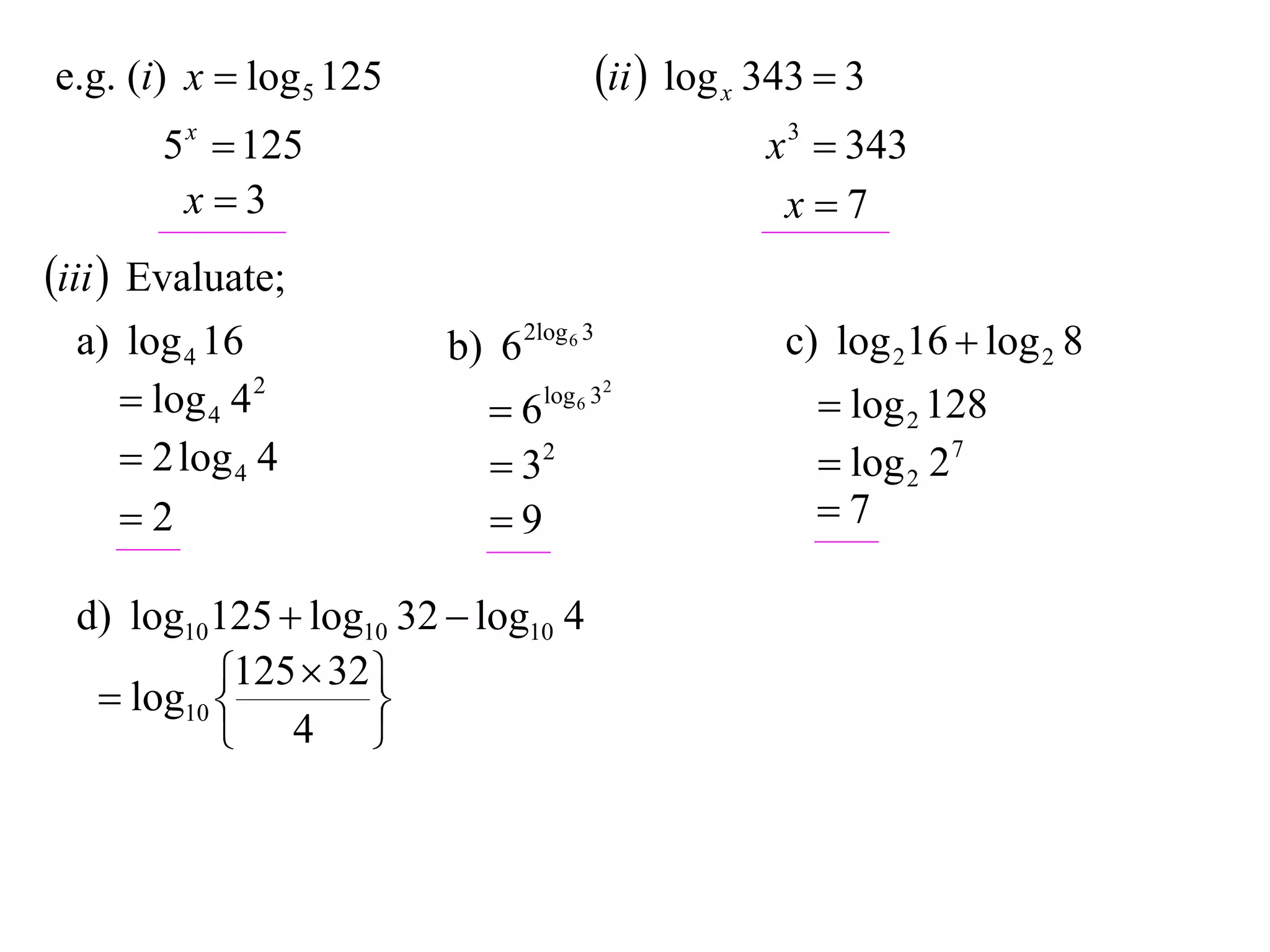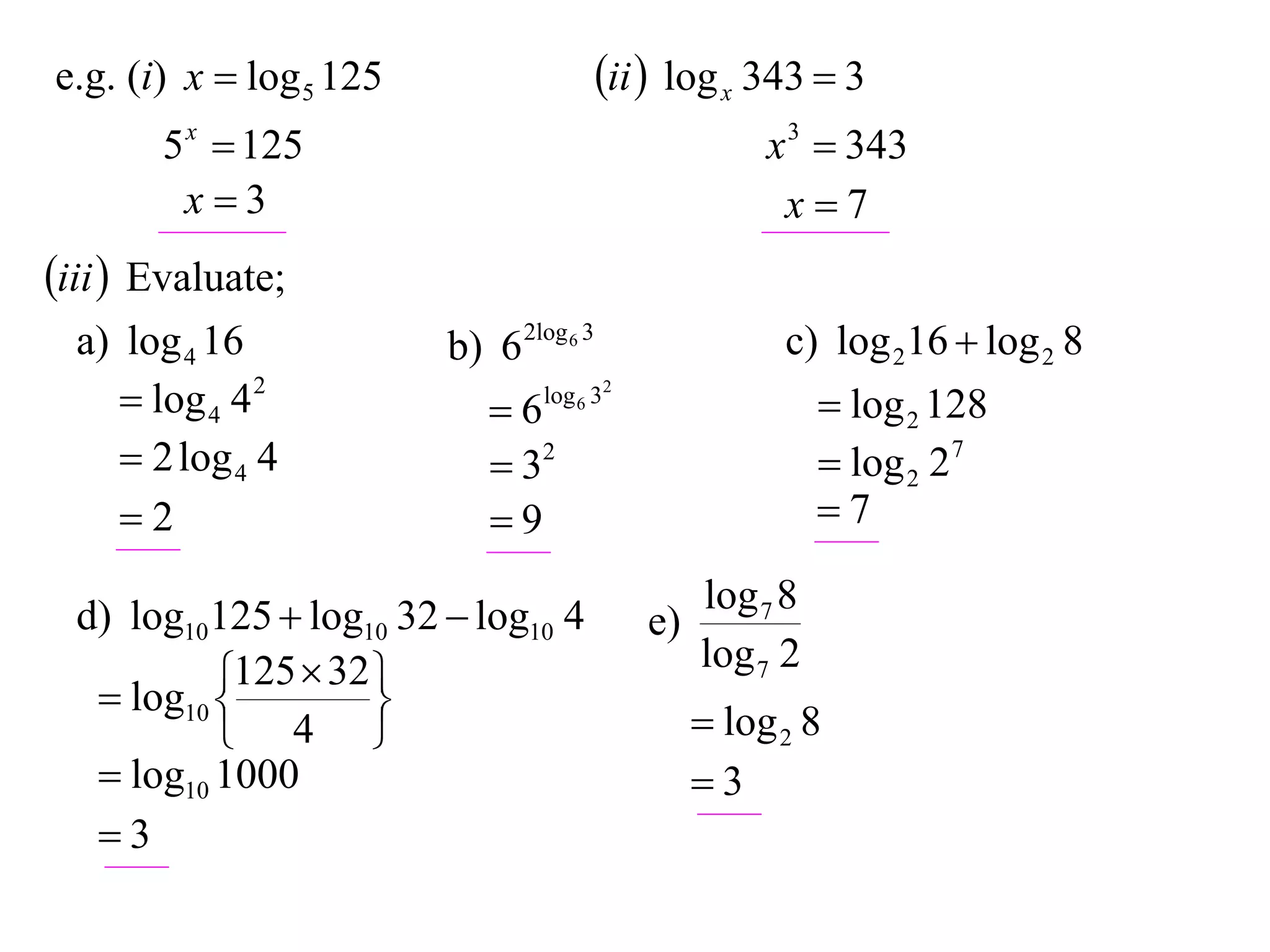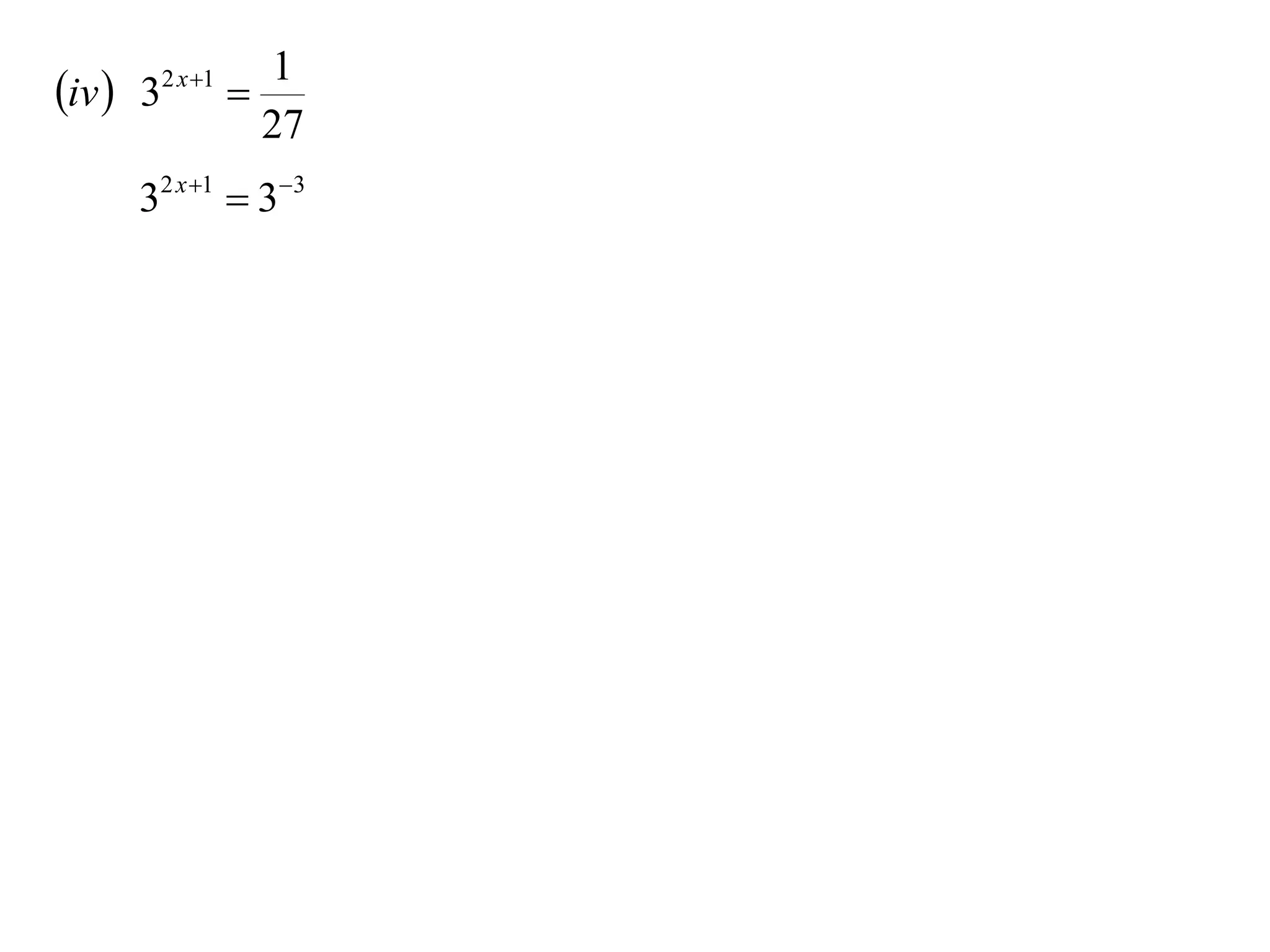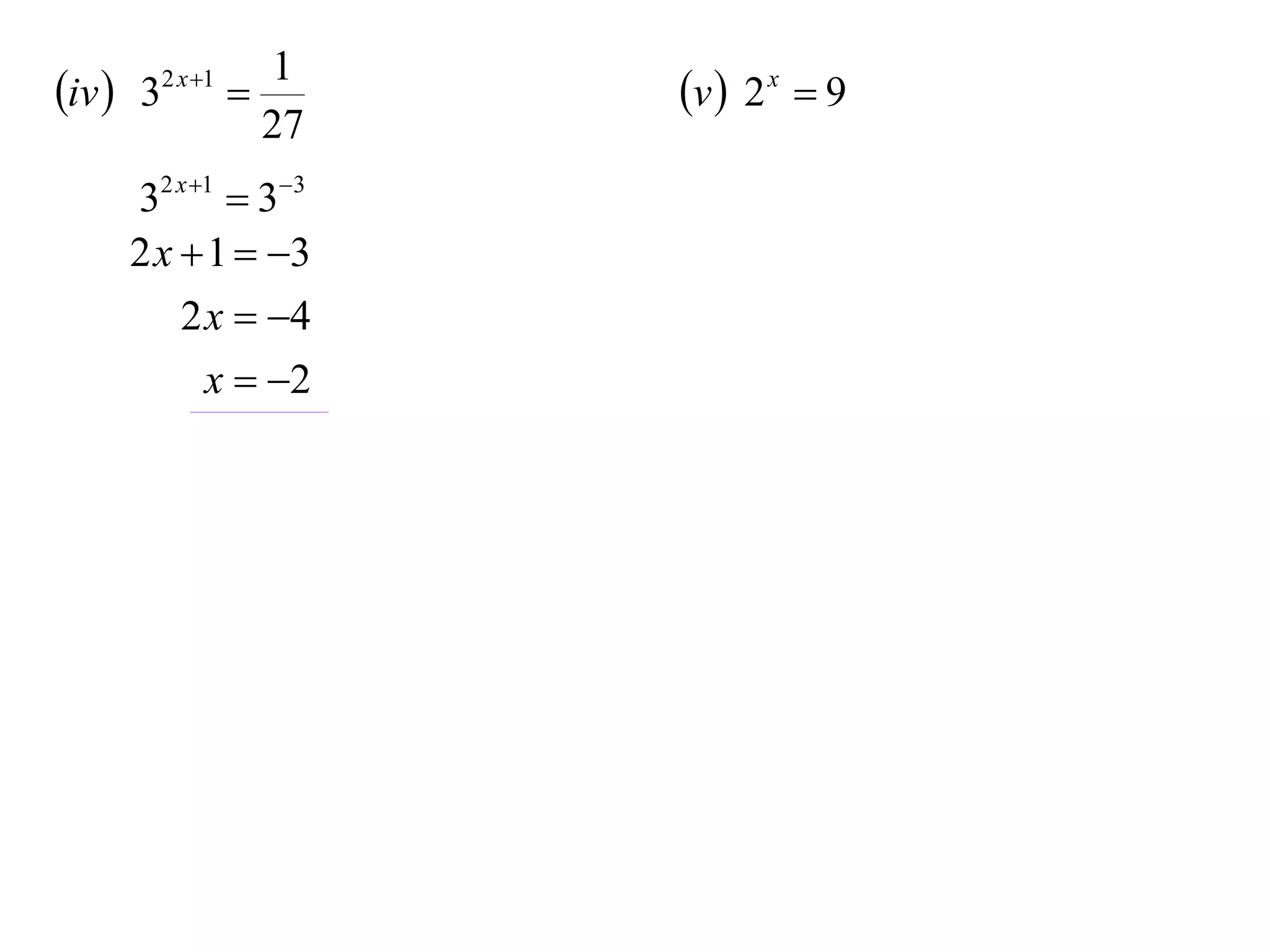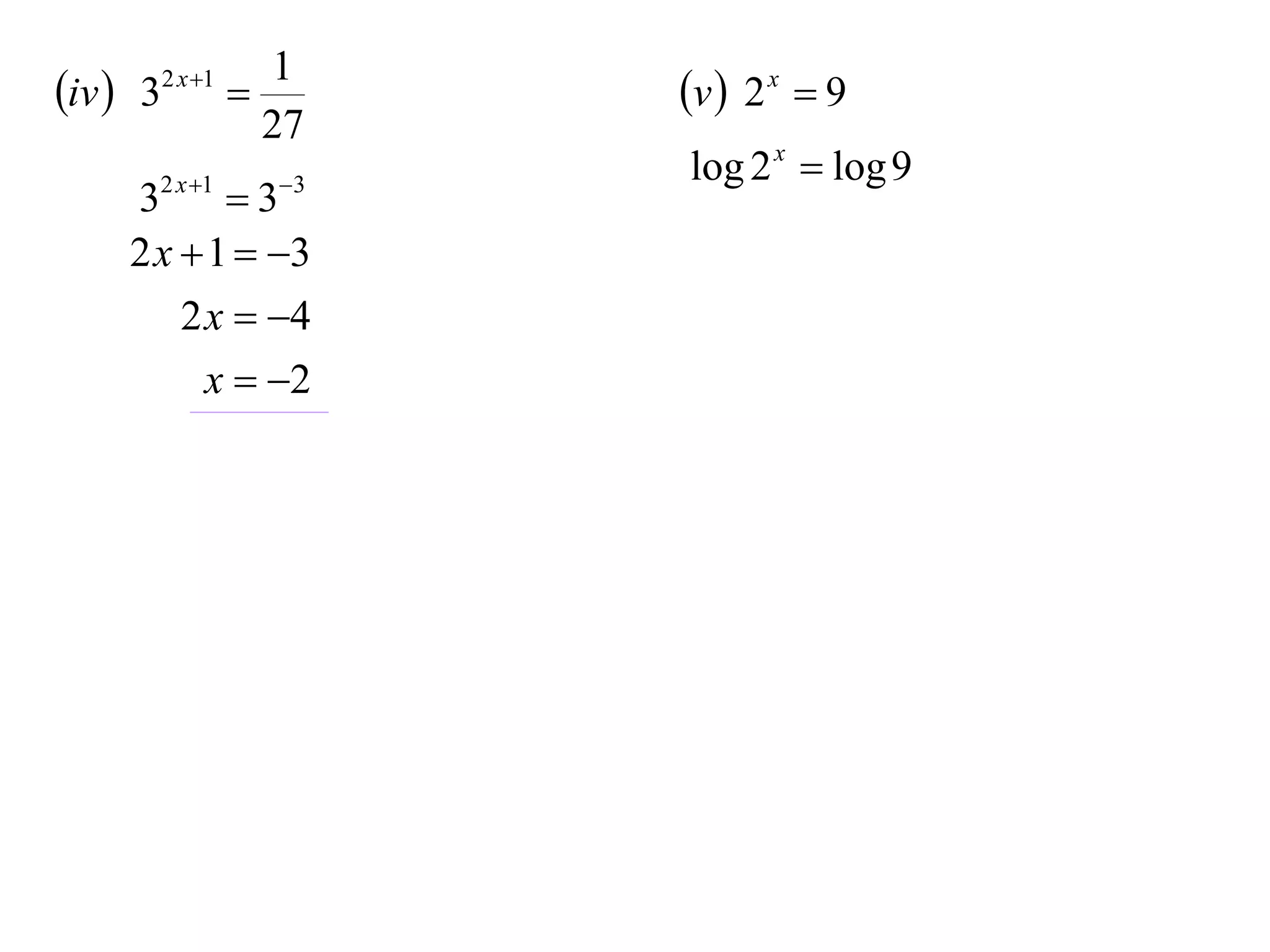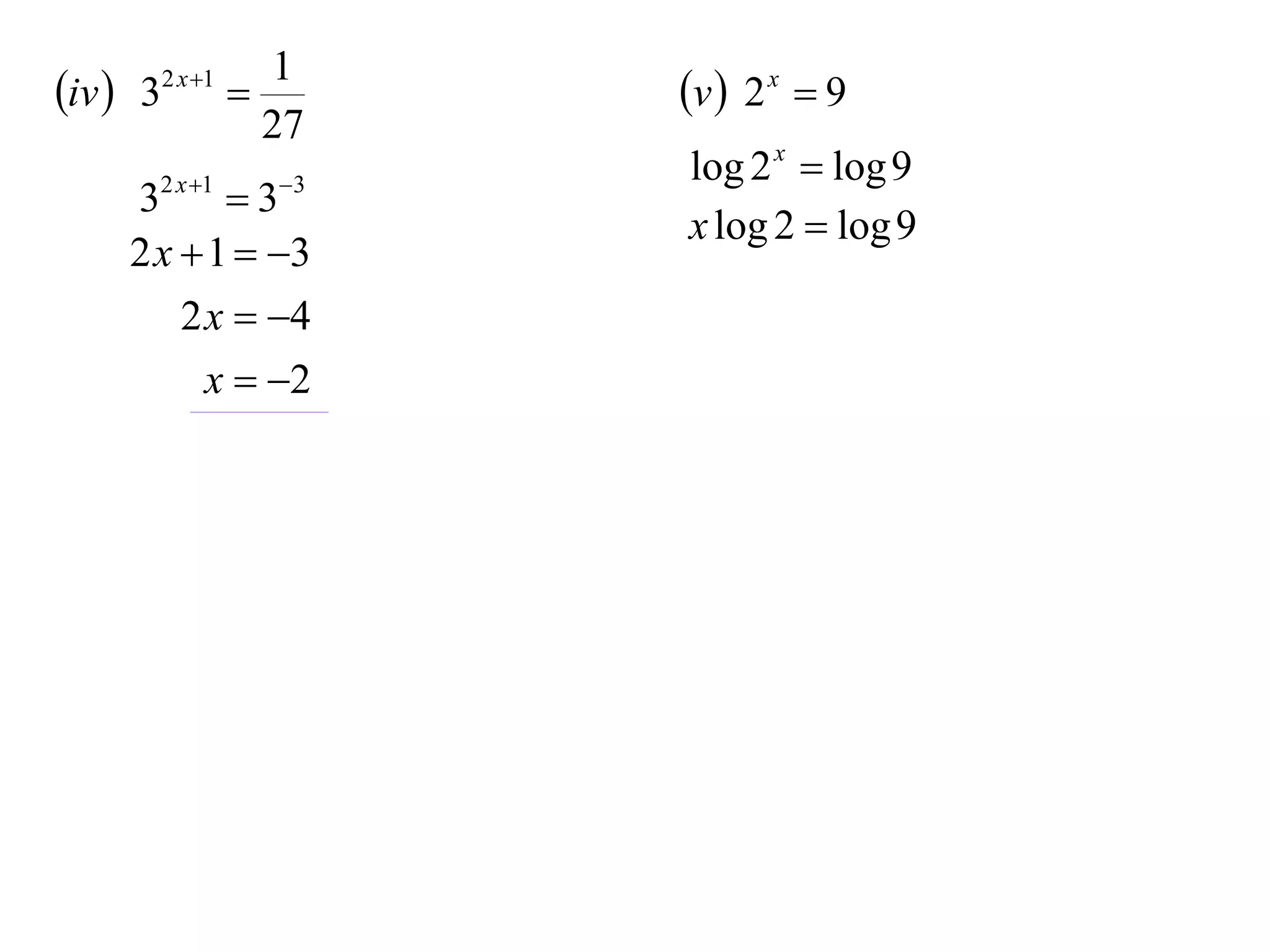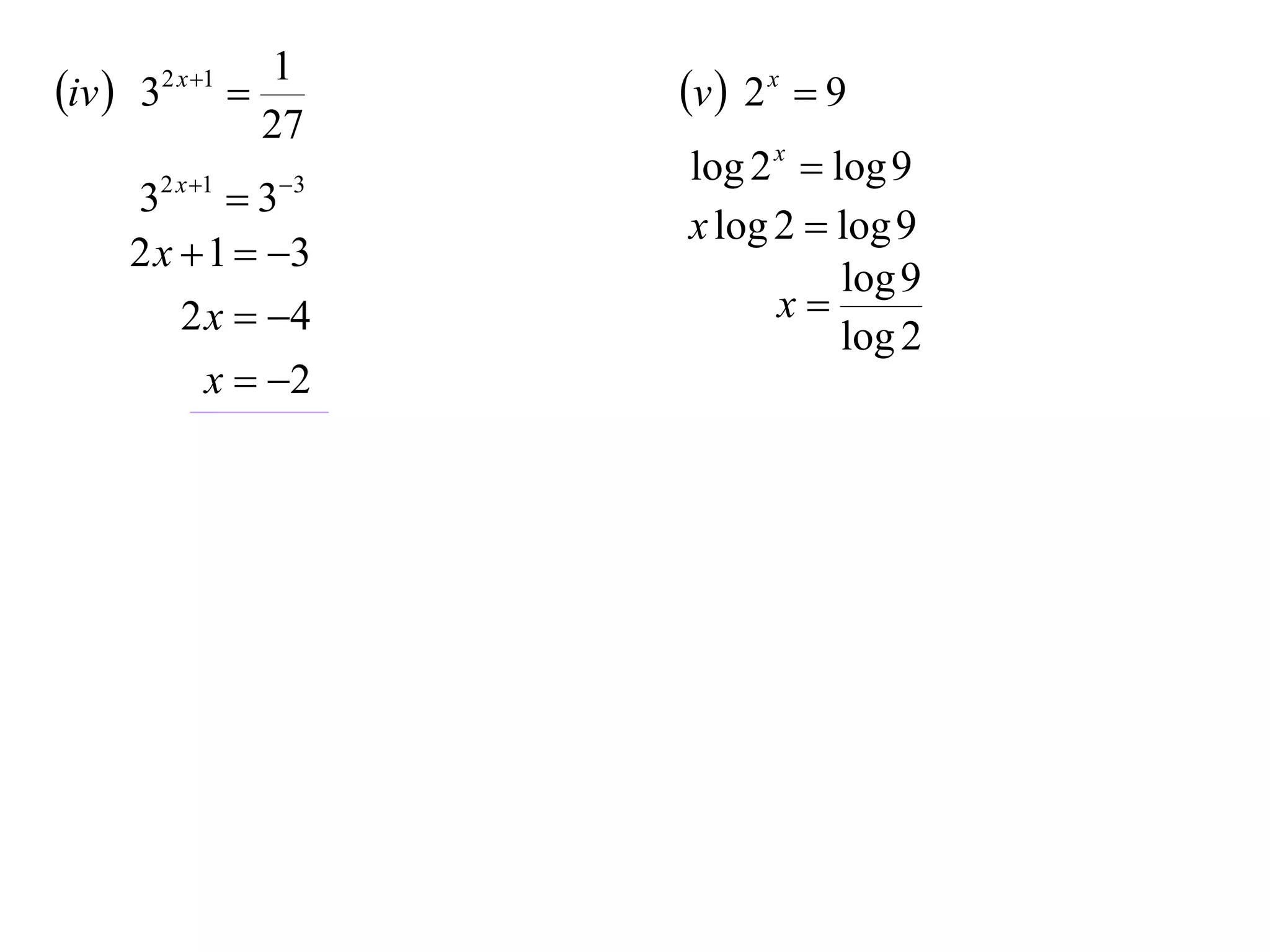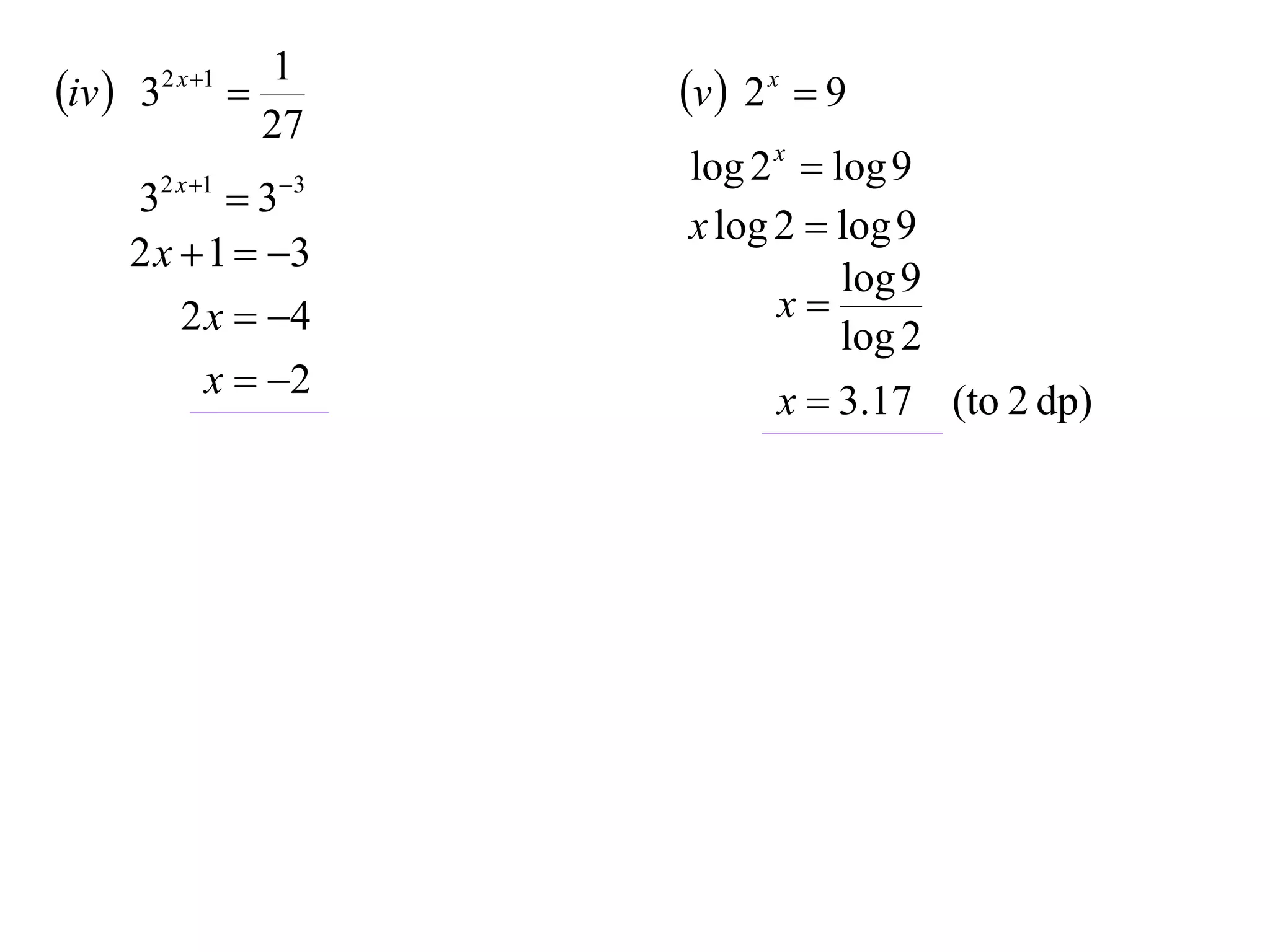The document discusses logarithms. Logarithms are the inverse of exponential functions. If y = ax, then x = loga y. The natural logarithm (ln) is the logarithm with base e. Logarithm laws and properties are presented, including the laws of logarithms, evaluating logarithmic expressions, and examples.

1. Logarithms

2. Logarithms
Logarithms are the inverse of exponentials.

3. Logarithms
Logarithms are the inverse of exponentials.
If y  a x

4. Logarithms
Logarithms are the inverse of exponentials.
If y  a x then x  log a y

5. Logarithms
Logarithms are the inverse of exponentials.
If y  a x then x  log a y
If y  e x

6. Logarithms
Logarithms are the inverse of exponentials.
If y  a x then x  log a y
If y  e x then x  log e y

7. Logarithms
Logarithms are the inverse of exponentials.
If y  a x then x  log a y
If y  e x then x  log e y
x  ln y

8. Logarithms
Logarithms are the inverse of exponentials.
If y  a x then x  log a y
If y  e x then x  log e y
x  ln y
x  log y

9. Logarithms
Logarithms are the inverse of exponentials.
If y  a x then x  log a y
If y  e x then x  log e y
log base e is known as
x  ln y
the natural logarithm.
x  log y

10. Logarithms
Logarithms are the inverse of exponentials.
If y  a x then x  log a y
If y  e x then x  log e y
log base e is known as
x  ln y
the natural logarithm.
x  log y
y y  log a x a  1
1 x

11. Logarithms
Logarithms are the inverse of exponentials.
If y  a x then x  log a y
If y  e x then x  log e y
log base e is known as
x  ln y
the natural logarithm.
x  log y
y y  log a x a  1
1 x
y  log a x 0  a  1

12. Logarithms
Logarithms are the inverse of exponentials.
If y  a x then x  log a y
If y  e x then x  log e y
log base e is known as
x  ln y
the natural logarithm.
x  log y
y y  log a x a  1
1 x
domain : x  0
y  log a x 0  a  1

13. Logarithms
Logarithms are the inverse of exponentials.
If y  a x then x  log a y
If y  e x then x  log e y
log base e is known as
x  ln y
the natural logarithm.
x  log y
y y  log a x a  1
1 x
domain : x  0
range : all real y y  log a x 0  a  1

14. Log Laws

15. Log Laws
1 log a m  log a n  log a mn

16. Log Laws
1 log a m  log a n  log a mn
m
2 log a m  log a n  log a  
n

17. Log Laws
1 log a m  log a n  log a mn
m
2 log a m  log a n  log a  
n
3 log a m n  n log a m

18. Log Laws
1 log a m  log a n  log a mn
m
2 log a m  log a n  log a  
n
3 log a m n  n log a m
4 log a 1  0

19. Log Laws
1 log a m  log a n  log a mn
m
2 log a m  log a n  log a  
n
3 log a m n  n log a m
4 log a 1  0
5 log a a  1

20. Log Laws
1 log a m  log a n  log a mn
m
2 log a m  log a n  log a  
n
3 log a m n  n log a m
4 log a 1  0
5 log a a  1
6 a log x  x
a

21. Log Laws
1 log a m  log a n  log a mn
m
2 log a m  log a n  log a  
n
3 log a m n  n log a m
4 log a 1  0
5 log a a  1
6 a log x  x
a
log b x
7  log a x 
log b a

22. e.g. (i) x  log 5 125

23. e.g. (i) x  log 5 125
5 x  125

24. e.g. (i) x  log 5 125
5 x  125
x3

25. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125
x3

26. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3

27. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7

28. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16

29. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16
 log 4 4 2

30. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16
 log 4 4 2
 2 log 4 4

31. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16
 log 4 4 2
 2 log 4 4
2

32. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3
 log 4 4 2
 2 log 4 4
2

33. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3
 log 4 4 2 6 log 6 32
 2 log 4 4
2

34. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3
 log 4 4 2 6 log 6 32
 2 log 4 4  32
2

35. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3
 log 4 4 2 6 log 6 32
 2 log 4 4  32
2 9

36. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 2 log 4 4  32
2 9

37. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32
2 9

38. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9

39. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7

40. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7
d) log10125  log10 32  log10 4

41. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7
d) log10125  log10 32  log10 4
125  32 
 log10 
 
 4 

42. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7
d) log10125  log10 32  log10 4
125  32 
 log10 
 
 4 
 log10 1000

43. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7
d) log10125  log10 32  log10 4
125  32 
 log10 
 
 4 
 log10 1000
3

44. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7
d) log10125  log10 32  log10 4 log 7 8
e)
125  32  log 7 2
 log10 
 
 4 
 log10 1000
3

45. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7
d) log10125  log10 32  log10 4 log 7 8
e)
125  32  log 7 2
 log10 
 
 4   log 2 8
 log10 1000
3

46. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7
d) log10125  log10 32  log10 4 log 7 8
e)
125  32  log 7 2
 log10 
 
 4   log 2 8
 log10 1000 3
3

47. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7 1
f) log 2
log 7 8 8
d) log10125  log10 32  log10 4 e)
125  32  log 7 2
 log10 
 
 4   log 2 8
 log10 1000 3
3

48. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7 1
f) log 2
log 7 8 8
d) log10125  log10 32  log10 4 e) 1 1
log 7 2  log 2
125  32 
 log10 
 
2 8
 4   log 2 8
 log10 1000 3
3

49. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7 1
f) log 2
log 7 8 8
d) log10125  log10 32  log10 4 e) 1 1
log 7 2  log 2
125  32 
 log10 
 
2 8
 4   log 2 8
 log10 1000 3
3

50. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7 1
f) log 2
log 7 8 8
d) log10125  log10 32  log10 4 e) 1 1
log 7 2  log 2
125  32 
 log10 
 
2 8
 4   log 2 8 1
 log10 1000   3
3 2
3

51. e.g. (i) x  log 5 125 ii  log x 343  3
5 x  125 x 3  343
x3 x7
iii  Evaluate;
a) log 4 16 b) 6 2log 6 3 c) log 216  log 2 8
 log 4 4 2 6 log 6 32
 log 2 128
 2 log 4 4  32  log 2 27
2 9 7 1
f) log 2
log 7 8 8
d) log10125  log10 32  log10 4 e) 1 1
log 7 2  log 2
125  32 
 log10 
 
2 8
 4   log 2 8 1
 log10 1000   3
3 2
3 3

2

52. 1
iv  32 x 1 
27

53. 1
iv  32 x 1 
27
32 x 1  33

54. 1
iv  32 x 1 
27
32 x 1  33
2 x  1  3
2 x  4
x  2

55. 1
iv  32 x 1  v  2 x  9
27
32 x 1  33
2 x  1  3
2 x  4
x  2

56. 1
iv  32 x 1  v  2 x  9
27
log 2 x  log 9
32 x 1  33
2 x  1  3
2 x  4
x  2

57. 1
iv  32 x 1  v  2 x  9
27
log 2 x  log 9
32 x 1  33
x log 2  log 9
2 x  1  3
2 x  4
x  2

58. 1
iv  32 x 1  v  2 x  9
27
log 2 x  log 9
32 x 1  33
x log 2  log 9
2 x  1  3
log 9
2 x  4 x
log 2
x  2

59. 1
iv  32 x 1  v  2 x  9
27
log 2 x  log 9
32 x 1  33
x log 2  log 9
2 x  1  3
log 9
2 x  4 x
log 2
x  2 x  3.17 (to 2 dp)

60. 1
iv  32 x 1  v  2 x  9
27
log 2 x  log 9
32 x 1  33
x log 2  log 9
2 x  1  3
log 9
2 x  4 x
log 2
x  2 x  3.17 (to 2 dp)
Exercise 12A; 2, 3aceg, 4bdfh, 5ab, 6ab, 7ac, 8bdh, 9ac, 14, 18*
Exercise 6B; 8