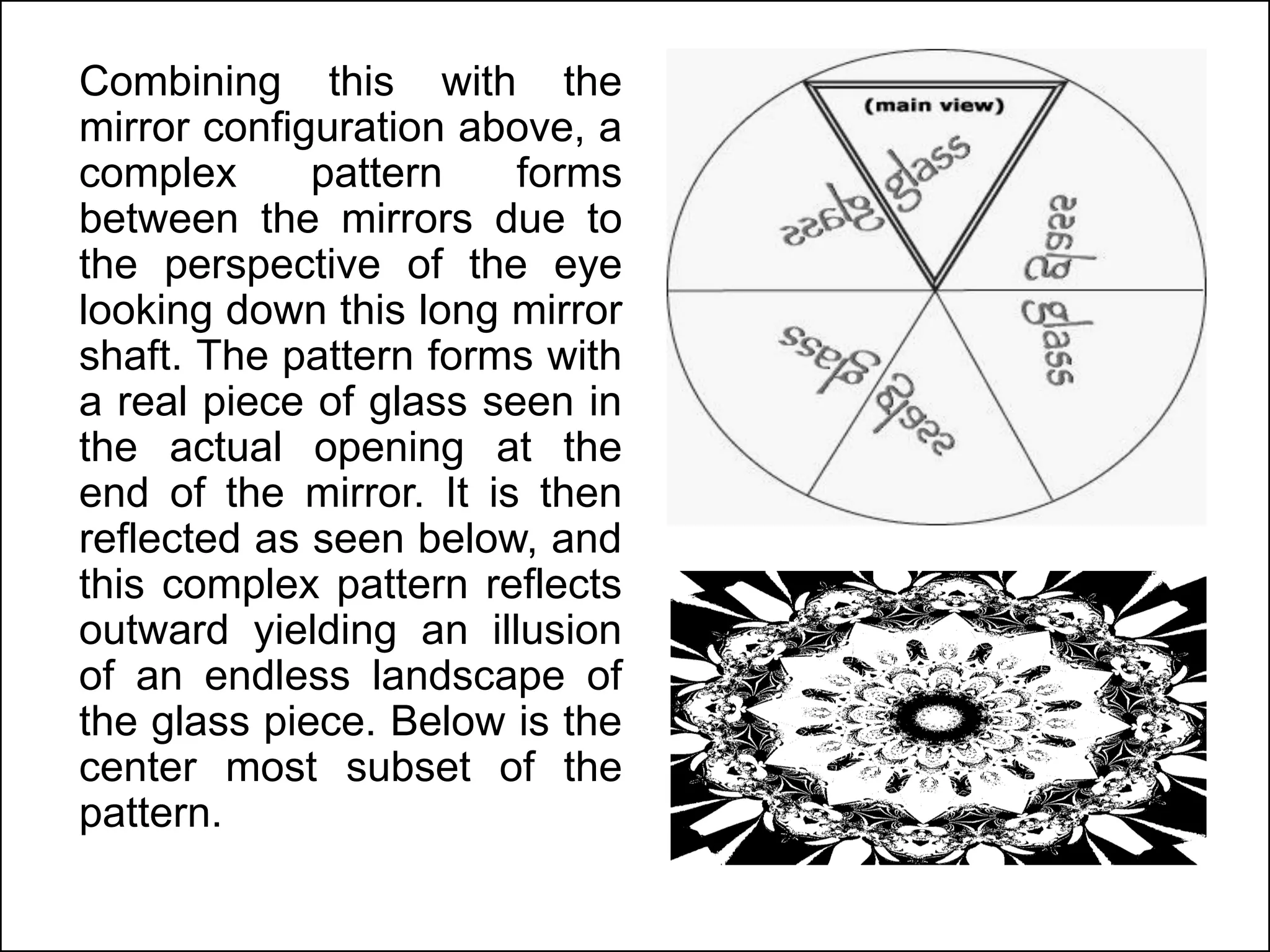
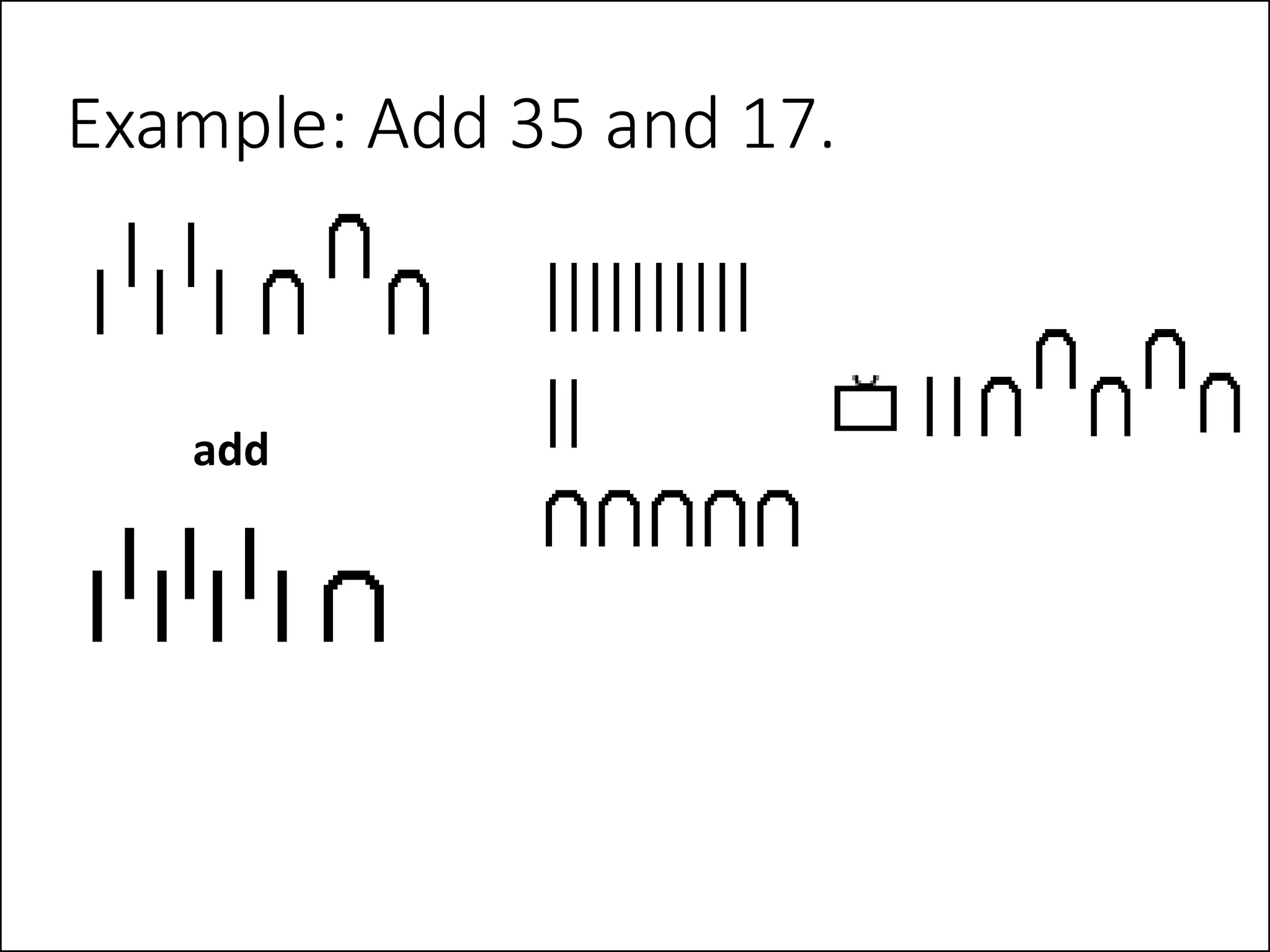
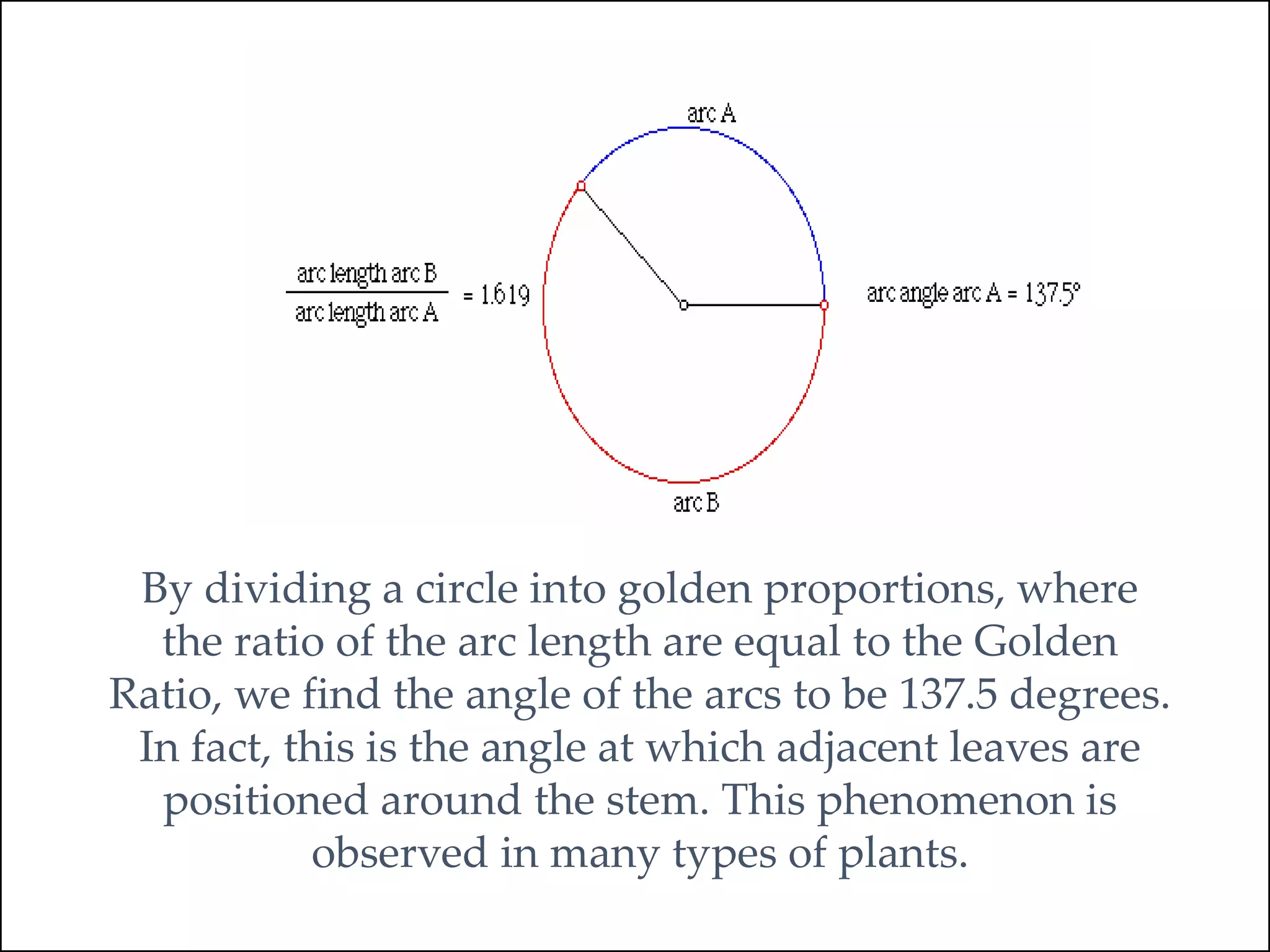
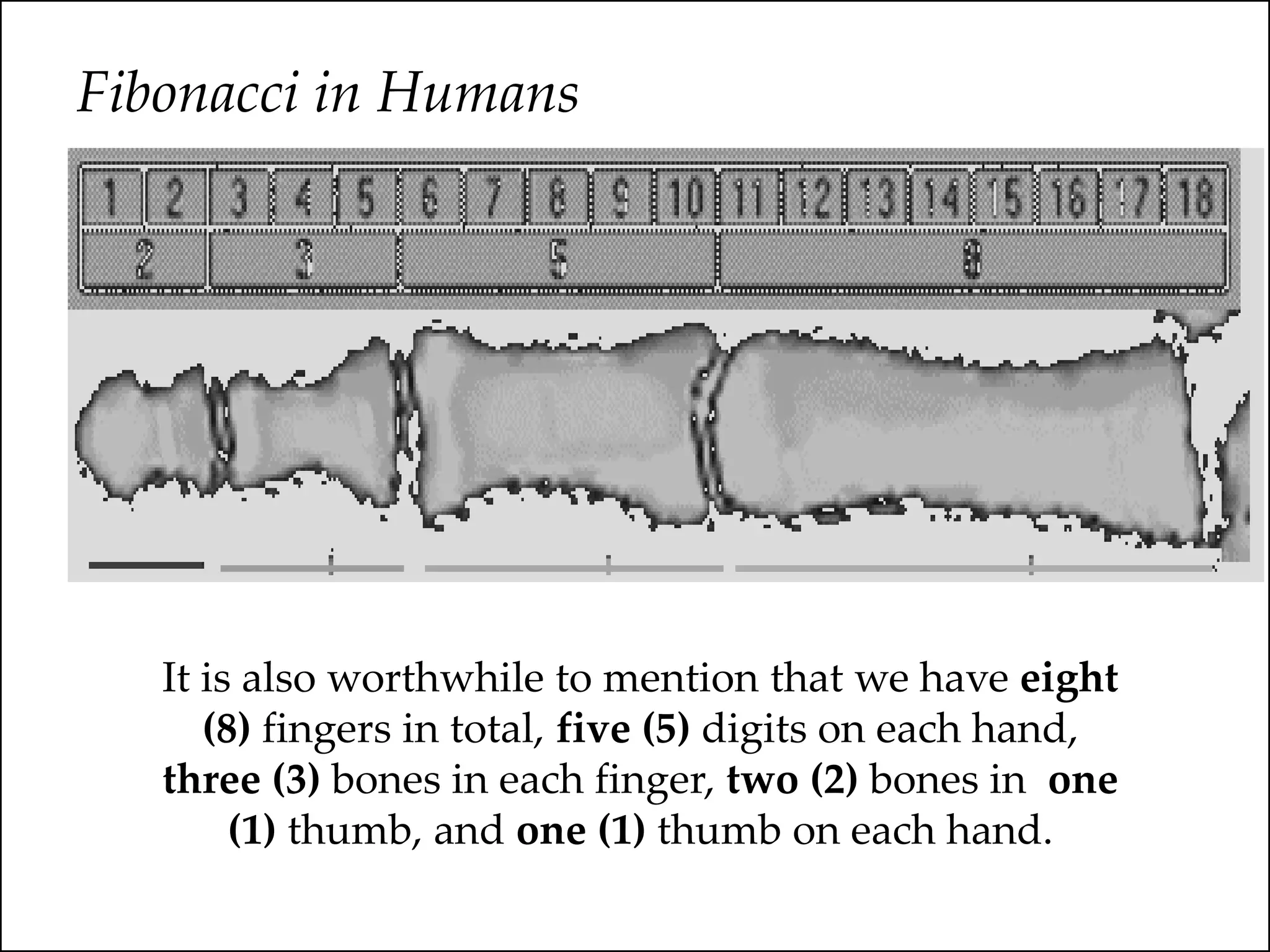
The document provides an overview of different types of fallacies in logic. It discusses semantic fallacies, which are errors due to ambiguity or incorrect construction of language. Examples of semantic fallacies given are equivocation, composition, and division. It also discusses material fallacies, which stem from issues with the subject matter itself. Examples of material fallacies provided are accident and confusing absolute and qualified statements. The document aims to define different logical fallacies and provide examples of each.

1. Mathematics
as Art

2. TOPICS TO BE COVERED:
•The Platonic solids and polyhedral
•The golden ratio and its applications:
a.Architecture
b.Painting
c. Book Design
• Applications of geometry like :
a. Kaleidoscopes
b. Mazes and labyrinths
c. The fourth dimension and
d. Optical illusions
• Music

4. The Platonic solids and Polyhedra

6. The Golden Ratio Then we have the golden ratio.
Looking at the rectangle we just drew,
you can see that there is a simple
formula for it. When one side is 1, the
other side will be:
The square root of 5 is approximately
2.236068, so The Golden Ratio is
approximately (1+2.236068)/2 =
3.236068/2 = 1.618034. This is an
easy way to calculate it when you
need it.

7. a. Architecture
• The Parthenon's façade as well as
elements of its façade and elsewhere
are said by some to be circumscribed
by golden rectangles. Other scholars
deny that the Greeks had any
aesthetic association with golden
ratio.
• Near-contemporary sources
like Vitruvius exclusively discuss
proportions that can be expressed in
whole numbers, i.e. commensurate as
opposed to irrational proportions.

8. b.Painting
•The drawing of a man's
body in a pentagram
suggests relationships to
the golden ratio.
•The 16th-century
philosopher Heinrich
Agrippa drew a man over
a pentagram inside a circle,
implying a relationship to
the golden ratio.[2]

9. Leonardo da Vinci's illustrations
of polyhedra in De divina
proportione (On the Divine
Proportion) and his views that
some bodily proportions exhibit
the golden ratio have led some
scholars to speculate that he
incorporated the golden ratio in
his paintings. But the suggestion
that his Mona Lisa, for
example, employs golden ratio
proportions, is not supported by
anything in Leonardo's own
writings. Similarly, although
the Vitruvian Man is often
shown in connection with the
golden ratio, the proportions of
the figure do not actually match
it, and the text only mentions
whole number ratios.

10. Salvador Dalí, influenced by
the works of Matila
Ghyka, explicitly used the
golden ratio in his
masterpiece, The Sacrament
of the Last Supper. The
dimensions of the canvas are
a golden rectangle. A huge
dodecahedron, in
perspective so that edges
appear in golden ratio to one
another, is suspended above
and behind Jesus and
dominates the composition.

11. c. Book design
•Depiction of the proportions in a medieval
manuscript. According to Jan Tschichold:
"Page proportion 2:3. Margin proportions
1:1:2:3. Text area proportioned in the Golden
Section."
•According to Jan Tschichold, there was a time
when deviations from the truly beautiful page
proportions 2:3, 1:√3, and the Golden Section
were rare. Many books produced between
1550 and 1770 show these proportions
exactly, to within half a millimeter.

12. Mazes and Labyrinths
• Many ornamental patterns
are related to topology, for
example mazes. Is there a
difference between a maze and a
labyrinth? Traditionally, the
terms have been considered to be
synonymous, but around 1990
people interested in the spiritual
aspects of labyrinths devised a
terminology where a labyrinth is
unicursal and a maze
multicursal. This means that a
labyrinth has only one path with
no branches and no dead ends, in
other words, no choice, while a
maze is a logical puzzle with
branches and possibly dead ends.

13. This maze appears in several medieval Hebrew manuscripts.
Although this maze has a superficial resemblance to the Cretan
maze, a close comparison shows they are quite different. The
Jericho maze has 7 levels, whereas the Cretan maze has 8, and
the sequence in which the levels are reached differs from one
maze to the other.
The best known of these mazes is the Cretan maze:
Jericho Maze:

14. OPTICAL ILLUSIONS
Geometrical-optical illusions are visual illusions, also optical
illusions, in which the geometrical properties of what is seen
differ from those of the corresponding objects in the visual
field.
Explanations of geometrical-optical illusion are based on one
of two modes of attack:
• the physiological or bottom-up, seeking the cause of the
deformation in the eye's optical imaging or in signal
misrouting during neural processing in the retina or the first
stages of the brain, the primary visual cortex, or
• the cognitive or perceptual, which regards the deviation from
true size, shape or position as caused by the assignment of a
percept to a meaningful but false or inappropriate object
class.

16. KALEIDOSCOPES
Three mirrors, generally from four or five to ten or twelve
inches long, and with a width of about an inch when the
length is 6 inches, and increasing in proportion as the
length increases, are put together at an angle of 60
degrees.
With one mirror, an object is reflected such that the angle of
incidence equals the angle of reflection.

17. Combining this with the
mirror configuration above, a
complex pattern forms
between the mirrors due to
the perspective of the eye
looking down this long mirror
shaft. The pattern forms with
a real piece of glass seen in
the actual opening at the
end of the mirror. It is then
reflected as seen below, and
this complex pattern reflects
outward yielding an illusion
of an endless landscape of
the glass piece. Below is the
center most subset of the
pattern.

18. FOUR-DIMENSIONAL SPACE
• In mathematics, four-dimensional space ("4D") is a
geometric space with four dimensions. It is typically meant to mean four-
dimensional Euclidean space, generalizing the rules of three-dimensional
Euclidean space. It has been studied by mathematicians and philosophers
for over two centuries, both for its own interest and for the insights it
offered into mathematics and related fields.
• Comparatively, 4-dimensional space has an extra coordinate axis,
orthogonal to the other three, which is usually labeled w. To describe the
two additional cardinal directions, Charles coined the terms ana and kata,
from the Greek words meaning "up toward" and "down from",
respectively. A length measured along the w axis can be called spissitude,
as coined by Henry More.

20. PROJECTIONS
• A useful application of dimensional analogy in visualizing
the fourth dimension is in projection. A projection is a way for
representing an n-dimensional object in n − 1 dimensions. For
instance, computer screens are two-dimensional, and all the
photographs of three-dimensional people, places and things are
represented in two dimensions by projecting the objects onto a
flat surface. When this is done, depth is removed and replaced
with indirect information. The retina of the eye is also a two-
dimensional array of receptors but the brain is able to perceive
the nature of three-dimensional objects by inference from
indirect information (such as shading, foreshortening, binocular
vision, etc.). Artists often use perspective to give an illusion of
three-dimensional depth to two-dimensional pictures.

21. Music
First octave
In music theory, the first octave, also
called the contra octave, ranges
from C1, or about 32.7 Hz, to C2, about
65.4 Hz, in equal temperament
using A440 tuning. This is the lowest
complete octave of
most pianos (excepting
the Bösendorfer Imperial Grand). The
lowest notes of instruments such
as double bass, electric bass, extended-
range bass clarinet, contrabass
clarinet, bassoon, contrabassoon, tuba a
nd sousaphone are part of the first
octave.

22. Ex: Siberian Throat Singers
The ability of vocalists to sing competently in the first octave is rare,
even for males. A singer who can reach notes in this range is known
as a basso profondo, Italian for "deep bass". A Russian bass can also
sing in this range, and the fundamental pitches sung by Tibetan
monks and the throat singers of Siberia and Mongolia are in this
range.

23. Mathematics
in History

24. Mathematics in
Ancient Egypt

25. Counting in Early Egypt
In ancient Egypt, texts would be written in Hieroglyphs. Their
number system always starts by 10. Their number one came from a
simple stroke. The number with two strokes and so on. The
numbers 10, 100, 1,000, 10,000 and 1,000,000 have their own
hieroglyphs. . Number 10 is a hobble for cattle, number 100 is
represented by a coiled rope, the number 1000 is represented by a
lotus flower, the number 10,000 is represented by a finger, the
number 100,000 is represented by a frog and a million was
represented by a god with his hands raised in adoration.

26. Addition in early Egypt
In adding two numbers, just add the
numbers then collect all symbols of
similar type and replace a ten of one
type by one of the next higher symbol.

27. Example: Add 35 and 17.
add

28. Subtraction in Early Egypt
Subtraction goes with the same but opposite process , For example:
Subtract 17 from 35.
Minus

29. Multiplication
in Early EgyptIn multiplying two numbers, all you needed to understand was the
double of the number.
For example:
multiply 35 by 11.
1 35
2 70
4 140
8 280
1 +2+8=11 35+70+280=385

30. Multiplication
in Early Egypt

31. Division in
Early EgyptIn Division, just do the reversal process of multiplication.
For example: divide 1075 by 25
1 25
2 50
4 100
8 200
16 400
32 800
1+2+8+32= 43 25+50+200+800= 1075

32. Division in
Early Egypt

33. SUMMARY
•Mathematics in Ancient Egypt is
composed of four main operation.
Addition, subtraction, multiplication
and division which is also used
nowadays. The only difference is
instead of numbers they use
symbols called
hieroglyphics/counting glyphs.

34. Patterns in
Real Life

35. Objectives:
 To cite examples of some
applications of mathematics in our
everyday lives.
 To define the meanings of the
different mathematical patterns
applied to our daily lives.
 To prove that mathematics has
importance not only in science but in
our surroundings as well.

36. Topics to be Covered:
 Number Patterns
o Arithmetic Sequence
o Geometric Sequence
oFibonacci Sequence
Fibonacci in Nature
o Fibonacci in Plants
oFibonacci in Animals
oFibonacci in Humans

37. Number Patterns
o Arithmetic Sequence
An arithmetic sequence has a constant difference
between terms. The first term is a1, the common
difference is d, and the number of terms is n.
Explicit Formula:
an = a1 + (n – 1)d

38. o Geometric Sequence
A geometric sequence has a constant ratio between
terms. The first term is a1, the common ratio is r,
and the number of terms is n.
Explicit Formula:
an = a1rn-1
o Fibonacci Sequence
The sequence of numbers which the
next term is found by adding the previous two
terms.

39. Fibonacci in Nature
The Fibonacci numbers are nature's numbering
system. They appear everywhere in nature,
from the leaf arrangement in plants, to the
pattern of the florets of a flower, the bracts of a
pinecone, or the scales of a pineapple. The
Fibonacci numbers are therefore applicable to
the growth of every living thing, including a
single cell, a grain of wheat, a hive of bees,
and even all of mankind.

40. Why do these arrangements occur?
In the case of leaf arrangement, or phyllotaxis, some of
the cases may be related to maximizing the space for
each leaf, or the average amount of light falling on
each one. Even a tiny advantage would come to
dominate, over many generations. In the case of
close-packed leaves in cabbages and succulents the
correct arrangement may be crucial for availability of
space.
In the seeming randomness of the natural world, we
can find many instances of mathematical order
involving the Fibonacci numbers themselves and the
closely related “golden" elements.

41. Fibonacci in Plants
Phyllotaxis is the study of
the ordered position of
leaves on a stem. The
leaves on this plant are
staggered in a spiral
pattern to permit
optimum exposure to
sunlight. If we apply the
Golden Ratio to a circle
we can see how it is that
this plant exhibits
Fibonacci qualities.

42. By dividing a circle into golden proportions, where
the ratio of the arc length are equal to the Golden
Ratio, we find the angle of the arcs to be 137.5 degrees.
In fact, this is the angle at which adjacent leaves are
positioned around the stem. This phenomenon is
observed in many types of plants.

43. Inside the fruit of many plants we can observe the
presence of Fibonacci order.
The banana has three (3)
sections
The apple has five (5)
sections

44. Fibonacci in Animals
The shell of the chambered Nautilus
has Golden proportions. It is a
logarithmic spiral.
The eyes, fins and tail of the dolphin
fall at golden sections along the
body.
A starfish has 5 arms.

45. Fibonacci in Humans
It is also worthwhile to mention that we have eight
(8) fingers in total, five (5) digits on each hand,
three (3) bones in each finger, two (2) bones in one
(1) thumb, and one (1) thumb on each hand.

46. Fallacies
in Logic

47. What are Fallacies?
A fallacy is an argument that uses
poor reasoning. An argument can
be fallacious whether or not its
conclusion is true.

48. • Semantic Fallacies – are those which
have to do with errors due to ambiguity in
the meaning of words used or errors due
to confusion resulting from incorrect
grammatical construction, or judgment or
reasoning.

49. Types of Semantic Fallacies
 Fallacy of Equivocation –
committed when one assumes that
words that have the same spelling or
sound are used with the same
meaning in an argument.

50. Examples:
• Star is a heavenly body,
but Elizabeth is a star,
therefore, Elizabeth is a heavenly
body
• Light comes from the sun,
but feathers are light,
hence, feathers come from the sun

51.  Fallacy of Composition –
taking ideas or things together
when they should be taken
separately or individually.
Example:
Aliens and those below 18 years are
not eligible to vote,
but I should be allowed to vote
because while I am an alien I am of
voting age.

52.  Fallacy of Division – is the opposite
of fallacy of composition and results
from taking ideas or things
separately when they should be
taken collectively.
Example:
All his merchandise cost P500,
but his ballpoint pen is part of his merchandise
therefore, his ballpoint pen costs P500

53. •Material Fallacies – have to
do with errors which have to
do with errors which spring
from inattention or abuse of
the subject matter or
content of an argument.

54. Types of Material Fallacies
 Fallacy of Accident – consists in
arguing that what is affirmed or denied
of a thing under accidental condition
can also be affirmed or denied of its
essential nature.
Example:
A person who is drunk is irrational,
but this person is drunk,
therefore this person is irrational.

55.  Fallacy of Confusing the Absolute and
Qualified Statement – is the result of
concluding that a qualified statement is
true because the absolute statement is
true, or that the absolute statement is true
because the qualified statement is true.
Example:
Filipinos are hospitable,
this person is a Filipino,
hence, this person is hospitable