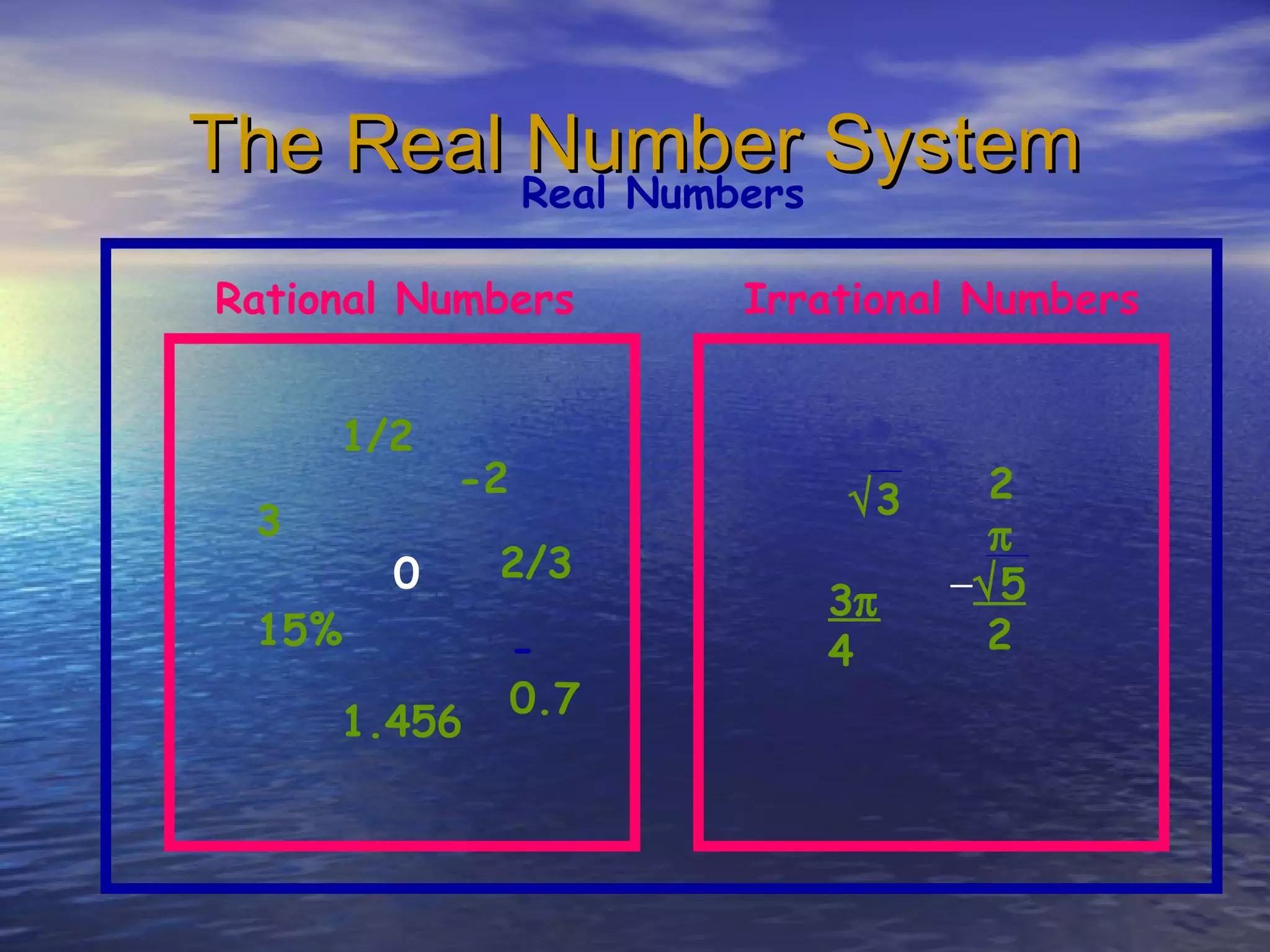
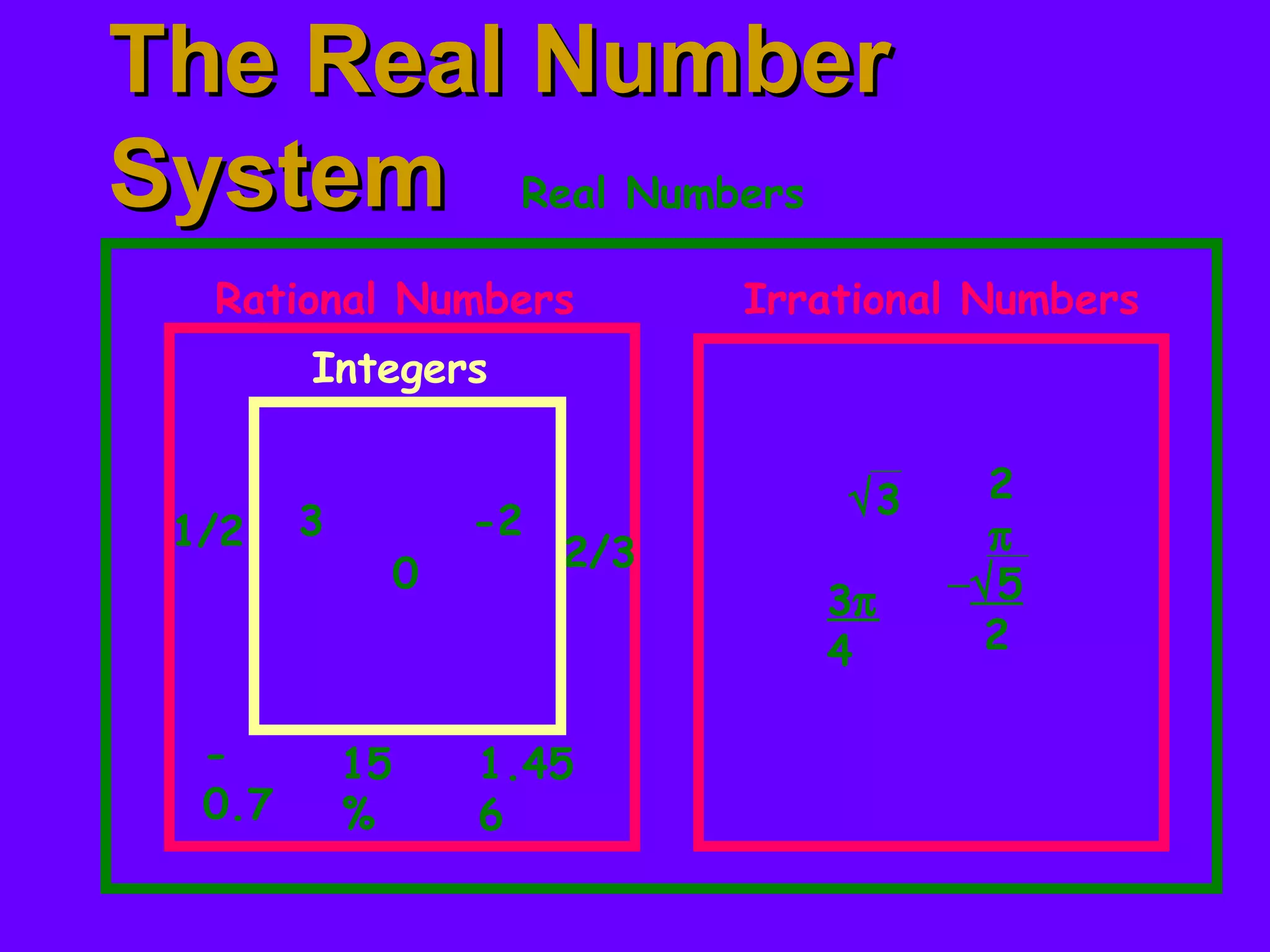
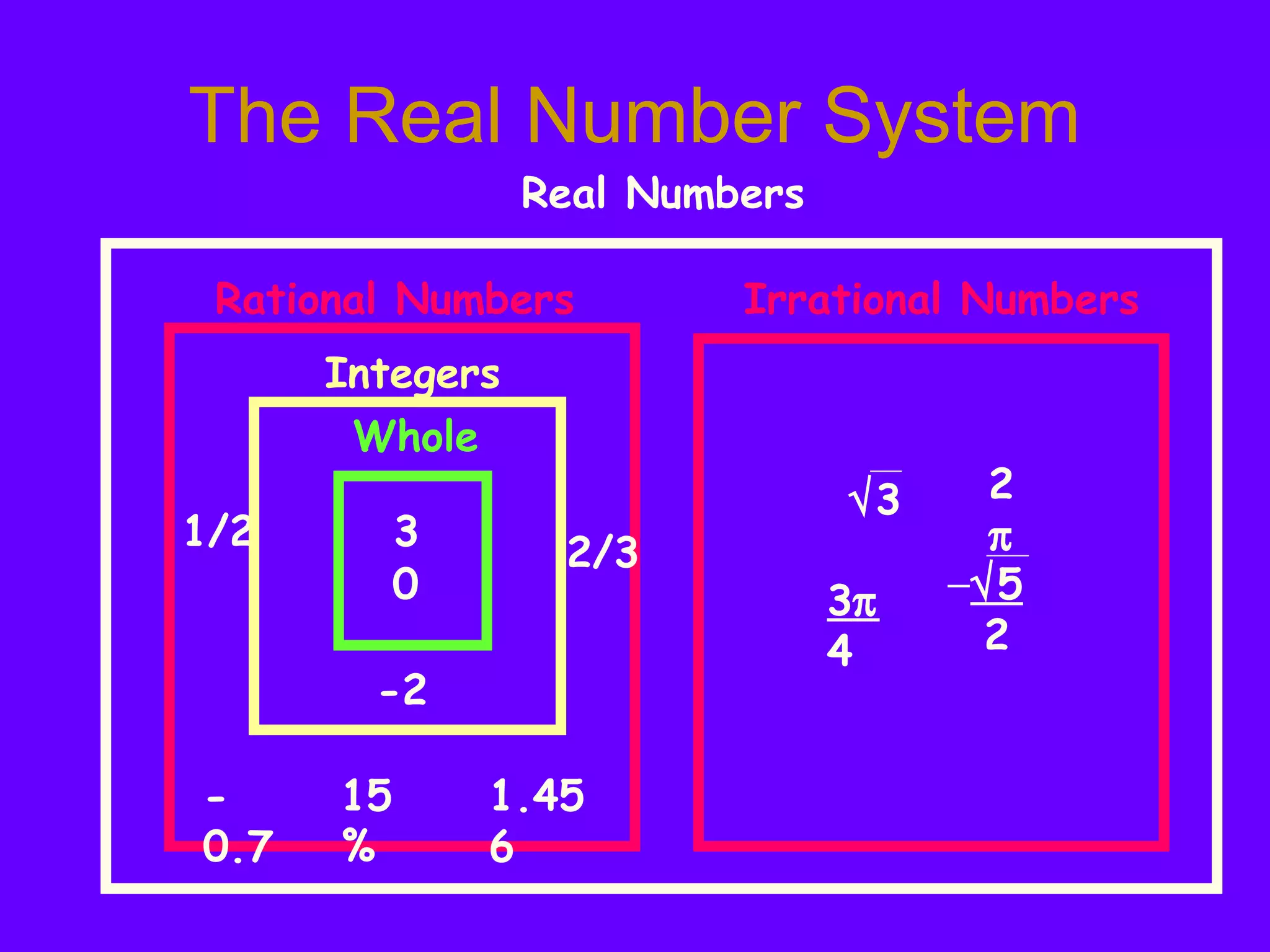
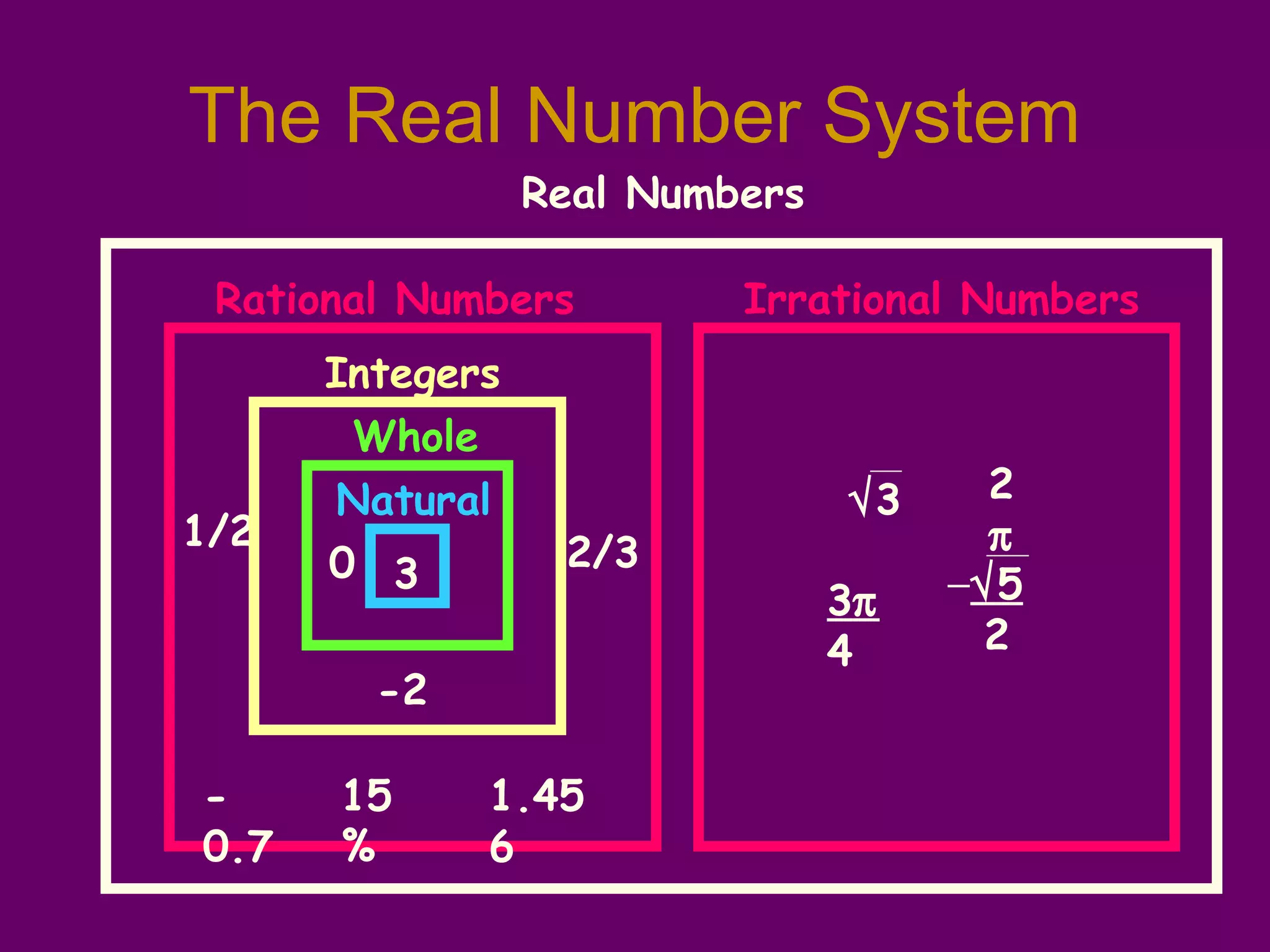
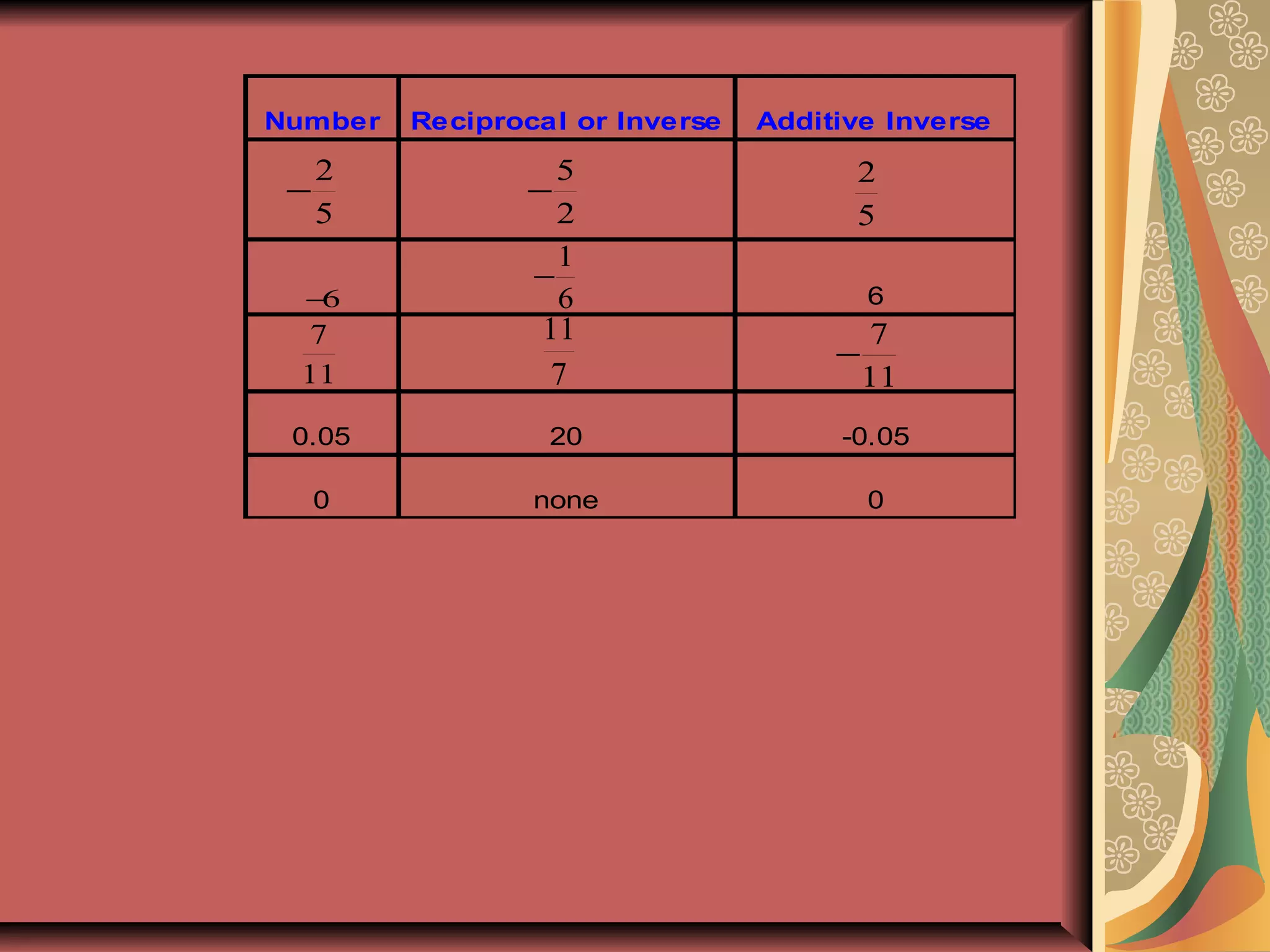
This document introduces real numbers and their properties. It discusses that real numbers can be divided into two kinds: rational numbers, which can be written as a ratio of integers, and irrational numbers, which cannot. It provides examples of rational numbers like fractions and decimals, as well as irrational numbers like square roots and pi. The document also defines integers, explains operations like exponents and identities, and illustrates the real number system.

1. Introduction to Real NumbersIntroduction to Real Numbers
andand
Their PropertiesTheir Properties

2. Two Kinds of Real Numbers
• Rational Numbers
• Irrational Numbers

3. Rational Numbers
• A rational number is a real
number that can be written
as a ratio of two integers.
• A rational number written in
decimal form is terminating
or repeating.

4. Examples of Rational
Numbers
•16
•1/2
•3.56
•-8
•1.3333…
•- 3/4

5. Irrational Numbers
• An irrational number is a
number that cannot be
written as a ratio of two
integers.
• Irrational numbers written as
decimals are non-terminating
and non-repeating.

6. Examples of Irrational
Numbers
• Square roots of
non-perfect
“squares”
• Pi
17

7. What are integers?
• Integers are the
whole numbers and
their opposites.
• Examples of integers
are
6
-12
0
186
-934

8. Using Exponents
 If “a” is a real number and “n” is a natural number, then an
=
a•a•a•••a•a (n factors of a).
where n is the exponent, a is the base, and an
is an
exponential expression. Exponents are also called powers.
To find the value of a whole number exponent:
100
= 1, 20
= 1, 80
= 1, #0
= 1
101
= 10, 21
= 2, 81
= 8, #1
= #
102
= 10 x 10 = 100, 22
= 2 x 2 = 4, 82
= 8 x 8 = 64
103
= 10 x 10 x 10 = 1000, 23
= 2 x 2 x 2 = 8
104
= 10 x 10 x 10 x 10 = 10,000 24
= 2 x 2 x 2 x 2 = 16
(-10)3
= (-10)(-10)(-10) (12).5
=

9. Using the Identity Properties
“additive identity”
 Zero is the only number that can be added to
any number to get that number.
0 is called the “identity element for addition”
a + 0 = a Example 1: 4 + 0 = 4
“multiplicative identity”
 One is the only number that can be multiplied
by any number to get that number.
1 is called the “identity element for
multiplication”
a • 1 = a Example 2: 4 • 1 = 4

10. The Real Number SystemThe Real Number SystemReal Numbers
Rational Numbers Irrational Numbers
3
1/2
-2
15%
2/3
1.456
-
0.7
0
√3 2
π
−√5
2
3π
4

11. The Real NumberThe Real Number
SystemSystem Real Numbers
Rational Numbers Irrational Numbers
31/2 -2
15
%
2/3
1.45
6
-
0.7
0
√3 2
π
−√5
2
3π
4
Integers

12. The Real Number System
Real Numbers
Rational Numbers Irrational Numbers
31/2
-2
15
%
2/3
1.45
6
-
0.7
0
√3 2
π
−√5
2
3π
4
Integers
Whole

13. The Real Number System
Real Numbers
Rational Numbers Irrational Numbers
3
1/2
-2
15
%
2/3
1.45
6
-
0.7
0
√3 2
π
−√5
2
3π
4
Integers
Whole
Natural

14. Finding Additive inversesFinding Additive inverses
 For any real number x, the number –x is theFor any real number x, the number –x is the
additive inverse of x.additive inverse of x.
Example 1:Example 1:
Number
Inverse
Additive
6 - 6
- 4 4
- 8.7 8.7
0 0
2
3
2
3
−

15. Symbol Meaning Example
= is equal to 4 = 4
≠ is not equal to 4 ≠ 5
< is less than 4 < 5
≤ is less than or equal -4 ≤ -3
> is greater than -4 > -5
≥ is greater than or equal -8 ≥ - 10

16. Number Reciprocal or Inverse Additive Inverse
−6 6
0.05 20 -0.05
0 none 0
2
5
−
5
2
−
2
5
1
6
−
11
7
7
11
7
11
−