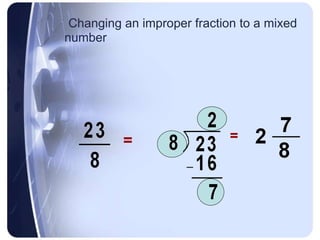
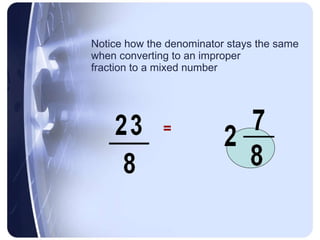
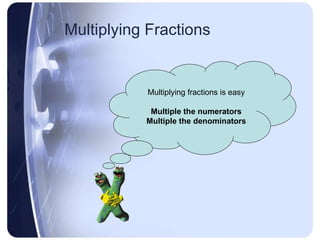
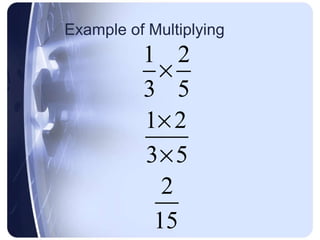
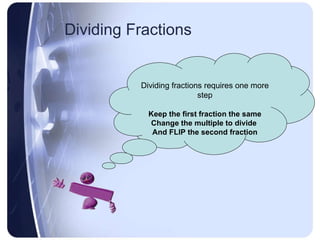
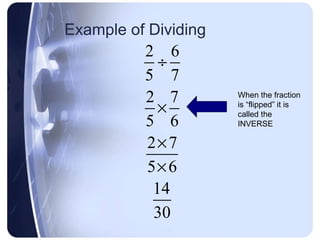
Rational numbers can be defined as any number that can be made by dividing one integer by another. This includes positive and negative numbers, whole numbers, fractions, and decimals. To add or subtract fractions, they must first be converted to have a common denominator. This is done by finding the least common multiple of the denominators and using it as the new common denominator. Multiplying and dividing fractions follows simple rules: for multiplication, multiply the numerators and multiply the denominators; for division, keep the first fraction the same, change the division symbol to multiplication, and flip the second fraction.

1. Rational Numbers Summary

2. Definition of Rational Numbers Any number that can be made by dividing one integer by another. The word comes from "ratio". This means that rational numbers include positive and negative numbers, whole numbers, fractions and decimals.

3. Two fractions that stand for the same number What is an equivalent fraction?

4. Vs. Mixed Numbers Improper Fractions

5. What is a mixed number? The sum of a whole number and a fraction

6. & These are examples of mixed numbers

7. What is an improper fraction A fraction with a numerator greater then the denominator NUMERATOR denominator

8. These are examples of improper fractions &

9. Changing an improper fraction to a mixed number = =

10. Notice how the denominator stays the same when converting to an improper fraction to a mixed number =

11. Changing a mixed number into an improper fraction = =

12. Notice how the denominators stay the same when converting from a mixed number to an improper fraction = =

13. Fractions are FUNNY!

14. Were here to show you the rules! Adding Fractions Subtracting Fractions Multiplying Fractions Dividing Fractions

15. Adding Fractions Adding fractions requires a common denominator To find the common denominator between fractions simply multiply the denominators and this is the common denominator. this number may be large so try and find a number that all denominators will divide into evenly.

16. Adding Fractions However this number may be large so try and find a number that all denominators will divide into evenly. Adding fractions requires a common denominator To find the common denominator between fractions simply multiply the denominators and this is the common denominator.

17. Example We need to find a C.D. in order to add these fractions. If we multiply the denominators that is a big number…but both 6 and 12 divide evenly (without a remainder) into 12. The first fraction already has a denominator of 12 so we leave it alone but what do we have to multiple the second denominator by in order to change it to 12? If you said 2…you are right!

18. Example continued… If you multiply the denominator by 2 you MUST multiply the numerator by two also! Remember: whatever you do to the bottom you must do to the top. Once you have common denominators…add the numerator and KEEP the Common Denominator.

19. Subtracting Fractions Same rule…you have to get a common denominator before you subtract the numerators!

20. Example of Subtraction

21. Multiplying Fractions Multiplying fractions is easy Multiple the numerators Multiple the denominators

22. Example of Multiplying

23. Dividing Fractions Dividing fractions requires one more step Keep the first fraction the same Change the multiple to divide And FLIP the second fraction

24. Example of Dividing When the fraction is “flipped” it is called the INVERSE