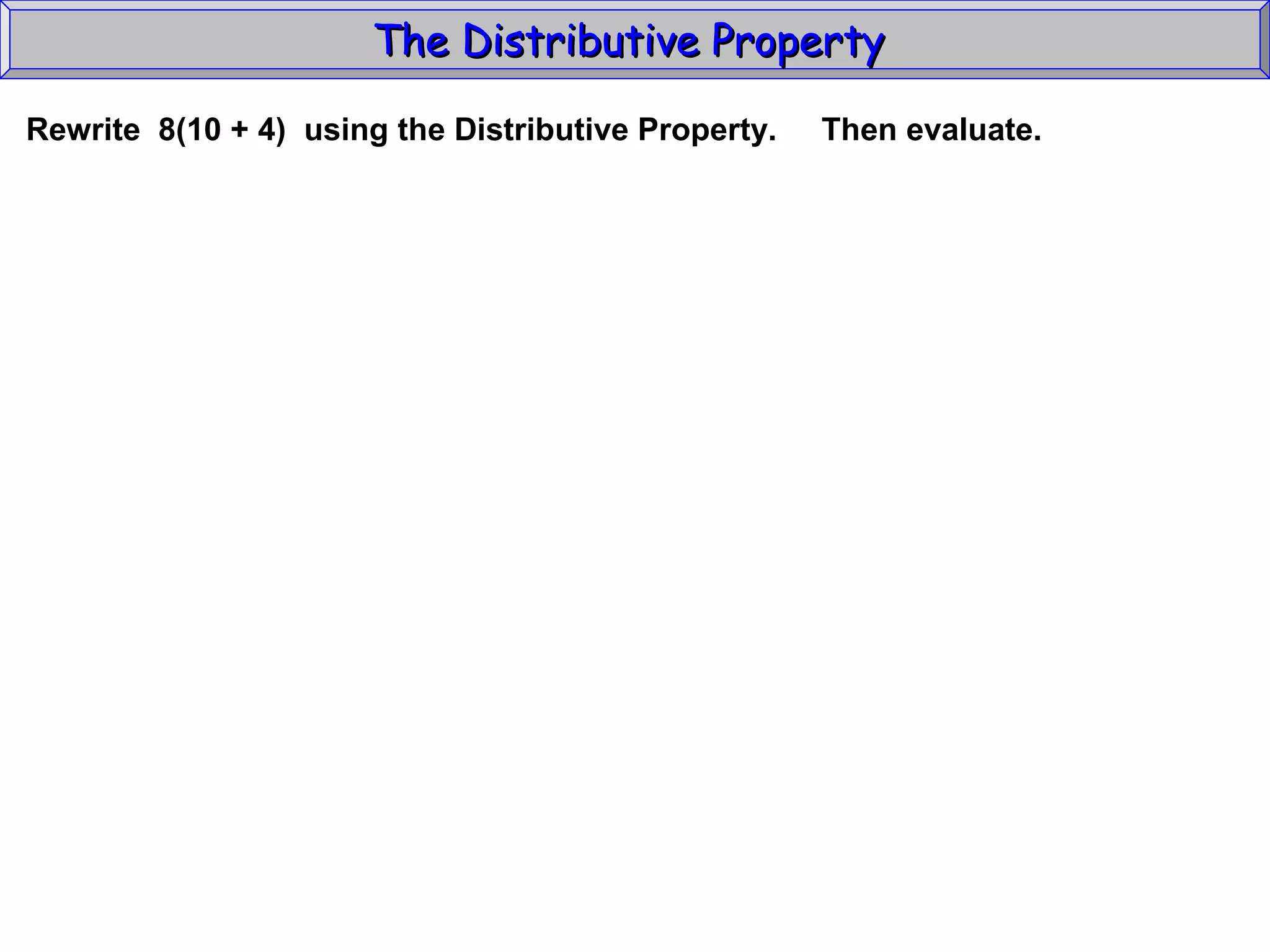
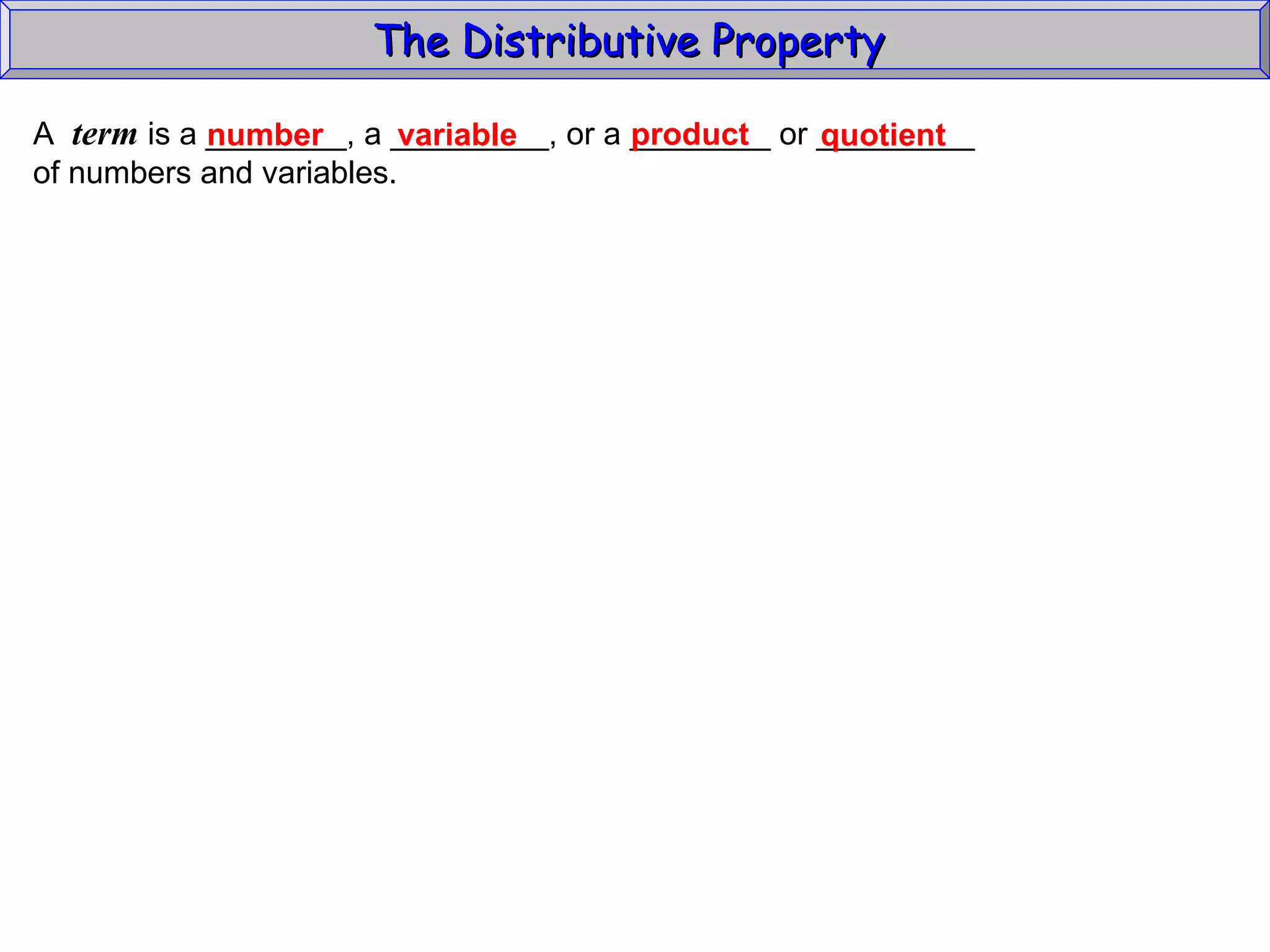
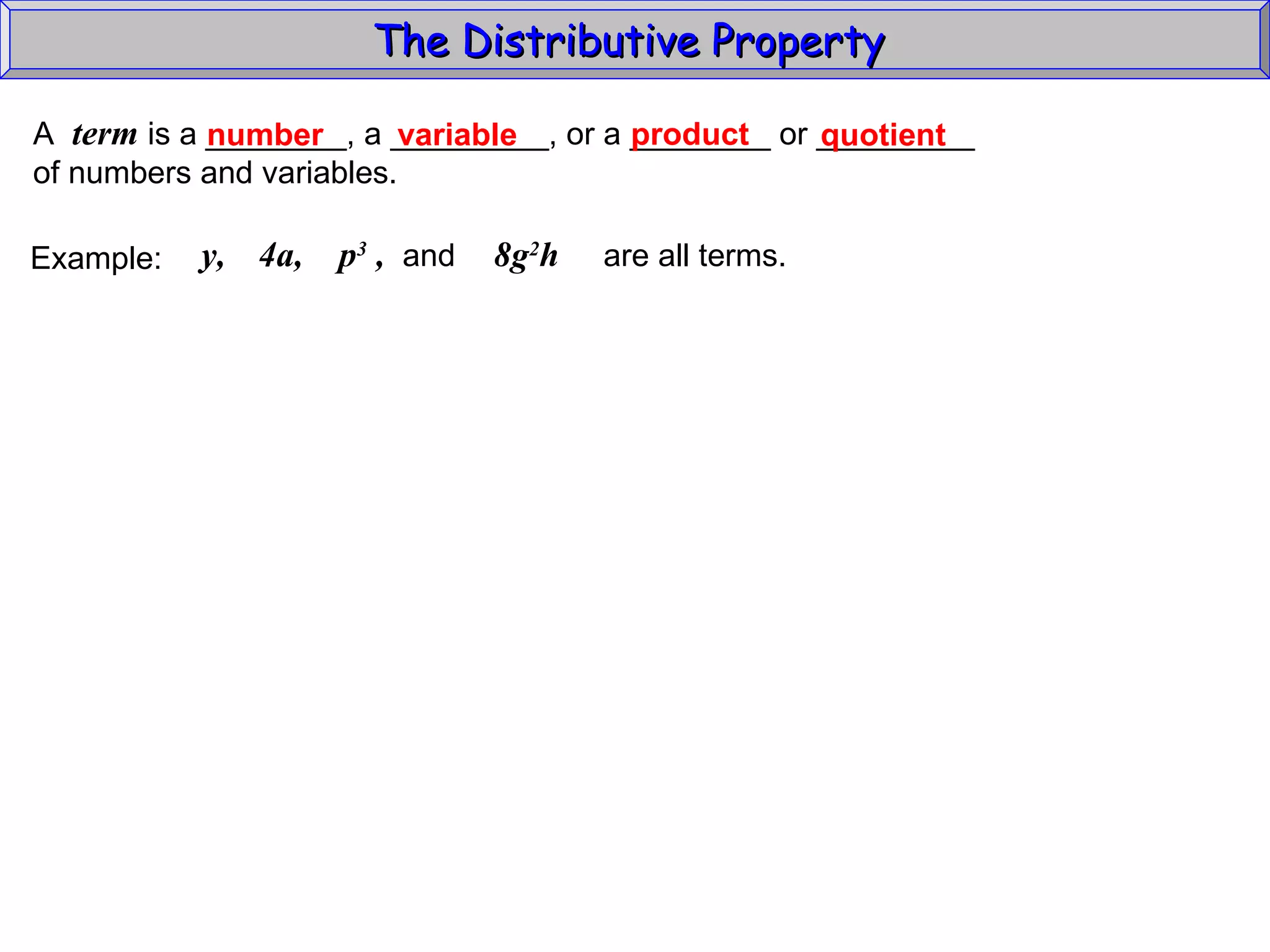
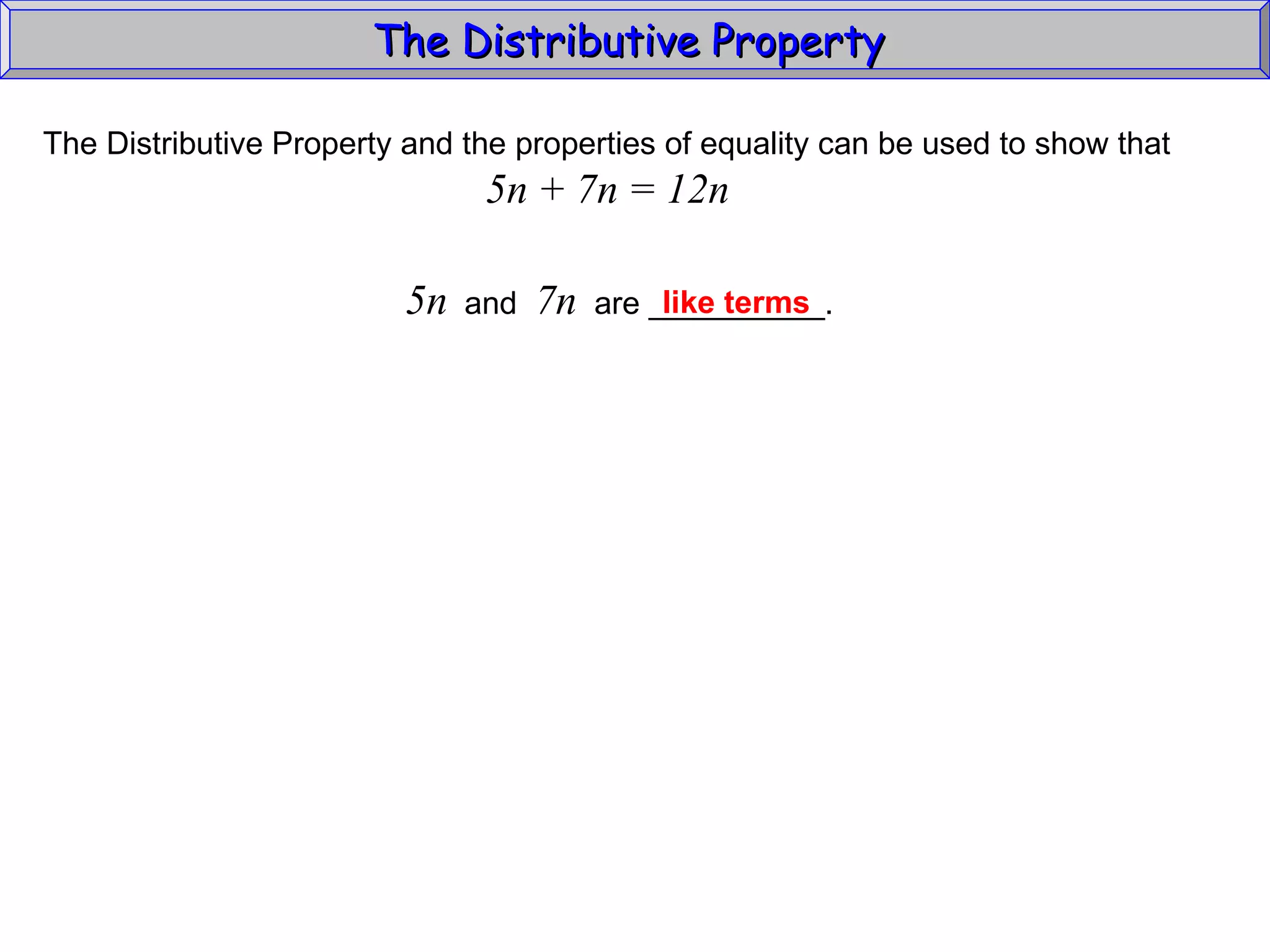
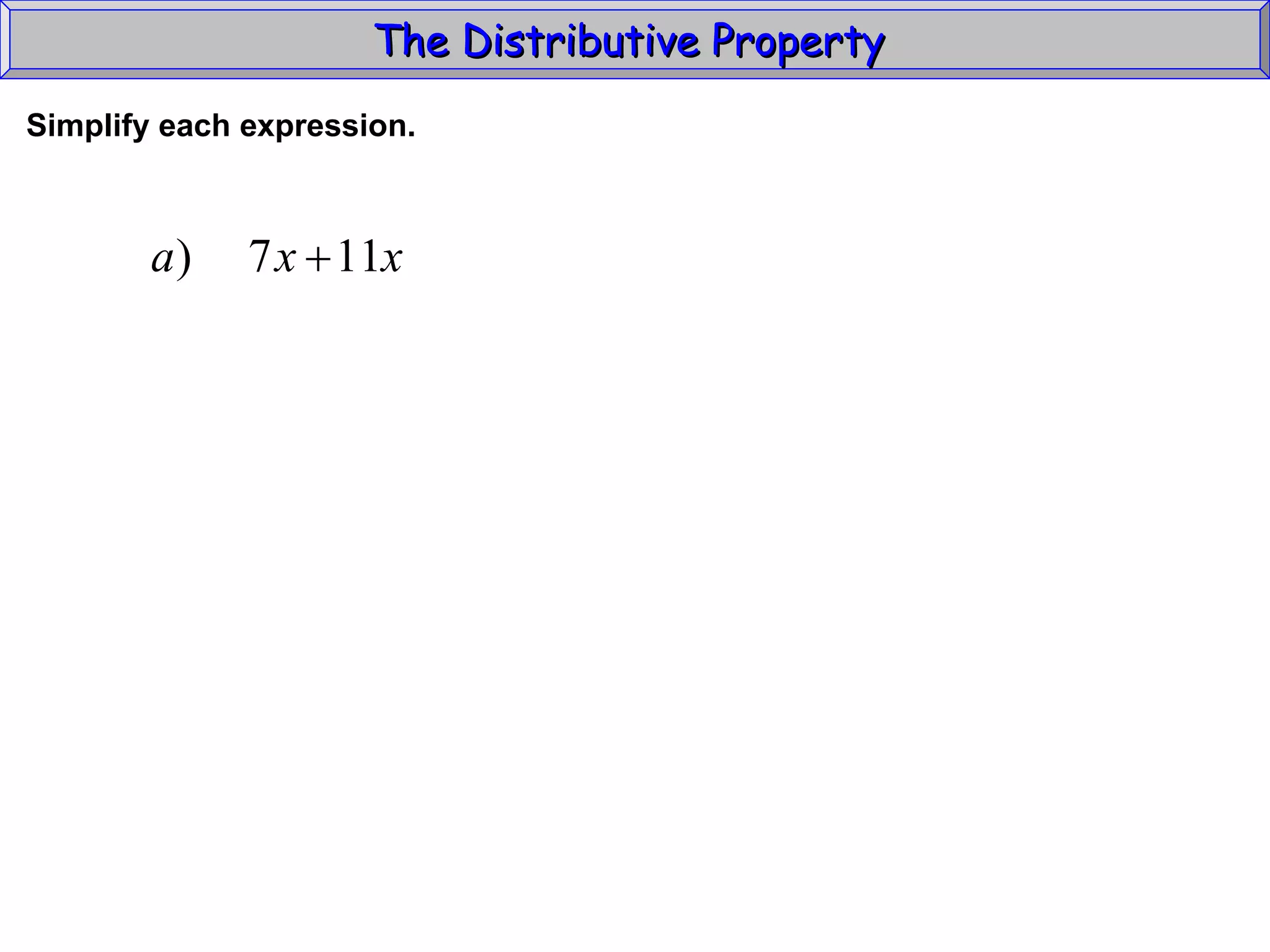
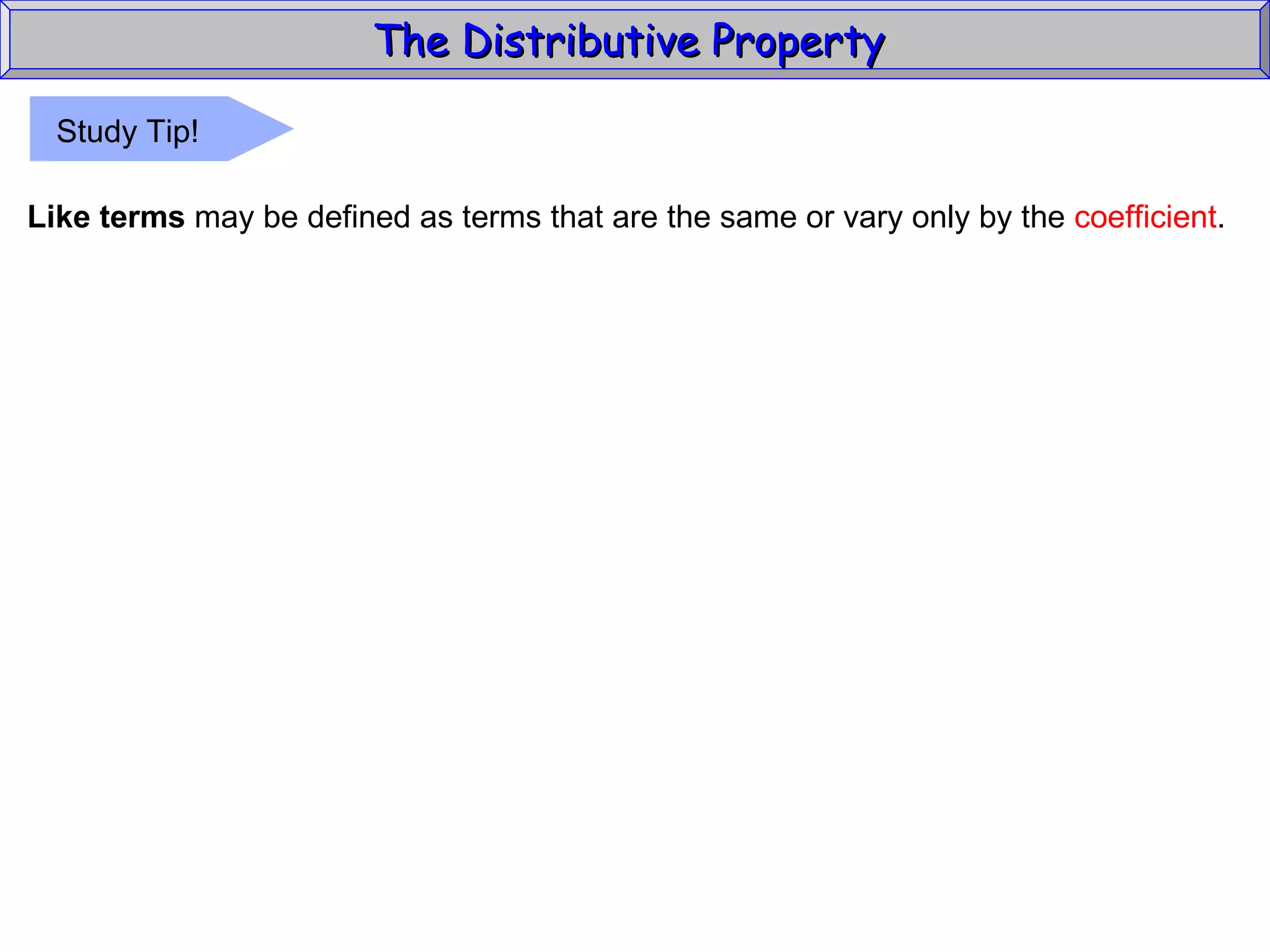
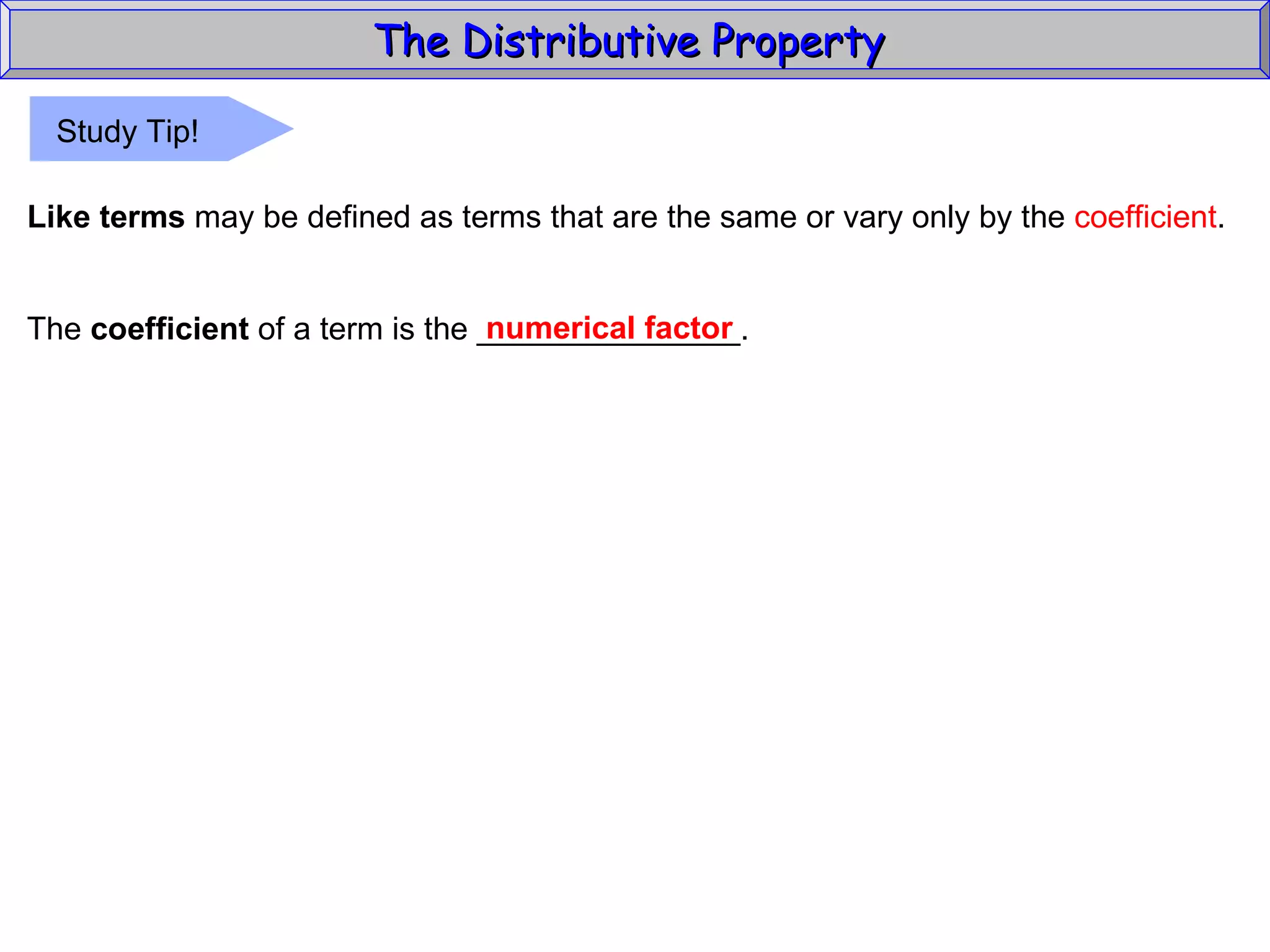
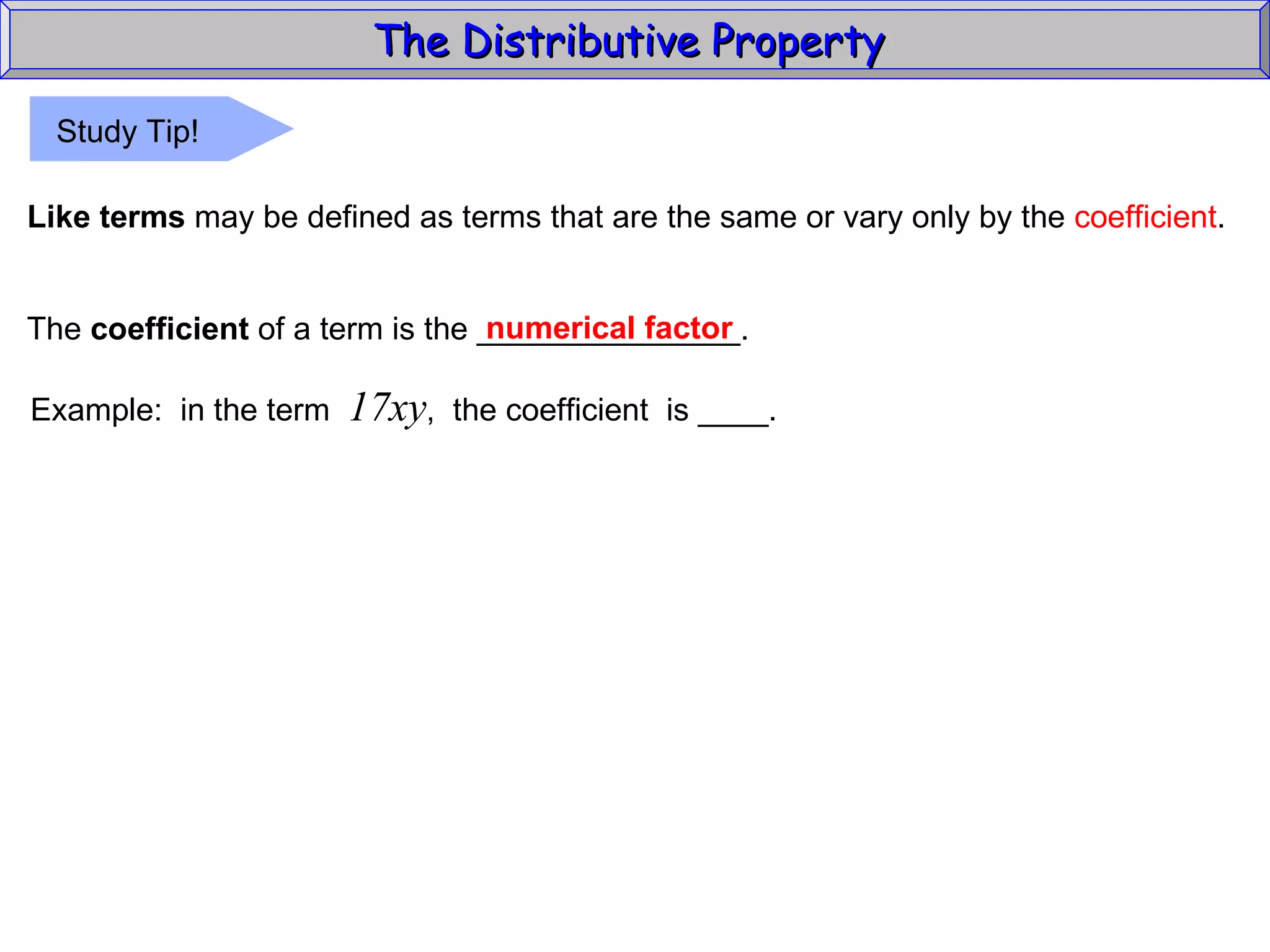
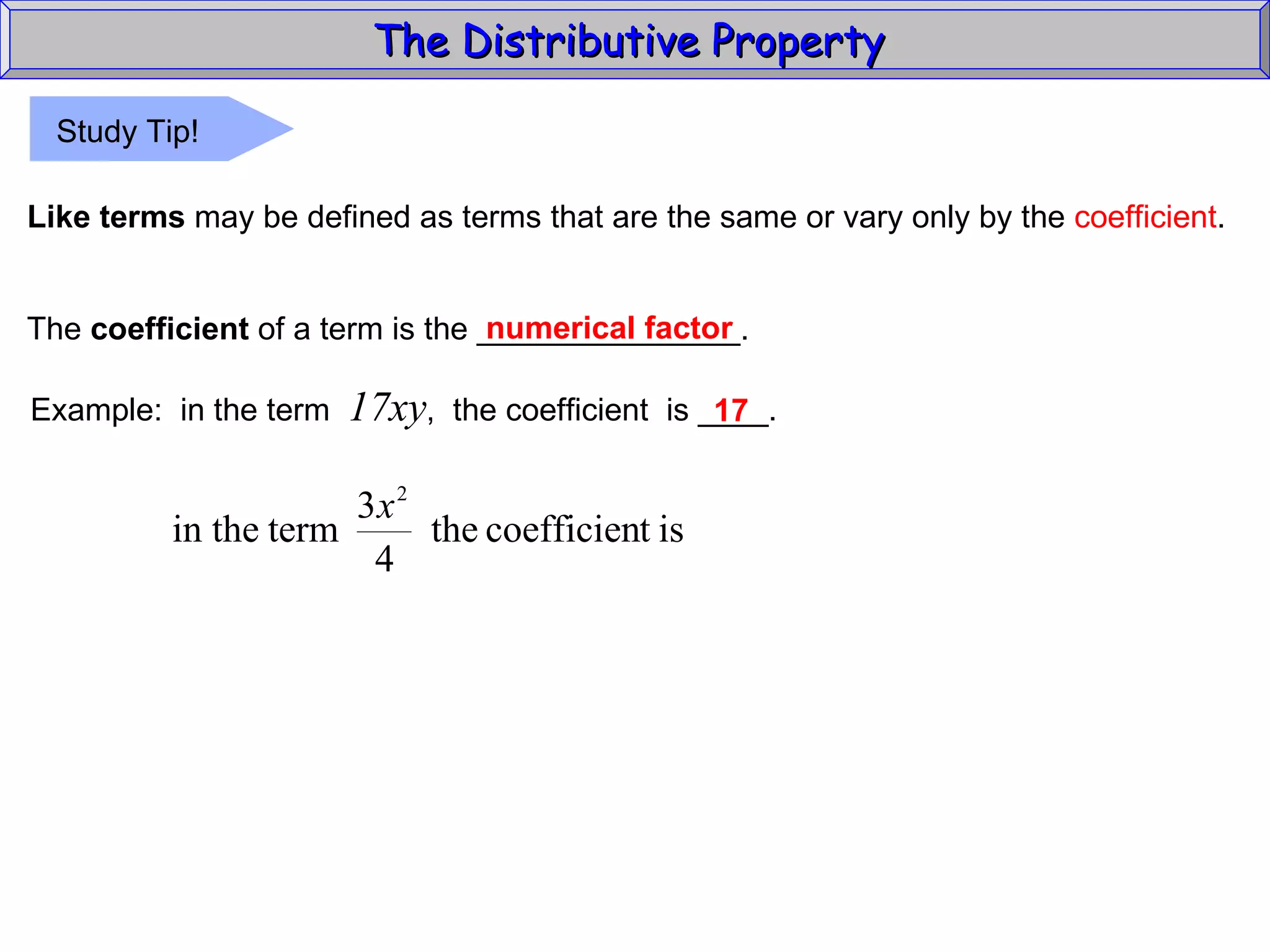
The document discusses the distributive property in algebra. It provides definitions of key terms like term, coefficient, and like terms. It gives examples of using the distributive property to simplify expressions and solve problems involving perimeter. The distributive property allows multiplying a number by the sum of two other numbers, distributing the number factor across the addition.

1. The Distributive Property

3. The Distributive Property Eight customers each bought a bargain game and a new release. Calculate the total sales for these customers.

4. The Distributive Property Eight customers each bought a bargain game and a new release. Calculate the total sales for these customers. There are two methods you could use to calculate the video game sales.

5. The Distributive Property Eight customers each bought a bargain game and a new release. Calculate the total sales for these customers. There are two methods you could use to calculate the video game sales.

6. The Distributive Property Eight customers each bought a bargain game and a new release. Calculate the total sales for these customers. There are two methods you could use to calculate the video game sales.

7. The Distributive Property Eight customers each bought a bargain game and a new release. Calculate the total sales for these customers. This is an example of the ____________________. There are two methods you could use to calculate the video game sales.

8. The Distributive Property Eight customers each bought a bargain game and a new release. Calculate the total sales for these customers. This is an example of the ____________________. Distributive Property There are two methods you could use to calculate the video game sales.

9. The Distributive Property For any numbers, a , b , and c ,

10. The Distributive Property For any numbers, a , b , and c , a ( b + c ) =

11. The Distributive Property For any numbers, a , b , and c , a ( b + c ) = ab + ac

12. The Distributive Property For any numbers, a , b , and c , a ( b + c ) = ab + ac and ( b + c ) a =

13. The Distributive Property For any numbers, a , b , and c , a ( b + c ) = ab + ac and ( b + c ) a = ba + ca

14. The Distributive Property For any numbers, a , b , and c , a ( b + c ) = ab + ac and ( b + c ) a = ba + ca a ( b – c ) =

15. The Distributive Property For any numbers, a , b , and c , a ( b + c ) = ab + ac and ( b + c ) a = ba + ca a ( b – c ) = ab – ac

16. The Distributive Property For any numbers, a , b , and c , a ( b + c ) = ab + ac and ( b + c ) a = ba + ca a ( b – c ) = ab – ac and ( b – c ) a =

17. The Distributive Property For any numbers, a , b , and c , a ( b + c ) = ab + ac and ( b + c ) a = ba + ca a ( b – c ) = ab – ac and ( b – c ) a = ba – ca

18. The Distributive Property Rewrite 8(10 + 4) using the Distributive Property. Then evaluate.

19. The Distributive Property Rewrite 8(10 + 4) using the Distributive Property. Then evaluate.

20. The Distributive Property Rewrite 8(10 + 4) using the Distributive Property. Then evaluate.

21. The Distributive Property Rewrite 8(10 + 4) using the Distributive Property. Then evaluate.

22. The Distributive Property Rewrite 8(10 + 4) using the Distributive Property. Then evaluate. Rewrite (12 – 4)6 using the Distributive Property. Then evaluate.

23. The Distributive Property Rewrite 8(10 + 4) using the Distributive Property. Then evaluate. Rewrite (12 – 4)6 using the Distributive Property. Then evaluate.

24. The Distributive Property Rewrite 8(10 + 4) using the Distributive Property. Then evaluate. Rewrite (12 – 4)6 using the Distributive Property. Then evaluate.

25. The Distributive Property Rewrite 8(10 + 4) using the Distributive Property. Then evaluate. Rewrite (12 – 4)6 using the Distributive Property. Then evaluate.

26. The Distributive Property A family owns two cars. In 1995, they drove the first car 18,000 miles and the second car 16,000 miles. Use the graph to find the total cost of operating both cars.

27. The Distributive Property A family owns two cars. In 1995, they drove the first car 18,000 miles and the second car 16,000 miles. Use the graph to find the total cost of operating both cars.

28. The Distributive Property A family owns two cars. In 1995, they drove the first car 18,000 miles and the second car 16,000 miles. Use the graph to find the total cost of operating both cars.

29. The Distributive Property A family owns two cars. In 1995, they drove the first car 18,000 miles and the second car 16,000 miles. Use the graph to find the total cost of operating both cars.

30. The Distributive Property A family owns two cars. In 1995, they drove the first car 18,000 miles and the second car 16,000 miles. Use the graph to find the total cost of operating both cars. It cost the family $15,640 to operate their two cars.

31. The Distributive Property Rewrite 4(r – 6) using the Distributive Property. Then simplify.

32. The Distributive Property Rewrite 4(r – 6) using the Distributive Property. Then simplify.

33. The Distributive Property Rewrite 4(r – 6) using the Distributive Property. Then simplify.

34. The Distributive Property Rewrite 4(r – 6) using the Distributive Property. Then simplify.

35. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables.

36. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. number

37. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number

38. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number product

39. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number product quotient

40. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number product quotient Example: y, 8g 2 h are all terms. 4a, p 3 , and

41. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number product quotient Example: y, 8g 2 h are all terms. 4a, p 3 , and Like terms are terms that contain the same _______, with corresponding variables having the same ______.

42. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number product quotient Example: y, 8g 2 h are all terms. 4a, p 3 , and Like terms are terms that contain the same _______, with corresponding variables having the same ______. variable

43. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number product quotient Example: y, 8g 2 h are all terms. 4a, p 3 , and Like terms are terms that contain the same _______, with corresponding variables having the same ______. variable power

44. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number product quotient Example: y, 8g 2 h are all terms. 4a, p 3 , and Like terms are terms that contain the same _______, with corresponding variables having the same ______. variable power

45. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number product quotient Example: y, 8g 2 h are all terms. 4a, p 3 , and Like terms are terms that contain the same _______, with corresponding variables having the same ______. variable power three terms

46. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number product quotient Example: y, 8g 2 h are all terms. 4a, p 3 , and Like terms are terms that contain the same _______, with corresponding variables having the same ______. variable power three terms

47. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number product quotient Example: y, 8g 2 h are all terms. 4a, p 3 , and Like terms are terms that contain the same _______, with corresponding variables having the same ______. variable power three terms like terms

48. The Distributive Property A term is a ________, a _________, or a ________ or _________ of numbers and variables. variable number product quotient Example: y, 8g 2 h are all terms. 4a, p 3 , and Like terms are terms that contain the same _______, with corresponding variables having the same ______. variable power three terms like terms unlike terms

49. The Distributive Property The Distributive Property and the properties of equality can be used to show that 5n + 7n = 12n 5n and 7n are __________.

50. The Distributive Property The Distributive Property and the properties of equality can be used to show that 5n + 7n = 12n 5n and 7n are __________. like terms

51. The Distributive Property The Distributive Property and the properties of equality can be used to show that 5n + 7n = 12n 5n and 7n are __________. like terms

52. The Distributive Property The Distributive Property and the properties of equality can be used to show that 5n + 7n = 12n 5n and 7n are __________. like terms The expressions 5n + 7n and 12n are called ______________________ because they denote the same number.

53. The Distributive Property The Distributive Property and the properties of equality can be used to show that 5n + 7n = 12n 5n and 7n are __________. like terms The expressions 5n + 7n and 12n are called ______________________ because they denote the same number. equivalent expressions

54. The Distributive Property The Distributive Property and the properties of equality can be used to show that 5n + 7n = 12n 5n and 7n are __________. like terms The expressions 5n + 7n and 12n are called ______________________ because they denote the same number. equivalent expressions An expression is in simplest form when it is replaced by an equivalent expression having no __________ or ____________.

55. The Distributive Property The Distributive Property and the properties of equality can be used to show that 5n + 7n = 12n 5n and 7n are __________. like terms The expressions 5n + 7n and 12n are called ______________________ because they denote the same number. equivalent expressions An expression is in simplest form when it is replaced by an equivalent expression having no __________ or ____________. like terms

56. The Distributive Property The Distributive Property and the properties of equality can be used to show that 5n + 7n = 12n 5n and 7n are __________. like terms The expressions 5n + 7n and 12n are called ______________________ because they denote the same number. equivalent expressions An expression is in simplest form when it is replaced by an equivalent expression having no __________ or ____________. like terms parentheses

57. The Distributive Property Simplify each expression.

58. The Distributive Property Simplify each expression.

59. The Distributive Property Simplify each expression.

60. The Distributive Property Simplify each expression.

61. The Distributive Property Simplify each expression.

62. The Distributive Property Simplify each expression.

63. The Distributive Property Simplify each expression.

64. The Distributive Property Simplify each expression.

65. The Distributive Property Like terms may be defined as terms that are the same or vary only by the coefficient . Study Tip!

66. The Distributive Property Like terms may be defined as terms that are the same or vary only by the coefficient . The coefficient of a term is the _______________. Study Tip!

67. The Distributive Property Like terms may be defined as terms that are the same or vary only by the coefficient . The coefficient of a term is the _______________. numerical factor Study Tip!

68. The Distributive Property Like terms may be defined as terms that are the same or vary only by the coefficient . The coefficient of a term is the _______________. numerical factor Example: in the term 17xy , the coefficient is ____. Study Tip!

69. The Distributive Property Like terms may be defined as terms that are the same or vary only by the coefficient . The coefficient of a term is the _______________. numerical factor Example: in the term 17xy , the coefficient is ____. 17 Study Tip!

70. The Distributive Property Like terms may be defined as terms that are the same or vary only by the coefficient . The coefficient of a term is the _______________. numerical factor Example: in the term 17xy , the coefficient is ____. 17 Study Tip!

71. The Distributive Property Like terms may be defined as terms that are the same or vary only by the coefficient . The coefficient of a term is the _______________. numerical factor Example: in the term 17xy , the coefficient is ____. 17 Study Tip!

72. The Distributive Property Find the perimeter of the rectangle.

73. The Distributive Property Find the perimeter of the rectangle.

74. The Distributive Property Find the perimeter of the rectangle.

75. The Distributive Property Find the perimeter of the rectangle.

76. The Distributive Property Find the perimeter of the rectangle.

77. The Distributive Property Find the perimeter of the rectangle.

78. The Distributive Property Find the perimeter of the rectangle.

79. The Distributive Property Find the perimeter of the rectangle. The perimeter of the rectangle is 28 inches .

80. Credits End of Lesson! PowerPoint created by http://robertfant.com Robert Fant