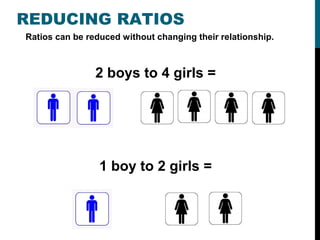
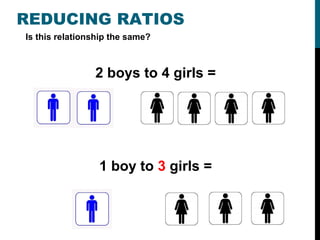
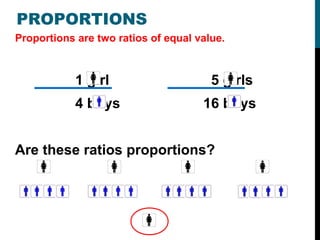
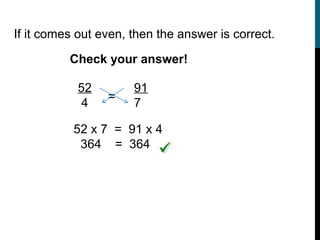
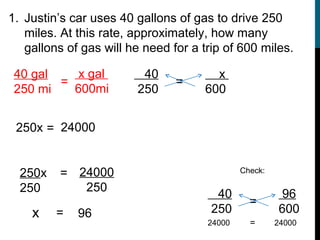
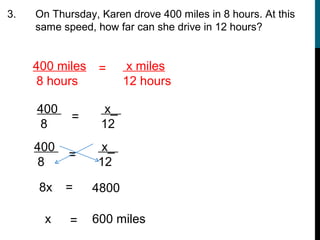
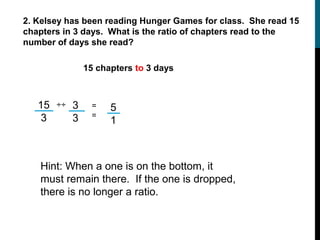This document provides instruction on ratios, proportions, and solving proportions with variables. It begins with defining ratios as comparisons between two sets of numbers and provides examples of common ratios like miles per hour. It then discusses the different ways to write ratios, such as using "to", a colon, or as a fraction. The document also covers reducing ratios, determining if two ratios form a proportion by cross-multiplying, and using proportions to solve for unknown values. Examples are provided to demonstrate setting up and solving proportions step-by-step.

1. RATIOS & PROPORTIONS
LESSON 1
TENNESSEE
ADULT EDUCATION
This curriculum was written with funding of the Tennessee Department of Labor and Workforce Development and may not be reproduced in any way without written permission. ©

2. RATIOS
Ratios are comparisons made between two sets
of numbers.
For example:
There are eight girls and seven boys in a class.
The ratio of girls to boys is 8 to 7.

3. Ratios are used everyday. They are used for:
Miles per hour
The cost of items per pound, gallon, etc.
Hourly rate of pay
80 miles to 1 hour = 80mph

4. THERE ARE 3 WAYS TO WRITE RATIOS.
1. Write the ratio using the word “to” between the two
numbers being compared.
For example: There are 8 girls and 5 boys in my class.
What is the ratio of girls to boys?
The ratio is: 8 girls to 5 boys
8 to 5

5. 2. Write a ratio using a colon between the two
numbers being compared.
For example: There are 3 apples and 4 oranges in the
basket. What is the ratio of apples to oranges?
The ratio is: 3 apples to 4 oranges.
3:4

6. 3. Write a ratio as a fraction.
For example:
Hunter and Brandon were playing basketball. Brandon
scored 5 baskets and Hunter scored 6 baskets. What
was the ratio of baskets Hunter scored to the baskets
Brandon scored?
The ratio of baskets scored was:
6 baskets to 5 baskets
6
5

7. GUIDED PRACTICE:
Directions: Write the ratio in three different ways.
There are 13 boys and 17 girls in sixth grade.
Find the ratio of boys to the girls in sixth grade.
13
13 to 17 13 : 17
17

8. RULES FOR SOLVING RATIO PROBLEMS.
1. When writing ratios, the numbers should be written in
the order in which the problem asks for them.
For example: There were 4 girls and 7 boys at the birthday
party.
What is the ratio of girls to boys?
Hint: The question asks for girls to boys; therefore, girls
will be listed first in the ratio.
4 girls
4 girls to 7 boys 4 girls : 7 boys
7 boys

9. GUIDED PRACTICE:
Directions: Solve and write ratios in all three forms.
1. The Panthers played 15 games this season. They won 13
games. What is the ratio of games won to games played?
The questions asks for Games won to Games
played.
13
13 to 15 13:15
15

10. 2. Amanda’s basketball team won 7 games and lost 5.
What is the ratio of games lost to games won?
THE QUESTION ASKS FOR GAMES LOST TO GAMES
WON. THEREFORE, THE NUMBER OF GAMES LOST
SHOULD BE WRITTEN FIRST, AND THE GAMES WON
SHOULD BE WRITTEN SECOND.
Games lost = 5 to Games won = 7
5 to 7 5:7 5
7

11. REDUCING RATIOS
Ratios can be reduced without changing their relationship.
2 boys to 4 girls =
1 boy to 2 girls =

12. REDUCING RATIOS
Is this relationship the same?
2 boys to 4 girls =
1 boy to 3 girls =

13. 2. ALL RATIOS MUST BE WRITTEN IN
LOWEST TERMS.
Steps:
1. Read the word problem.
2. Set up the ratio.
For example:
You scored 40 answers correct out of 45 problems on a
test. Write the ratio of correct answers to total questions in
lowest form.
Step 1: Read the problem. What does it want to know?
40 to 45 40 : 45 40
45

14. 3. Reduce the ratio if necessary.
Reduce means to break down a fraction or ratio into the
lowest form possible.
Reduce = smaller number; operation will always be division.
HINT: When having to reduce ratios, it is better to set up the ratio in the
vertical form. (Fraction Form)
40
40 to 45 =
45
Look at the numbers in the ratio. What ONE
number can you divide BOTH numbers by?
Factors of 40: 1, 2, 4, 5, 8, 10, 20, 40
Factors of 45: 1, 3, 5, 9, 15, 45 40 ÷ 5 = 8
45 ÷ 5 = 9

15. Guided Practice:
Directions: Solve each problem. Remember to reduce.
1. There are 26 black cards in a deck of playing cards. If there are 52 cards
in a deck, what is the ratio of black cards to the deck of cards?
Step 1: Read the problem. (What does it want to know?)
Step 2: Set up the ratio.
26 black cards to 52 cards
Step 3: Can the ratio be reduced? If so, set it up like a fraction.
26 ÷ 26 = 1
52 ÷ 26 = 2
What is the largest number that will go into
both the top number and the bottom number
evenly? (It can not be the number one!)

16. 2. Kelsey has been reading Hunger Games for class. She read 15
chapters in 3 days. What is the ratio of chapters read to the
number of days she read?
15 chapters to 3 days
15 ÷÷ 3 = 5
3 3 =
1
Hint: When a one is on the bottom, it
must remain there. If the one is dropped,
there is no longer a ratio.

17. PROPORTIONS
Proportions are two ratios of equal value.
1 girl 4 girls
4 boys 16 boys
Are these ratios saying the same thing?

18. PROPORTIONS
Proportions are two ratios of equal value.
1 girl 5 girls
4 boys 16 boys
Are these ratios proportions?

19. DETERMINING TRUE PROPORTIONS:
To determine a proportion true, cross multiply.
If the cross products are equal, then it is a true proportion.
4 = 20
5 25
20 x 5 = 4 x 25
100 = 100
The cross products were equal, therefore 4 And 20 makes a true proportion.
5 25

20. Guided Practice:
Directions: Solve to see if each problem is a true proportion.
1. 3 = 15
5 25
2. 6 = 57
8 76
3. 7 = 37
12 60

21. Guided Practice:
Directions: Solve to see if each problem is a true proportion.
3 15 6 57
1. 5 = 25 2. = 3. 7 = 37
8 76 12 60
15 x 5 = 3 x 25 57 x 8 = 6 x 76
7 x 60 = 37 x 12
456 = 456
75 = 75 420 = 444
true true
false

22. SOLVING PROPORTIONS WITH VARIABLES
What is a variable? A variable is any letter that takes place of a
missing number or information.
Eric rode his bicycle a total of 52 miles in 4 hours. Riding at
this same rate, how far can he travel in 7 hours?
Next, the problem states “how
far can he travel in 7 hours.
Look for the two sets of You have 52 miles in 4
The problem is missing the
ratios to make up a hours. This is the first
miles. Therefore, the miles
proportion. ratio.
becomes the variable.
Set 1 52 miles n miles
Set 2
4 hours 7 hours
The proportion should be 52 = n
4 7
set equal to each other.
HINT: The order of the ratio does matter!

23. SOLVING THE PROPORTION:
When solving proportions, follow these rules:
1. Cross multiply.
2. Divide BOTH sides by the number connected to the variable.
3. Check the answer to see if it makes a true proportion.
Problem: 52 n
=
4 7
4 x n = 52 x 7
Which number is
connected to the variable? 4n = 364 n = 91 miles
4 4
Since the 4 is connected
to the variable, DIVIDE
both sides by the 4.
4 ÷ 4 = 1; 364 ÷ 4 = 91
therefore you
are left with “n”
on one side.

24. If it comes out even, then the answer is correct.
Check your answer!
52 91
=
4 7
52 x 7 = 91 x 4
364 = 364

25. GUIDED PRACTICE
Directions: Solve each proportion.
1.For every dollar Julia spends on her Master
Card, she earns 3 frequent flyer miles with
American Airlines. If Julia spends $609 dollars on
her card, how many frequent flyer miles will she
earn?

26. GUIDED PRACTICE
Directions: Solve each proportion.
1. For every dollar Julia spends on her Master Card, she
earns 3 frequent flyer miles with American Airlines. If Julia
spends $609 dollars on her card, how many frequent flyer
miles will she earn?
Step 1: Set up the proportion. $1.00 = $609.00
3 miles d miles
Step 2: Cross multiply.
1d = 1827
Step 3: Divide
1 1
Step 4: Check answer. d = 1827

27. 1. Justin’s car uses 40 gallons of gas to drive 250
miles. At this rate, approximately, how many
gallons of gas will he need for a trip of 600 miles.
2. If 3 gallons of milk cost $9, how many jugs can
you buy for $45?
3. On Thursday, Karen drove 400 miles in 8 hours.
At this same speed, how far can she drive in 12
hours?

28. 1. Justin’s car uses 40 gallons of gas to drive 250
miles. At this rate, approximately, how many
gallons of gas will he need for a trip of 600 miles.
40 gal x gal 40 x
= =
250 mi 600mi 250 600
250x = 24000
250x = 24000 Check:
250 250
40 96
=
x = 96 250 600
24000 = 24000

29. 2. If a 3 gallon jug of milk cost $9, how many 3
gallon jugs can be purchased for $45?
1 n
=
9 45
Check:
1= n
9 45 1 5
9 =
45
1x45 = 9n
45 = 45
45 = 9n
9 9
5=n
5 jugs of milk can be
purchased for $45

30. 3. On Thursday, Karen drove 400 miles in 8 hours. At this
same speed, how far can she drive in 12 hours?
400 miles = x miles
8 hours 12 hours
400 x_
=
8 12
400 x_
=
8 12
8x = 4800
x = 600 miles

31. 4. Susie has two flower beds in which to plant tulips and
daffodils. She wants the proportion of tulips to daffodils to be
the same in each bed. Susie plants 10 tulips and 6 daffodils in
the first bed. How many tulips will she need for the second bed
if she plants 15 daffodils?
10 tulips = x tulips 10 x_
=
6 daffodils 15 daffodils 6 15
10 x x = 25 tulips
=
6 15
6x = 150 10 25
=
6x 150 6 15
=
6 6 150 = 150
x = 25